INTRODUCTION
Light impinging on the snow surface in a collimated beam is reflected diffusely into the upper hemisphere. That this reflection is not isotropie but prefers certain directions is often seen with the unaided eye, and can be measured by fairly simple techniques. Measurements of this kind furnish an important boundary condition for the computation of radiative transfer through the atmosphere. They give, to some extent, an indication of the structure of the snow surface and may thus serve as a means of remote sensing. Finally, the anisotropy of reflection modifies the calibration factor of most hemispheric pyranometers used for determining the albedo of snow.
Little has been published about measurements of the bidirectional reflectivity of snow (Middleton and Mungali 1952; Griggs and Marggraf 1967 as quoted in Warren 1982; and O’Brien and Munis 1975) or the
hemispherical-directional reflectivity (Salomonson and Marlatt 1968; Dirmhirn and Eaton 1975; Kuhn 1974). The hemispherical reflectivity of snow, on the other hand, has often been investigated as a function of solar elevation (for summaries see Kuhn and others 1977; Warren 1982).
The present paper discusses the geometry of reflection and types of reflectivity. Examples of hemispherical-directional and of bidirectional reflectivities are presented that were measured at various wavelengths using solar radiation as a source in Antarctic locations, and an Argon laser for measurements on alpine snow.
THE GEOMETRY OF REFLECTION
Since snow is not specularly reflecting, four angles are needed to describe the position of incident and reflected rays, as shown in Figure 1: the solar zenith angle Θ, solar azimuth φ, zenith angle θr, or elevation hr of the reflected ray, and its azimuth φΓ. As long as the snow structure has a preferred azimuth (notably due to sastrugi or ripples at the surface) φ and φΓ have to be retained; if the snow structure is isotropie with respect to the azimuth angle, only (Φ - Φ) is relevant. In this paper, the azimuth circle was fixed with respect to the sun: φ = 0 at the solar azimuth, asymmetries appearing in many of the diagrams testify to irregular surface structures.
In order to describe the transfer of radiant energy at the snow surface, let J = incident radiance (intensity) in Watt per square meter normal to the direction of propagation, per steradian; R = reflected radiance (W m-2sr-1);. Fi = irradiance of a plane surface of arbitrary orientation (W m-2); Fr = radiant power reflected per unit surface area (W m-2);) F↟, F?, = corresponding irradiance and reflectance of a horizontal surface. Fi can be converted into F? if a, θ Φ, the normal vector of the surface, and the reflectivity and orientation of that part of the surface obstructing the sky are known.

Fig. 1. Reflection geometry. I incident, R reflected radiance (energy per time, per area normal to the direction of propagation, per solid angle), θ, ΘΓ zenith angle; Φ, ΦΓ azimuth angle of incident and reflected ray, respectively.
DiF. = J(Θ, φ) cose dΩ
Ω being the solid angle
d2Ω = sine dΘ d Φ
Consequently

and analogously

In general treatments of the energy balance of snow surfaces, the ratio of upward to downward flux is called the albedo.
In this paper the following distinctions will be made in accordance with Siegel and Howell (1968):
-
1) hemispherical reflectivity ρ = Fr/Fi
-
2) hemispherical-directional reflectivity ρi
The reference to the solid angle is necessary for the comparison of measurements with instruments of different aperture. In the experiments described in this paper, neither the detector nor the reflecting snow surface are point sources which means that only vaguely defined ‘effective’ solid angles can be given. For this reason, among others, ρ1 values will be normalized to the aximuth of maximum radiance so that the solid angle increment cancels.
-
3) bidirectional reflectivity
where R” contains only that part of the energy that originates from J(θ, Φ). (In general, R is contributed to by diffuse radiance from all directions of the hemisphere, while R” is the radiance of the reflected direct solar beam. As with ρ1, the reference to the solid angle in ρ” is dropped after normalization.
THE DIFFUSE COMPONENT OF IRRAD1ANCE
In nature a true case of bidirectional reflectivity am be observed only when all incident energy is concentrated in a single point source, eg the sun. Measurements at three Antarctic locations have confirmed theoretical expectations that this situation is approached to better than 10% in the near infrared at about λ > 800 nm, whereas nearly all incident energy is diffuse at the lower end of the visible spectrum.
The values in Figure 2 were determined by shading the direct solar radiance from the receiving head of a spectrometer in order to measure diffuse irradiance only. since this setup was not very elaborate and since the geometry of the receiver was not known in sufficient detail, the effective angle subtended by the shading disc can only approximately be stated as 15 deg in diameter.

Fig. 2. Ratio of diffuse to global irradiance at clear sky, vs wavelength, for three antarctic stations, with respective solar elevations.
It is obvious that the diffuse fraction of irradiance increases with the total amount of scattering particles above the point of observation: South Pole at the level of 700 hPa has a considerably darker sky than McMurdo at sea level (1000 hPa).
SPECTRALLY INTEGRATED REFLECTIVITY AT PLATEAU STATION
In the austral summer 1968/69 a Linke-Feussner pyrheliometer (by K.ipp and Zonen) was installed on top of the 32 m high tower of Plateau Station. It has an aperture of 11 deg diameter and a spectrally uniform receiver covered by a quartz filter transmitting from 350 to 4000nm.
The tube was tilted at 5, 15, and 25 deg below the horizon and moved through the azimuth indicated on Figure 3. Values shown are normalized by R(Φ, θ)/R(0, θ). As it took about 20 minutes to record one set of values, the solar elevation did not change appreciably and the data represent values of normalized, spectrally integrated, hemispherical-directional reflectivity.

Fig. 3. Spectrally integrated (350 = 3700 nm) reflected radiance, normalized by R(Θr, φr)/R(Θrγ/0), at Plateau Station, for indicated solar zenith angles e and reflection angles Θr.
Plateau Station is situated at 80 °S, 40°E, 3625 m, with 610 hPa mean station pressure, and is characterized by summer temperatures lower than -20°C. The snow surface is gently carved by sastrugi of less than 50 cm height, and has slopes of the order of 10-3 with mean density 300 -400 kg m-3.
The data in Figure 3 show effects that will be found similarly in monochromatic measurements at other polar and alpine stations:
1) A reflectance peak at the solar azimuth which becomes more pronounced when the horizon is approached
2) An enhancement of this effect at high solar zenith angles.
MONOCHROMATIC REFLECTIVITY MEASUREMENTS AT SOUTH POLE AND OTHER ANTARCTIC SITES
South Pole station is situated at 2800 m, with 700 hPa mean station pressure, and summer temperatures generally below -10°C. Mean wind speeds are higher than at Plateau Station, but in the vicinity of the station, the surface is somewhat smoother due to the aerodynamic influence of the buildings.
The data were measured with an ISCO spectrometer of 15 nm half width in the visible and 25 nm in the near infrared part of the spectrum. The instrument was equipped with a 2n diffuser disc mounted on a 1 m light pipe which remained flexible at all temperatures encountered. The diffuser disc was fitted with an aluminium tube coated with Parson’s Black and having an aperture of 5° diameter.
Data in Figure 4 are comparable in their measuring geometry to the Plateau data but are averages of two records at 750 nm and one at 1000 nm, which renders them nearly bidirectional. Again the values shown are normalized by R(θr/Φr/R θr/0). They were made symmetric to _ the sun’s vertical by averaging left and right azimuth points. The mean values thus gained are to a good extent free from the influence of 0.1 - 10 m scale surface features.
The upper part of Figure 4 contains data recorded from the roof of the clean air building at South Pole Station and represents a snow surface modified by minor drift and increased accumulation. The data in the lower part of Figure 4 were taken about 1 km upwind from the station, where the natural surface is less smooth. While the curves for θΓ = 87° are nearly congruent, there is a distinctly different shape in the curves for θΓ = 70 . whether this effect, however small, is due to surface roughness alone or also to contamination of the snow needs to be further investigated.
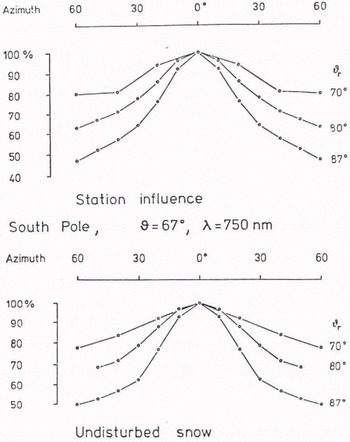
Fig. 4. Reflected radiance at 750 nm, normalized by R(θr, Φr )/R(Φr,0), at South Pole. Upper part over snow in the immediate vicinity of station buildings, lower part 1 km upwind of the station. Each diagram represents the average of three records in which left and right azimuth were averaged as well.
Comparison of Figures 3 (θo = 68?) reveals a striking difference: at comparable solar zenith angle, the anisotrophy at Plateau Station is much in excess of that at South Pole. There are two facts that may be involved, one is that Plateau data are spectrally integrated (350 -3700 nm) whereas South Pole data in Figure 4 are averages of three records, two at 750 nm and one at 1000 nm. The second is the grain size of the respective snow covers: at Plateau Station, the surface was old, metamorphized and partly wind crusted, whereas snow of the South Pole data was fresh and of finer grain.
In Figure 5 data have not been normalized but are given in arbitrary units of radiance. A third characteristic of subsolar reflectance shows very clearly, viz. the respective brightening or darkening of the horizon close to or distant from the solar azimuth. In the solar azimuth (φγ = 0) the reflected radiance increases with ΘΓ so that the snow immediately below the horizon (Θr = 87°) appears brighter than, for example, at Θ r = 70°. At azimuth angles farther than 30° away from the solar azimuth, the situation is reversed and the horizon appears darker. The same effect is obvious in Figure 6 and was observed at Plateau Station as well.
In Figure 6 the wavelength enters as a new variable (λ, θ, θr Φ – ΦΓ)- The effects just described are more pronounced at 750 ‘and 1000 nm than at 450 nm where the natural conditions are not so close to bidirectional reflection.
Judged by the predominance of the diffuse over the direct component of irradiance at 450 nm indicated by

Fig. 5. Reflected radiance at 750 nm in arbitrary units of energy per time, per area normal to the direction of propagation, per solid angle. Measurements near buildings = Pole station.
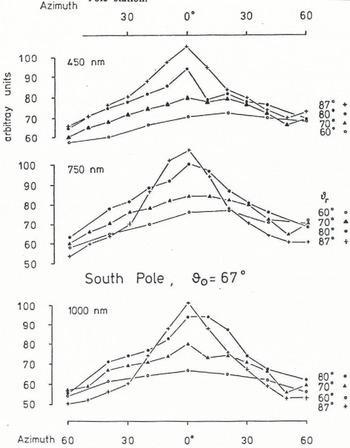
Fig. 6. Reflected radiance at three wavelengths, in arbitrary units of energy per time, per area normal to the direction of propagation, per solid angle. Measurements 1 km upwind of South Pole station.
Figure 2, it is surprising to note how well developed the subsolar maximum is at that wavelength in Figure 6. One should bear in mind, however, that much of the diffuse irradiance is still originating from the circumsolar region under antarctic conditions. For instance, measurements at Plateau Station (Figure 4 in Kuhn and others 1977) indicated that at solar zenith angle Θ = 55° J(Θ - 55, φ = 30) is still three times as high as J(Θ = 55, Φ = 60). Apart from the illustration of spectral changes of directional reflectivity, Figures 5 and 6 demonstrate the influence of the surface structure which in some cases makes R(Φ r = 10) exceed R(Φ = 0) and introduce other irregularities in R(Φr, O). In this respect measurements at South Pole were inferior to those from the tower at Plateau Station, since at South Pole the measuring platform was either 6 m above ground on the roof of the clean air building, or only 1.5 m at outlying locations, which yields a comparably small field of view.
The pattern of reflectivity remained essentially the same when snow fields at McMurdo Sound were investigated. In the case of Figure 7 the surface was rippled by wind action, and temperature was close to 0°C so that larger grain sizes than at South Pole must be assumed. Figure 7 contains two scans around the horizon at 500 and 900 nm, respectively, which display a broad subsolar peak and a weak secondary maximum most likely due to retro-reflection at ΘΓ = -θ.
Measurements over bare ice at Canada Glacier in Taylor Valley, Antarctica, are reproduced in Figure 8, Although glacier ice has a much coarser structure than snow the behaviour of the reflectance pattern was basically the same. At 1000 nm wavelength and Θr = 85°, the ratio of maximum radiance at φγ = 0 to the radiance at φΓ = 45° is 1.5, in the case of Figure 7 (er = 30°at 900 nm) it was 1.3 and 1.5 for the respective left and right azimuth, whereas at South Pole (Figure 6, 1000 nm, θΓ = 87°) it was 1.8

Fig. 7. Reflected radiance at selected wavelengths over slightly windblown snow on McMurdo Sound. Values are normalized by R(θr, Φr)/R(θr, O).

Fig. 8. Reflected radiance at 450 and 1000 nm, in arbitrary units of energy per time, per area normal to the direction of propagation, per solid angle, over bare ice on the tongue of Canada Glacier, Taylor Valley, Antarctica.

Fig. 9. Reflected radiance of an Argon-ion laser beam at 514 nm over alpine snow. Values are normalized by R(θr,)R(Φr, O). Note importance of incidence angle and insensitivity to the two types of snow.
LASER MEASUREMENTS ON ALPINE SNOW
In order to obtain records of true bidirectional reflectivity also in the visible part of the spectrum the beam of an Argon-ion laser with λ = 514 nm was directed at the snow cover outside the laboratory at Davos, Switzerland. Figure 9 shows two pairs of θ, ΘΓ which again demonstrate the reflectance peak. As in McMurdo (Figure 7), a weak maximum was observed at φΓ = 180 . Compared to Plateau, South Pole and McMurdo the peak was sharper under laser illumination: at Θ = 70°, ΘΓ = 73°, Φr = 60° the radiance had only 50% of its peak value whereas at South Pole (Θ = 68°, ΘΓ, = 70°, φΓ = 60°) this fraction was between 70 and 80%, most likely due to the diffuse irradiance. It is interesting to note that at Davos cold, fine powder snow and fresh, fine-grained, but wet snow yielded the same results. Measurements on coarse snow in spring showed the anisotropy increasing with grain size.
CONCLUSIONS
Measurements of the reflectance distribution of polar and alpine snow display a reflectance peak in the solar azimuth direction which is essentially contained within φγ 60°. This peak is better developed with large incidence angles Θ, large reflectance angles ΘΓ, and larger grain size. Under natural irradiance the diffuse component dominated in the blue and becomes insignificant in the near infrared spectral region, which makes the reflectance peak increase with wavelength in the case of hemispherical-directional reflectivity. Laser measurements of truly bidirectional reflectivity of alpine snow at 514 nm, however, yielded reflectance peaks comparable to those measured on polar snow at 750 and 1000 m.
ACKNOWLEDGEMENTS
The polar part of this research was sponsored by the Office of Polar Programs, NSF, Washington DC, the alpine part by the Austrian Academy of Sciences. Thanks are due to Leonide; Siogas for help in the Antarctic field work.











