1) Introduction
In seeking quantitative descriptions of glacier flow, attention is generally limited to glaciers which are either cold or temperate. With the exception of Reference FowlerFowler (1979[b]) and Reference Hutter and OlunloyoHutter and Olunloyo (1980) there are no investigations known to us which deal with the state of stress and velocity in a polythermal environment. Such glaciers are partly temperate and partly cold, and, depending on which of these states applies at the base, the ice is thought to be either fully adhering or sliding over its bed. It does not seem to be necessary to defend the postulate of the existence of poly thermal glaciers, as there is sufficient field evidence corroborating cold ice in glaciers that are believed to be temperate at their beds. Reference HarrisonHarrison (1972) reports that water in some bore holes slowly freezes; Reference TheakstoneTheakstone (1967) mentions that air temperatures in a tunnel beneath 50 m of ice near the margin of Østerdalsisen in Norway remained almost constant at -0.1 °C, and Reference Vivian and BocquetVivian and Bocquet (1973) state that the ice roof of natural subglacial caverns in the Glacier d'Argentiere was often below the melting point.Reference Robin and deRobin (1976) has offered a “heat pump” argument to explain the existence of cold patches at the base of a temperate glacier. It appears that spatial, as well as temporal, variations of basal pressure cause freezing of ice to rock. Indirect evidence in support of this is the intermittent stick-slip motion of temperate glaciers reported by both Reference TheakstoneTheakstone (1967) and Reference Vivian and BocquetVivian and Bocquet (1973).
The cold patches at the base, described by Reference Robin and deRobin (1976), are assumed to be of the extent of the roughness amplitudes of the bed, or smaller, and must therefore affect the viscous sliding law supposed to apply at the smoothed-out surface of the global flow problem; in a first approximation, one may assume that they only affect the constant C in the sliding law
where u
b is the basal sliding velocity, τ the corresponding shear traction, and C and m are constants, m having the value  (Reference LliboutryLliboutry 1979, Reference WeertmanWeertman 1979) or n (Reference FowlerFowler 1979[a]), n being the exponent in Glen's flow law. A proper treatment would have to take into account possible stress concentrations at the separation lines of cold and temperate ice and would have to include the possibility of tearing off some rocks from below. A mathematical solution to this problem does not seem to be in sight as it would consist of a complex, mixed boundary value problem.
(Reference LliboutryLliboutry 1979, Reference WeertmanWeertman 1979) or n (Reference FowlerFowler 1979[a]), n being the exponent in Glen's flow law. A proper treatment would have to take into account possible stress concentrations at the separation lines of cold and temperate ice and would have to include the possibility of tearing off some rocks from below. A mathematical solution to this problem does not seem to be in sight as it would consist of a complex, mixed boundary value problem.
However, when the cold and temperate portions of the base extend over several thicknesses of the glacier, the stress-concentration problem where no-slip goes over into viscous sliding becomes mathematically amenable to analysis, at least approximately. This situation corresponds to a glacier which is cold in the lower and temperate in the upper parts. Our situation corresponds to that discussed by Reference MullerMüller (1976). The reverse also occurs, and is believed to arise more frequently; it can be obtained from our analysis by simply selecting the angle γ as negative (this angle is described in section 2 and Figure 1). The abrupt change in boundary condition from no-slip to viscous sliding will induce large stress and velocity variations. The maximal stresses are to be expected at the “discontinuity” of boundary data.

Fig. 1. Flow of ice down a strictly parallel sided slab can be modelled approximately by treating a channel-flow problem of ice held between two plates which are twice as far apart as the ice strip is deep. Inclination of the slope is γ and the basal boundary conditions are no-slip (u = v = 0) and viscous sliding, respectively.
One question of geomorphological interest is whether these stresses are sufficiently high to tear off portions of the rock base. If they are, a partial explanation of the substantial amount of till observed at the bottom of an ice bore hole (Reference Engelhardt, Harrison and KambEngelhard and others 1978) could be explained. This, then, is the question to which we shall address ourselves, and indeed we shall demonstrate that the removal of rock from the base in the above-mentioned conditions is possible.
2) Mathematical Problem
An infinite, parallel-sided ice slab under plane motion is studied, the upper half of the base of which adheres to the bed while the lower half of the bed is subject to viscous sliding. Of interest is the stress distribution induced by gravity and, in particular, its behaviour near the abrupt change of boundary data. The exact problem based on non-linear rheology (e.g. Glen's flow law) is hardly amenable to an analytical solution, but by restricting attention to Newtonian behaviour approximate solutions can be obtained with reasonable effort. Although the Newtonian model suffers the disadvantage of not being materially realistic for ice, it is a useful one because it allows the solution of a well-defined mathematical problem free of ad hoc assumptions. The same applies to the many other linear models introduced into the ice literature (Reference NyeNye 1969 and Reference Nye1970, Reference KambKamb 1970, Reference LliboutryLliboutry 1975, Reference MorlandMorland 1976[a] and Reference Morland1976 [b], Reference MorrisMorris 1979, Reference Hutter and OlunloyoHutter and Olunloyo 1980).
Specifically, consider slow flow of a Newtonian viscous fluid held between two parallel planes whose inclination angle is γ and which are at a distance 2D apart (Fig. 1). Let (x, y) be a Cartesian coordinate system; x is midway between the two planes and y perpendicular to it, so that the two planes confine the fluid to the region |y| ≤ D. We assume mixed boundary conditions, namely no-slip for x>0 and viscous sliding for x≤0. The sliding law will be taken in the form of Equation (l) with m=1 and a coefficient C(x) that varies with x. This x-dependence will be further elaborated below. Let ρ be the density, g the gravity constant, μ the dynamic viscosity, (u, v) the longitudinal and transversal velocity components, and p the pressure. The governing equations describing steady flow through the above channel are given by the differential equations (Fig. 1):

subject to boundary conditions:

Equations (2) express mass balance for an incompressible body and momentum balance when convective acceleration terms are neglected. The first of Equations (3), on the other hand, expresses the no-s1ip boundary condition, where as the second of (3) is the viscous sliding law. Because of its physical significance the latter warrants further attention.
We assume the sliding coefficient to vary along the temperate part of the boundary, typically as shown in Figure 2. At large values

Fig. 2. A typical assumed variation of the viscosity coefficient in the basal sliding law. At the transition point where temperate ice becomes cold C=C 0 is minimal and may even have the value C 0= 0.This would then correspond to a continuous transition from no-slip to viscous sliding.
of |x|, effectively for |x|> δ, where δ is a transition length, the sliding coefficient is nearly constant with a value approaching C ∞ as |x|→∞. For 0 ≤|x|≤ δ, C depends on x, starting at x = 0- with a value C 0 and then monotonically increasing, approaching the value C ∞ effectively at x = -δ. We regard this variation as a reasonable model for the description of the transition from viscous sliding to no-slip. Close to x = 0 a decrease of C with decreasing |x| is most likely to occur since the number of cold patches will increase as the cold portion of the base is approached. We assume that the transition depth δ must be small compared with the glacier thickness D; it is, however, physically not clear whether C 0 differs from zero or must vanish. Reference FowlerFowler's work (1979 [a])suggests that C 0 should vanish, and he claims that in this case both stresses and velocities remain bounded at the point of discontinuity of boundary data. Reference Hutter and OlunloyoHutter and Olunloyo (1980), on the other hand, have shown that for C 0 = C ∞ → ∞ (corresponding to perfect slip), the stresses show half-order singularities at the point x = 0. It is thus expected that the details of the stress and velocity distributions will depend on the transition properties of the sliding law in the neighbourhood of the transition point “temperate-cold”. As a consequence, the failure criterion for the rock beneath will also depend on the pertinent details of the sliding law.
Mathematically, the boundary value problem set forth by Equations (2) and (3) can be shown to be reducible to a problem of the Wiener-Hopf type (Reference Hutter and OlunloyoHutter and Olunloyo 1980), and it is in the form of the latter that an approximate solution can be found. Symmetry of the mathematical formulation about y = 0 is obtained by having identical boundary conditions on y = ± D, by redefining pressure to incorporate transverse components of the gravity forces, and by imposing zero transverse velocity andˊ zero shear traction, but not zero normal traction, on the surface y = 0. This is not entirely realistic as shear and normal tractions should vanish on the true free surface, but, for perfect slip on the temperate side, calculations indicate that p on y = 0 is small and does not affect the singularity. The details of the construction of the solution of the Wiener-Hopf problem are very elaborate (as shown by Olunloyo and Hutter, unpublished). In the following section the most important results pertinent to the problem at hand will be discussed.
3) Basal Stresses Near The Point Of Abrupt Changes Of Boundary Data
A possible mathematical representation for the dimensionless viscosity coefficient in the sliding law as depicted in Figure 2 is

In this equation the various forms of C are made dimensionless with D/(2μ) so that C dim = CD/(2μ) Similarly, x̅ and δ are dimensionless lengths based on D, the glacier thickness. With C dim = u b/τ b and with u b = 100 m a-1, τb = 105 Pa, D = 102 m and μ=105 Pa, a reasonable value for C is about 2.
The Wiener-Hopf problem based on Equations (2), (3) and (4) was solved by approximating the kernel of the Wiener-Hopf equation. Two approximations have been found. The first is valid, provided that C 0= C ∞ →∞ and when the boundary condition at the temperate side is that of perfect slip (Reference Hutter and OlunloyoHutter and Olunloyo 1980). The other applies for viscous sliding according to the functional representation of Equation (4) and holds for any finite value of C ∞ and any va1ue of C 0 /.C ∞ in the interval [0, l].
Let Σ x , Σ y , Θ be dimensionless normal and shear stresses at the base, respectively, which have no dimensions with respect to the basal shear stress ρgD sin γ of the strictly parallel-sided slab. Hence, orders of magnitudes to be expected for Σ x , Σ y and Θ in a strictly parallel-sided slab are 10 and 1, respectively. For the special case that C 0 = C ∞→∞ the functions Σ x(x) , Σ y(y) and Θ(x) have been evaluated. For the more general relationship of Equation (4) explicit formulas for the basal stresses are probably difficult to find, but asymptotic re-presentations for small |x| can be found with reasonable effort. The expressions have the general form

in which ƒ stands for either shear stress, overburden, or longitudinal stress Θ , Σ x , and Σ y. Notice that υ may have the value -1, so that the stresses may have a square-root singularity. Indeed, calculations show that the shear stress is regular as x = 0- is approached from the temperate side, but becomes singular when x = 0+ is approached from the cold side. The singularity is of square-root type and can be integrated. When integrated to lowest order one obtains

with coefficients which are functions of C
0 , C
∞ and δ. Detailed analysis shows that ![]() is finite and differs from zero for all values of C
0/C
∞ in the interval [0, 1]. Consequently the square-root singularity persists even in case the coefficient function C(x) is continuous at x =0.
is finite and differs from zero for all values of C
0/C
∞ in the interval [0, 1]. Consequently the square-root singularity persists even in case the coefficient function C(x) is continuous at x =0.
Explicit calculations are too elaborate for arbitrary values of the transition length δ, but become much simplified when δ = π-1. This value corresponds to a transition length which is about one-third of the glacier thickness. This should be borne in mind. The basal shear stress reads

where β is a function of C 0 and C ∞ and can be read off from Table I. This table shows the product C ∞β as a function of (C 0- C ∞); see also Figure 3. It should also be noticed that in the limit C 0 = C ∞→∞ Equation (7) breaks down and results must be obtained from the earlier investigation (Reference Hutter and OlunloyoHutter and Olunloyo 1980).
Table I. Coefficient β as a function of the parameter (1-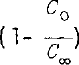 ) and residue indicating the accuracy of the root
) and residue indicating the accuracy of the root


Fig. 3. Functional dependence of the coefficient S as a function of (1-![]() ).
).
For the longitudinal normal stress and the overburden pressure, the singular behaviour is more sensitive to variations in boundary data than is the case for the shear tractions. When the perfect slip condition is applied at the temperate side, both stress components Σ x and Σ y are singular at x = 0 with square-root singularities. On the other hand, when the viscous sliding law (1) is used, the singularity in the longitudinal stress Σ x persists while overburden pressure is now finite. This is an indication that with a decrease in singularity in boundary data smoother stress fields should be obtained. To be sure, asymptotic representations for Σ x and Σ y are

and

With

where D -3(.) is the parabolic cylinder function. Of particular interest is the coefficient of the x -1/2 term in Equations (7) and (8) because it determines the dominant parts of the stresses Θ and Σ x . Values for this coefficient are plotted as shown in Figure 4. This graph is for the coefficient of Σ x which is twice as large as the corresponding coefficient for Θ. The singular behaviour expressed by square-root singularities occurring in Equations (7) and (8) points at a possibility of failure or removal of basal rock; in fact, square-root singularities are also expected in the principal stresses at the base so that from a theoretical point of view both ice

Fig. 4. Plot of the coefficient of the singular term in the stress expansion as given in the Equations (7) and (8).
and rock must fail if a failure criterion under tensile stress is assumed. Asymptotic expressions for the principal stresses Σ1 and Σ2 can be obtained by using the formula

and upon substitution of the expansions. The dominant term is

It is interesting to observe that the principal stresses are singular on both sides of the discontinuity of boundary data. In contrast to the stresses, forces remain finite, however, because it is possible to integrate the singularities. Therefore integrating the stresses over a small length ε yields (in physical dimensions):
as a typical value for the tensile force acting perpendicularly to a possible failure plane. This tensile force arises for both positive and negative slope γ but acts on planes of different orientations in these instances.
A typical value for ![]() , is about 1 or 2 so that with ρ=9x102 kg m-3, g=9.8 m S-2, sin γ = 10-2, D=102 m and ε=10-1 m, F
1=2x103 N. Hence the average maximal tensile stress acting on an element of 10-2 m2 area in a possible failure plane is about σ
1 = 2x105 Pa. This is in the order of the failure strength of ice under uniaxial tension and is probably also sufficiently high for rocks, provided they contain a sufficient amount of microcracks. Of course, on a smaller scale. mean stresses are larger.
, is about 1 or 2 so that with ρ=9x102 kg m-3, g=9.8 m S-2, sin γ = 10-2, D=102 m and ε=10-1 m, F
1=2x103 N. Hence the average maximal tensile stress acting on an element of 10-2 m2 area in a possible failure plane is about σ
1 = 2x105 Pa. This is in the order of the failure strength of ice under uniaxial tension and is probably also sufficiently high for rocks, provided they contain a sufficient amount of microcracks. Of course, on a smaller scale. mean stresses are larger.
4. Some Final Remarks
The purpose of the above linear analysis is twofold: first, it can be used to substantiate the supposition that stress concentrations at the melting point of the base in a polythermal glacier are sufficiently high to tear off from the base rock pieces as seen in field observations; second, the analysis gives information about the nature of this stress concentration, as it depends on the variation of the sliding coefficient C. We reported that for the sliding law obeying Equation (4) stress singularities persist even when c(x) is continuous (but not differentiable) at x = 0. This does not imply that stresses which are large but bounded at x = 0 cannot exist, but that bounded stress would require a smoother transition of the sliding coefficient from cold to temperate sides. Morland (private communication) suggests such a smoother transition by requiring a viscous sliding condition to be valid everywhere at the boundary, whereby the sliding coefficient C would. approach infinity as the temperate side is approached. We have not analysed this case, and the problem is a global one, “local” stresses in the basal layer are likely to be concentrated, and induce bed failure. This points clearly at the difficulty associated with the sliding condition. Nothing is known at present about the sliding law close to the cold-temperate transition zone and the associated stress concentrations.
Removal of rock from the base can also be explained by mechanisms other than stress concentrations due to abrupt changes in boundary data only. Reference Rӧthlisberger and IkenRothlisberger and Iken (1981) give such an alternative based on a regelation argument when basal cavities are formed. Their model explains how pieces of basal rock, that have already broken loose, are transported by the ice; our model suggests why the basal rock fractures into pieces.
Finally it should be mentioned that our calculations can only be regarded as approximations because effects of regelation and nonlinearities of the creep behaviour have been omitted. It is unlikely that these effects can be included in a quantitative analysis. Yet we think that our model gives orders of magnitude correctly.







