Introduction
Avalanche forecasting involves the assimilation and prediction of data and information describing weather, snowpack and stability within a given time period and spatial extent, and assimilating this information to assess the likelihood of avalanches in the future. In conventional avalanche forecasting, this process is carried out with little or no direct use of numerical models by avalanche forecasters, who tend to apply a range of diverse and redundant data sources to the problem (Reference LaChapelleLaChapelle, 1980). Avalanche forecasts may be provided for periods in the future ranging from the next few hours (e.g. in the management of avalanche hazard for roads) through to the next day (commonly the case in the provision of avalanche forecasts for recreationalists) to forecasts covering periods of several days in areas with relatively low temporal variability in weather conditions. Similarly, spatial forecast scales can vary from a specific (at the level of a single avalanche path), through local forecasts for a particular region (e.g. a ski area) to regional forecasts for a significant part of a mountain range (Reference McClung and SchaererMcClung and Schaerer, 1993).
Over the last two decades, a wide range of numerical models and tools have been developed to assist avalanche forecasters in the decision-making process, ranging from physical models of the development of the snowpack (Reference Bartelt and LehningBartelt and Lehning, 2002), through expert systems, which attempt to integrate expert knowledge (Reference Schweizer and FöhnSchweizer and Föhn, 1996), to a variety of statistically based methods. In general, the most commonly used approaches in operational avalanche forecasting are based around statistically based methods, although physical models and expert systems have been and are being incorporated in forecasting.
The family of statistically based techniques used in avalanche forecasting includes discriminant analysis, regression trees and nearest neighbours (NN) (Reference Obled and GoodObled and Good, 1980; Reference BuserBuser, 1983; Reference Davis, Elder, Howlett and BouzaglouDavis and others 1999). Of these, by far the most widely used in operational forecasting appears to be NN. The core of NN methods lies in the assumption that similar events are likely to occur under similar conditions. In avalanche forecasting, the data describing the likelihood of avalanches are often divided into three classes, Class III meteorological factors, Class II snowpack factors and Class I stability factors, where higher class numbers are considered to be less directly related to avalanching (Reference McClung and SchaererMcClung and Schaerer, 1993). Thus, in principle, an approach to avalanche forecasting based on stability factors should have better forecasting skill than one based on meteorological factors. In practice, data describing meteorological and snowpack factors are generally easier to collect and generalize over a larger region and are more commonly used in avalanche forecasting at the local and regional levels. NN approaches tend to use mostly Class III and some Class II data (e.g. Reference BuserBuser, 1983; Reference Brabec and MeisterBrabec and Meister, 2001; Reference McCollister, Birkeland, Hansen, Aspinall and ComeyMcCollister and others, 2003; Reference Purves, Morrison, Moss and WrightPurves and others, 2003) to describe the similarity of conditions leading to avalanches. Given a set of forecast data, a sorted list of previous days together with the events that occurred on these days is returned to the forecaster. The sorted list is created by using a distance metric (usually Euclidean) to compare scaled and weighted data with the forecast data. Reference Heierli, Purves, Felber and KowalskiHeierli and others (2004) argued that three possible interpretations of NN existed:
-
categorical forecasts, where some decision boundary is used to classify forecast days as avalanche days or not;
-
probability forecasts, where the proportion of the number of nearest neighbours with avalanche days is interpreted as the probability of an avalanche on the forecast day; and
-
descriptive forecasts, where experts interpret and incorporate a detailed list of events into their decision-making process.
NN appears to be relatively popular with forecasters because of the possibility of the latter interpretation, which accords well with conventional inductive avalanche-forecasting processes (Reference LaChapelleLaChapelle, 1980). However, NN is a relatively simple pattern-classification technique and it has been argued that such methods are very prone to over-fitting in highly dimensional data (Reference McCollister, Birkeland, Hansen, Aspinall and ComeyMcCollister and others, 2003). In recent years, a family of theoretically grounded techniques based on statistical learning theory (SLT), a general mathematical framework for extracting dependencies from empirical data, has emerged (Reference VapnikVapnik, 1995).
The general approach to statistical learning from data is based on minimizing the error of the model on the training data, whilst simultaneously maintaining low complexity. Such approaches have been shown to avoid over-fitting and to provide promising predictive abilities in a range of problems based around highly dimensional data such as text, images, and gene data of bioinformatics (Reference Guyon, Weston, Barnhill and VapnikGuyon and others, 2002).
In this paper, we explore the use of support vector machines (SVMs), a machine learning approach derived from SLT. SVMs aim to be independent of the dimensionality of the input space and are designed to deal with non-linear problems in a robust and non-parametric way. First, we briefly introduce the background of SVM techniques, before presenting a case study of their application to avalanche forecasting in Scotland, UK. We then illustrate the ability of SVMs to produce categorical and probabilistic forecasts, before showing an example of the possible extension of SVM to the production of spatially variable forecasts within a forecasting region and discussing the potential of using SVMs in operational avalanche forecasting.
Support Vector Machines
The initial assumption underlying SVMs is that given a set {(x 1,e 1),(x 2,e 2), . . . , (xn ,en )}, where xi is an m-dimensional vector describing the conditions at a given time and ei is a binary event associated with this vector, a hyper-plane which cleanly separates the binary events can be identified (Fig. 1a). It has been shown in SLT (Reference VapnikVapnik, 1995) that the hyper-plane that provides the maximum margin between classes will provide the best generalization and lowest validation error (Fig. 1b). Only a small subset of the vectors x i , which lies at or near the decision boundary, is required to identify this hyper-plane. The vectors are known as the support vectors. The hyper-plane is constructed with regard to the fact that in most real-world datasets data are noisy and some vectors can be mislabelled.

Fig. 1. Schematic illustration of SVM. The validation data are not used in identifying the decision boundary.
The next extension of SVMs consists of indirectly mapping the input space into a higher-dimensional space using kernel functions (Reference Schölkopf and SmolaSchölkopf and Smola, 2001) and finding an optimal separating hyper-plane through quadratic programming. This leads to a non-linear decision function f (x) in the initial feature space, which takes the form of a kernel expansion, i.e. for any vector of input features x,
where xi is a feature vector describing conditions at a given time, ei is the binary event described by xi , αi is a weight constrained such that 0 ≤ αi ≤ C, and K(x,xi ) is a kernel function.
The kernel function must be symmetric and positive definite, and is usually a Gaussian radial basis function with some radius σ. Thus, the algorithm has two parameters, C, describing the possible range of weights, and σ, the radius of the kernel function. In real-life problems, where the data are noisy or do not completely describe the events, increasing the value of C increases the range of possible weights and allows more vectors to contribute to the function, thereby also increasing the danger of over-fitting. Thus, C can be considered to be some measure of data quality with respect to the events. The value of σ describes the radius of the smoothing function, with higher values resulting in a more generalized form of the decision function.
These two parameters, σ and C, must be tuned to minimize misclassification by using cross-validation on either a training-data or a testing-data subset. The function f(x) can be interpreted in terms of a categorical decision for some value of forecast vector x according to some default threshold value of f(x). However, it is also possible to probabilistically interpret the outputs by post-processing, for example through taking a sigmoid transformation of f(x) (Reference Platt, Smola, Bartlett, Schölkopf and SchuumansPlatt, 1999). The resulting transformation gives
where A and B are constants.
Generally, A and B are tuned using a maximum-likelihood estimator using bootstrapping on the training data. If B is found to be close to zero, then the default threshold coincides with a probability of 0.5.
Implementing a SVM For Avalanche Forecasting
In this paper, we report on the implementation of a SVM for a dataset used in an NN-based avalanche-forecasting tool in Scotland. Scotland has a maritime climate characterized by high wind speeds and rapid temperature changes, and lies at a relatively northerly latitude (~578 N) with mountains of, by Alpine standards, low elevations (<1300 m). The data used were collected in the Lochaber region, one of five areas in Scotland where avalanche forecasts are produced. The region includes Scotland’s highest mountain Ben Nevis and some of Scotland’s most popular winter climbing venues. New snow is accompanied by high winds and intense snowdrifting, with the 0˚C isotherm moving above and below summits many times in the average winter. During the winter avalanche season, forecasters are in the field on a daily basis, and the data used in the SVM are a mixture of those collected by the forecasters and downloaded from an automatic weather station.
Data preparation and feature selection
The original data consist of daily measurements of ten meteorological and snowpack variables. Combining these data with data for two previous days, an input feature vector with 30 dimensions was created. Most of these measurements are relatively standard, but because of the large amount of redistribution of snow by wind and the corresponding difficulties in measuring new-snow depths, the forecasters measure new snow on an ordinal scale, which can be summed to give cumulative totals. Because, by contrast to NN, SVMs are designed to deal with highly dimensional data, the feature vector was further extended in a dialogue with an avalanche forecaster for the Lochaber region, who was asked to list important indicators of avalanche activity. These expert features included a cumulative snow index (describing the sum of a snowfall index), change in air temperature over the previous 2 days, snow temperature gradients, and a number of binary indicator variables including air temperature crossing 0˚C, avalanche activity on two previous days, strong southeasterly winds on previous days, snowdrifting, and poor visibility during the previous 2 days. The final feature vector included a total of 44 variables.
An initial step in identifying suitable features used recursive feature elimination in conjunction with a SVM to filter redundant features (Reference Guyon, Weston, Barnhill and VapnikGuyon and others, 2002). This feature selection method iteratively omits the variables with the smallest influence on the decision surface of the SVM classifier. The list of 20 features, which were found to be the most valuable for SVM classification, is given in Table 1. It is important to stress that these features were selected in a purely data-driven way.
Table 1. The list of features selected by recursive feature elimination algorithm, grouped by type: features related to the current or previous days and expert variables

One important characteristic of the selected features appears to be the retention of almost all Class II (snowpack) information, including the unfortunately rather noisy and subjective foot-penetration values. Current air temperature is not retained, but this information is available to the system through the previous day’s air temperature and air-temperature gradient. Half of the expert features are retained, with south or southeasterly winds perhaps particularly important, since the main climbing venues are found on north-facing slopes. Furthermore, given the rapid nature of change in Scotland’s maritime climate, it is notable that only two non-expert features (foot penetration and wind direction) are retained 2 days before the forecast day.
Training
The data were divided into a training set of 1123 samples (winters 1991–2000) and a validation set of 712 samples (winters 2001–07). The validation dataset was only used to assess the results and was not available during the training phase. To select values for the parameters σ and C, training and cross-validation surfaces were generated using a wide range of values of σ and C. Figure 2 shows the training error surface (the error of the model predicting the training data), with the minimum classification error lying at the top left of the figure (i.e. for the maximum value of C and minimum value of σ). However, as shown by the cross-validation error surface, choosing these values of σ and C would result in over-fitting. The cross-validation error surface is generated by systematically removing one feature vector from the dataset and calculating the error of its prediction by the model. Values of σ and C were selected to lie roughly in the centre of the central band with low errors, with σ = 12 and C = 25, thus minimizing cross-validation error whilst having an acceptable training error.

Fig. 2. SVM training error surface (left) and cross-validation error surface (right). The classification error is a percentage of correctly classified data samples: (Hits + Correct Negative)/(Total Number of Samples).
Validation
As discussed above, the results of NN forecasts can be interpreted categorically, probabilistically or descriptively. Here we present the results of a categorical and probabilistic validation of the implementation of the SVM on the independent validation dataset of 712 samples (2001–07). We follow the methodology of Reference Heierli, Purves, Felber and KowalskiHeierli and others (2004) by first investigating the influence of different threshold values on a range of forecast-verification measures (Table 2).
Table 2. Forecast-verification measures (Reference Doswell, Davies and KellerDoswell and others, 1990; Reference WilksWilks, 1995)

The sensitivity of these measures to threshold values of SVM between 0 and 1 is shown in Figure 3. In choosing a threshold for categorical forecasts, a decision must be made about the acceptance of different forms of forecast error. For example, low threshold values maximize the probability of detection (i.e. the chances of missing an avalanche event are minimized), whilst leading to increased false alarms. Figure 3a shows that a reasonable compromise between probability of detection (PoD) and hit rate lies somewhere between values of around 0.4 and 0.6. In Figure 3b, skill scores that describe the ability of a technique to forecast better than by random chance are shown. Here, the Heidke skill score once again suggests an ideal threshold value lying between about 0.4 and 0.6, whilst the Kuipers skill score suggests slightly lower threshold values.

Fig. 3. (a) Forecast-accuracy and (b) forecast-skill measures. The x axis corresponds to the SVM threshold.
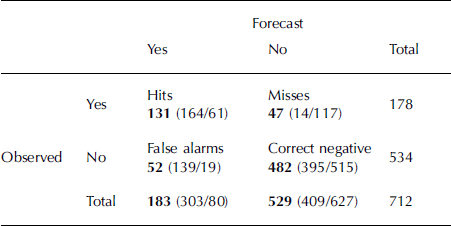
Table 3 shows the joint distribution of forecasts and observations for binary categorical forecasts for the selected threshold value and two other threshold values, and allows the calculation of any forecast-accuracy or -skill measure. When a low threshold (0.25) is selected, more avalanches are correctly forecast (164), at the cost of many more false alarms (139). Equally, when a higher threshold (0.75) is used, many more misses occur (117), though the number of correct negatives also increases (515). These results confirm that a sensible threshold value lies, for these data, around a value of 0.5.
Table 3. Joint distribution of forecasts and observations for binary categorical forecasts and the obtained values for default SVM threshold of 0.5 (values in parentheses are for thresholds of (0.25/ 0.75) respectively)
As explained above, it is also possible to probabilistically interpret the output of SVMs. To evaluate the quality of this output, we calculated the empirical probability of an event for a given range of values. Figure 4 shows the resulting curve. It can be seen that the forecast probabilities generally agree well with the empirical probability of events, especially for cases with higher probabilities. At lower probabilities, the results show less resolution, suggesting that the values of the parameters of the transformation (Equation (2)) may not be ideal.

Fig. 4. The verification of probabilistic output of the SVM with reliability diagram (Reference WilksWilks, 1995). The x axis indicates the probability value of the decision threshold, and the y axis the empirical probability of the observed avalanches in the days corresponding to the selected threshold. Points close to the black line have the best skill; those closer to the horizontal line have no resolution.
Figure 5 shows SVM predictions for a single winter in the validation dataset and the corresponding avalanche events. It can be seen that, qualitatively, there is good agreement between events and periods assigned high probabilities for this time period.

Fig. 5. The prediction of SVM for the validation data of winter 2003/04. The observed events are plotted as black boxes (or continuous series of black boxes) at 0 (no events) and 1 (avalanche activity) levels. The probabilistic output of SVM is plotted as a continuous curve. The x axis corresponds to time in days.
Extending the SVM to Spatial Avalanche Predictions
Since SVMs are well suited to high dimensionality it is relatively straightforward to add some level of spatial forecasting to an SVM. In the case of Lochaber, information about some 700 avalanche events for 49 individual avalanche paths was available. Thus, for every day in the dataset, a feature describing the meteorological and snowpack parameters, the altitude, aspect (presented as north/south and east/west components) and gradient of each path was added. This results in a much larger number of feature vectors with the same total number of avalanche events. Meteorological and snowpack data were treated as constants over the region. The SVM can then be used to generate a spatial avalanche forecast, extrapolated over the region through the use of a digital elevation model (DEM), based on the enhanced feature vectors. Figure 6 shows the results of such a forecast, which appears to agree well with the location of observed avalanches for the day. However, it is important to emphasize that these are early results intended to illustrate that SVMs can be used in spatial avalanche forecasting, and more work is needed to consider the validity of the results.

Fig. 6. (a) DEM of the Lochaber region. The locations of avalanche paths are shown with circles. (b) The sample output of the spatio-temporal SVM model, indicating the probability of the event on 20 January 1991. The actual observed events are shown with circles.
Discussion
A key motivation for this paper lies in the desire to apply one member of a family of techniques derived from SLT to avalanche forecasting. We have demonstrated that SVMs produce categorical results in avalanche forecasting which are comparable with a baseline technique (NN) operationally used in the region (Reference Purves, Morrison, Moss and WrightPurves and others, 2003). The NN approach was applied to the dataset (without the expert features) considered in this paper, giving performance values broadly comparable with those shown by SVMs at optimum thresholds of 0.5 in Figure 3. However, the number of neighbours that have to be used to provide the best performance was found to be relatively high (around 20) (Fig. 7).

Fig. 7. Training error and cross-validation error curves used to identify the optimal number of neighbours.
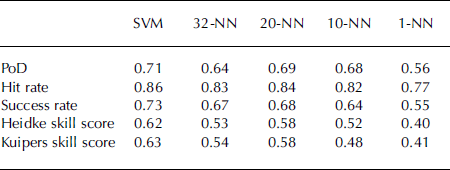
Results obtained from NN on the validation data (winters 2001–07) are summarized in Table 4. Interestingly, the best prediction with the NN model was observed using 20 nearest neighbours, while the use of 10 or a single nearest neighbour produces a drop in performance. This is likely to be due to the ‘curse of dimensionality’ whereby, as the number of features is increased, the NN method requires more neighbours. Note that while a 20-NN model was found to provide good results, the descriptive interpretation of a forecast based on 20 events becomes complicated.
Table 4. Performance measures for the SVM and NN models computed on the validation dataset of 712 days (winters 2001–07)
Concerning the descriptive interpretation of SVM forecasts, the features identified by the recursive feature removal are in accordance with what might be expected for this region, with the Class II (snowpack) features being preferentially retained and a number of, apparently redundant, meteorological features being removed. It is important to note here that feature selection and extraction opens promising perspectives for improving the current SVM model. Since a key ingredient in the acceptance of avalanche-forecasting tools is the transparency and interpretability of the input data, and because SVM are not black boxes, it is possible not only to identify which features contribute to the classification of avalanche and non-avalanche events, but also to examine the individual support vectors. Since SVMs aim to identify a small number of support vectors, which contribute to the definition of the hyper-plane, there is potential to explore which support vectors lie at or near the decision boundary and consider the physical meaningfulness of the features of these vectors.
Figures 4 and 5 illustrate the probabilistic interpretation of the output from the SVM. Once again, SVM techniques appear to show reasonable performance in producing probabilistic outputs.
However, the performance of SVMs in terms of both categorical and probabilistic measures is not significantly better than equivalent NN techniques, such as those reported for the Lochaber region by Reference Heierli, Purves, Felber and KowalskiHeierli and others (2004). Rather, it is in the potential wider application of SVMs to avalanche forecasting that we see considerable potential. Since SVMs are specifically designed to take high-dimensional data and extract a sparse set of support vectors from such data, they are applicable to problems with very low base rates, such as the forecasting of avalanches for individual avalanche paths. This is in contrast to NN, where the high dimensionality of the problem makes the application of a technique based on Euclidean distances, where all features are considered in every forecast, unlikely to be successful. This ability to deal with high dimensionality also makes SVMs flexible: it is possible to add different types of information to the feature vector; for example, in this paper we illustrate how spatial data might be added to the feature vector. Importantly, since the original data are not transformed it is also possible to apply the resulting probability function to generalize the solution over space. This part of our work is in its early stages, and considerable further research will be required to investigate the validity, as opposed to the feasibility, of applying SVMs to spatial avalanche forecasting. Further work is also necessary in investigating the uncertainties associated with the results of SVMs.
Conclusions
In this paper, we have illustrated the application of a SVM to avalanche forecasting for a dataset from Lochaber. Initial results show that the SVM’s forecasting performance for categorical and probabilistic forecasts is comparable to baseline NN methods on an independent validation dataset. Since the features used are untransformed, the method could also be used to produce descriptive forecasts and is likely to be suitable for operational avalanche forecasting.
SVMs have a number of promising aspects, which will be the focus of further work:
-
A small number of support vectors contribute to the result; exploration of these may provide insight into avalanche forecasting.
-
SVMs are well suited to solving problems with very high dimensionality, in contrast to NN. Thus, feature vectors containing a wide range of features from a variety of sources can be created. Such features might include more snowpack data extracted from physical models such as snowpack (Reference Bartelt and LehningBartelt and Lehning, 2002). The lack of features representing snowpack data, and the implications of increasing dimensionality, is a weakness of NN approaches.
-
This applicability to problems of high dimensionality allows the extension of SVMs to the production of spatially distributed avalanche forecasts. Future work will investigate whether such approaches can produce useful results.
Acknowledgements
The research was supported by Swiss National Science Foundation projects ‘GeoKernels: Kernel-Based Methods for Geo- and Environmental Sciences’ (project No. 200021113944). G. Moss and the sportscotland Avalanche Information Service are thanked for their assistance in identifying expert features and the provision of data for Lochaber.







