Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-22T14:59:17.907Z Has data issue: false hasContentIssue false
  • English
  • Français

An empirical relation between overburden pressure and firn density

Published online by Cambridge University Press:  20 January 2017

Takao Kameda Hitoshi Shoji ,
Kunio Kawada ,
Okitsugu Watanabe  and
Henrik B. Clausen
Takao Kameda Hitoshi Shoji
Affiliation:
Kitami Institute of Technology, Koencho 165, Kitami, Hokkaido 090, Japan
Kunio Kawada
Affiliation:
Department of Earth Sciences, Toyama University, Gofuku 3190, Toyama 930, Japan
Okitsugu Watanabe
Affiliation:
National Institute of Polar Research, Itabashi, Tokyo 173, Japan
Henrik B. Clausen
Affiliation:
Department of Geophysics, The Niels Bohr Institute, University of Copenhagen, DK-2200 Copenhagen .N, Denmark
Rights & Permissions [Opens in a new window]

Abstract

Two empirical equations for firn densification have been obtained,considering firn porosity as a function of overburden pressure. In the first equation, thereduction ratio of porosity in firn is assumed to be proportional to the increasing ratioof overburden pressure and the mth power of the porosity. The porosity exponent m should be close to -2, so as to have a best-fit with 14 depth-density profiles fromGreenland and Antarctica. In the second equation, the reduction ratio of porosity wasassumed to increase proportionally to the increment of overburden pressure and thenth power of the porosity. The most satisfactory values of the exponent range from -1 to 1. It has been suggested that firn density, determined primarily by overburdenpressure and firn temperature, contribute to a lesser degree.

Type
Research Article
Information
Annals of Glaciology , Volume 20 , 1994 , pp. 87 - 94
Copyright
Copyright © International Glaciological Society 1994

1 Introduction

The transformation process of firn to ice is one of the most fundamental subjects in polar ice-sheet studies. A number of theories regarding the dry densification of firn have been proposed (Reference RobinRobin, 1958 Reference SchyttSchytt, 1958 Reference BaderBader, 1960, 1962 Reference Benson Benson, 1962 Anderson and Reference BensonBenson, 1963 Reference KojimaKojima, 1964 Reference GowGow, 1975). However, a comprehensive model including grain-settling, sublimation/condensation, volume/ surface diffusion, ice deformation and recrystallization processes has not been firmly established. The densification processes have also been studied empirically (Reference RobinRobin, 1958 Reference SchyttSchytt, 1958 Reference Herron and LangwayHerron and Langway, 1980 Reference LingLing, 1985 Reference Langway, Shoji, Mitani and ClausenLangway and others, 1993). Reference SchyttSchytt (1958) found an empirical relation between firn density and the weight of overlying snow. Reference Herron and LangwayHerron and Langway (1980) investigated the validity of Schytt,s equation using 17 depth-density profiles from Greenland and Antarctica. Reference Langway, Shoji, Mitani and ClausenLangway and others (1993) showed a simple relation between overburden pressure and firn density

This paper focuses on obtaining a simple equation fora relationship between overburden pressure and firndensity from the surface to the depth of pore close-off considering the studies by Reference SchyttSchytt (1958) and Langwayand others (1993).

2 Analytical Procedure

Instead of using the snow densification law (Reference BaderBader, 1960,1962), an assumption was made that snow behaves like aperfectly plastic material. That is, porosity, s(= (ρi - ρ)/ ρi) is determined only by overburden pressure, P, at each depth level. ρis the firn density and ρi is the bubble-free ice density at -20°C (0.919.Mgm-3). When the pressure P increases to P +dP, s decreases to s-ds. Thereduction ratio of porosity, -ds/s was assumed toincrease proportionally to the increasing ratio of pressure, dP/P and the mth of power of s as follows:

(1)

where C and mare constants.

We obtained the following equations by integrating Equation (1):

(2)
(3)

where C1, C2, C3and C4 are constants.

Another equation was obtained by assuming that the reduction ratio of porosity, -ds/s increases proportionallytothe increment of pressure, dP, and the nth power of s as follows:

(4)

where D and n are constants.

Thus, we obtained the following equations:

(5)
(6)

where D1, D2, D3and D4are constants.

Recently, Reference Langway, Shoji, Mitani and ClausenLangway and others (1993) showed a linearrelation between (ρi-ρ)2and In(P) from the surface to.the depth of pare close-off for three sites in Greenland andAntarctica. If we rewrite the expression(ρi-ρ)2of Langway and others (1993) to ((ρi-ρ)/ρi)2, the relation is expressed as follows:

(7)

where E1 and E2are constants.

This equation is identical with Equation (2) with m=-2.

On the other hand, Reference SchyttSchytt (1958) proposed the following relation between firn density (ρ) and depth from the surface (h) far the Maudheim Ice core,Antarctica:

(8)

This equation is identical with Equation (4) with n = 0.

3 Results

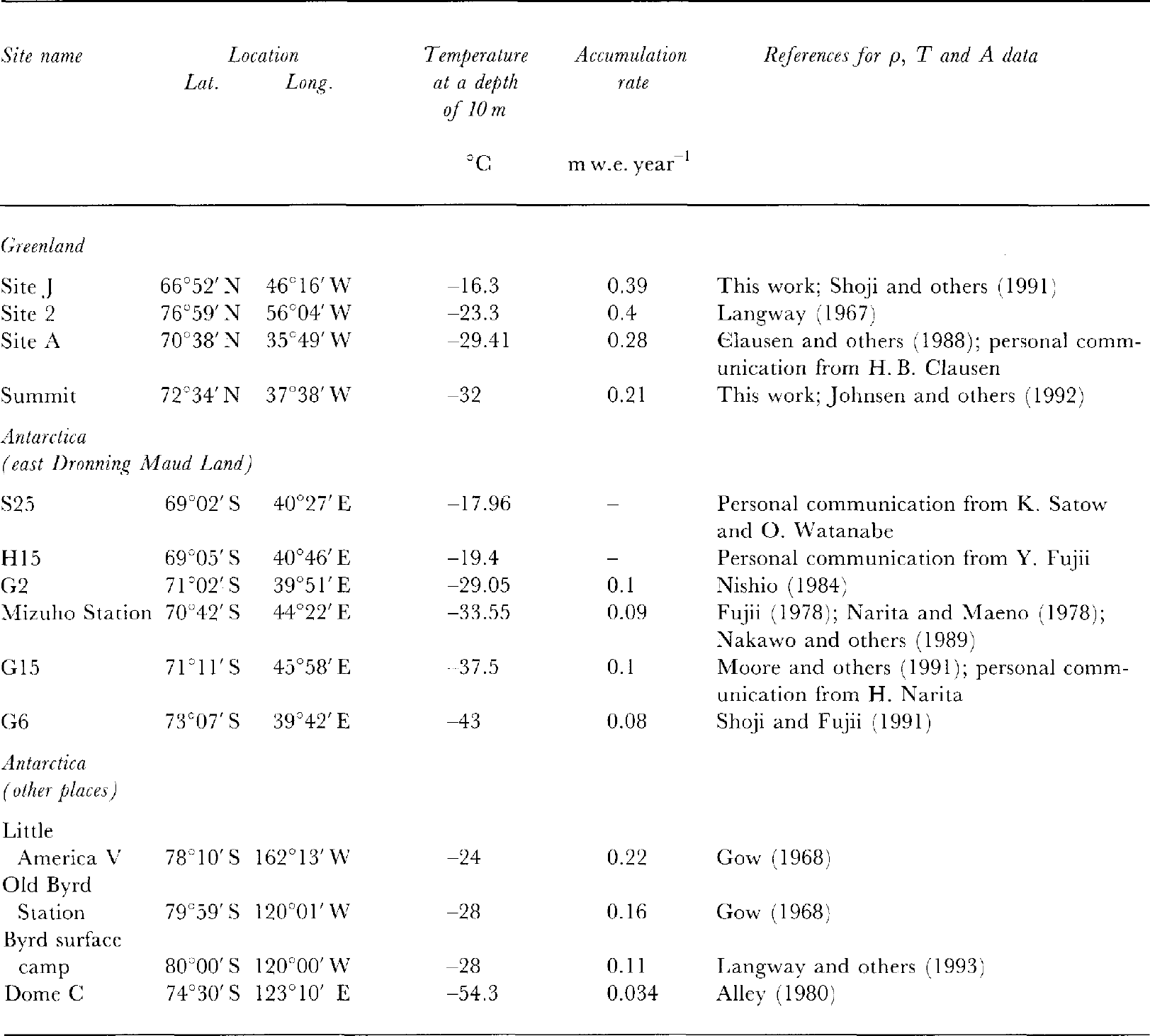
Depth-density information was obtained from 14 sites in Greenland and Antarctica as shown in Table 1. The 10m depth firn temperatures of the borehole range from-54.3° to -16.4°C and annual accumulation rates rangefrom 0.034 to 0.39 m year 1 in water equivalent. Thedata scatters in bulk-density values are generally ±0.005 Mgm-3 for those from Summit, S25, H15, S25, G15, G6,Byrd surface camp and Dome C. On the other hand, thedata scatters for siteJ, site 2, site A, G2, Mizuho, LittleAmerica V and Old Byrd Station are within ±0.003 Mgm-3, since the densities were determined more precisely by a volumetric method. The reliabilityof 10 m depth temperatures is generally ±0.1°C or better.

A trial was made to find the most satisfactory valuesfor m and n in Equations (1) and (4) using the above depth-density profiles. Depth-density values from thesurface to the depth at which the density is 0.80 Mg m 3are used for the correlation-coefficient analysis.

Figure la shows the results of the linearity test forEquation (1) using different values of m. It is clear that correlation coefficients take the highest values around m = -2 (r = 0.98). Figure 2b shows the results for Equation (4) using different values of n. It was found that the correlation coefficients take the highest value from n = -1 to + 1 (r = 0.97 at n = 1; r = 0.98 al n = 0;r = 0.95 at n = 1). Thus, we obtain the followingequations, which are identical with Equations (7) and (8):

(9)
(10)

where C1, C2, D3and D4are constants.

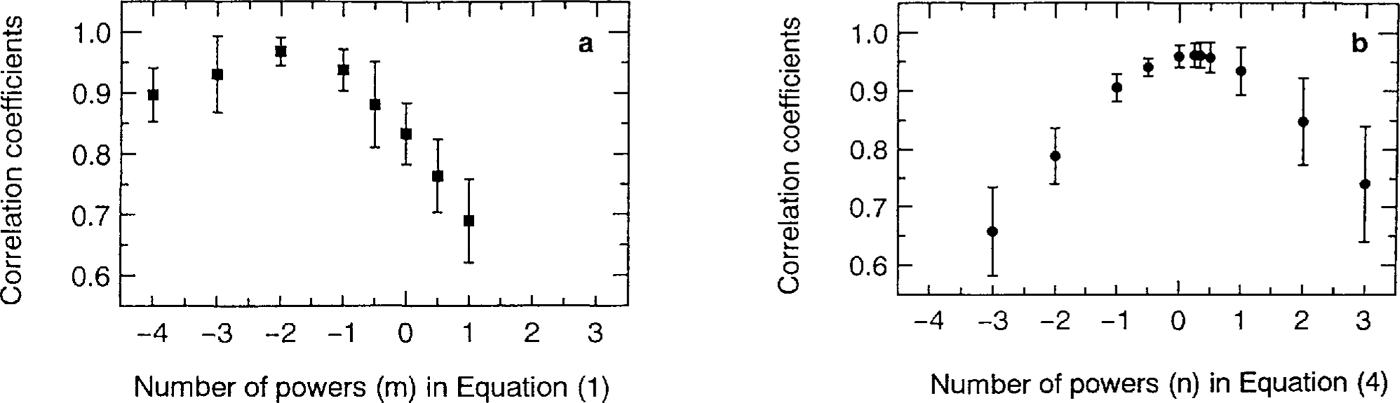
Fig.1 . The relation between values of powers and correlation coefficients with their standard deviations. Figure 1a shows the results for m in Equation (1) and Figure 1b for n in Equation (4).

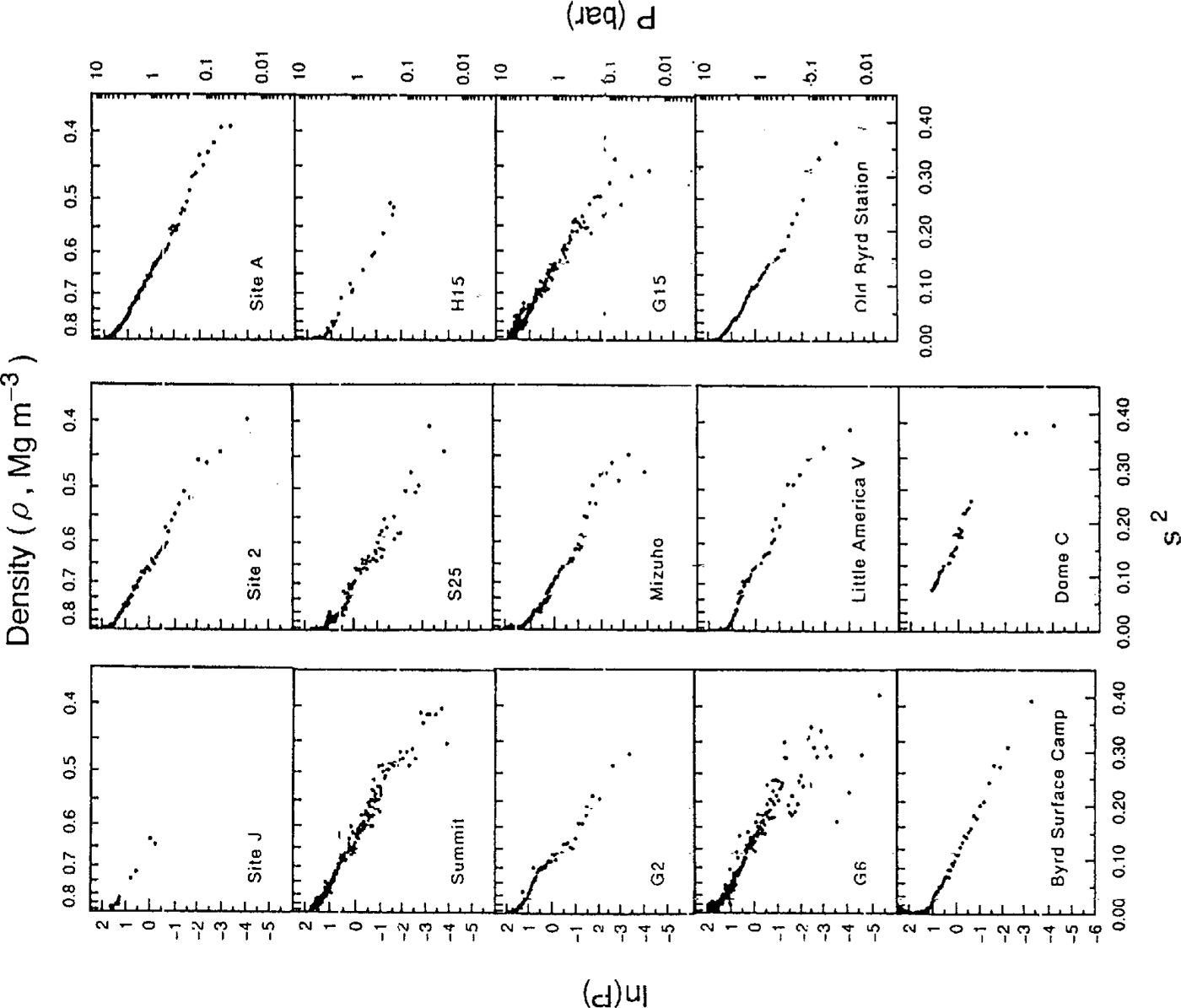
Fig.2 . Relations between ln(P) and s2for 14 sites in Greenland and Antarctica. P is an overburden pressure and s is the porosity of firn, where s =(ρi-ρ)/ρi.ρi is the bubble-free ice density and ρ is the firn density.

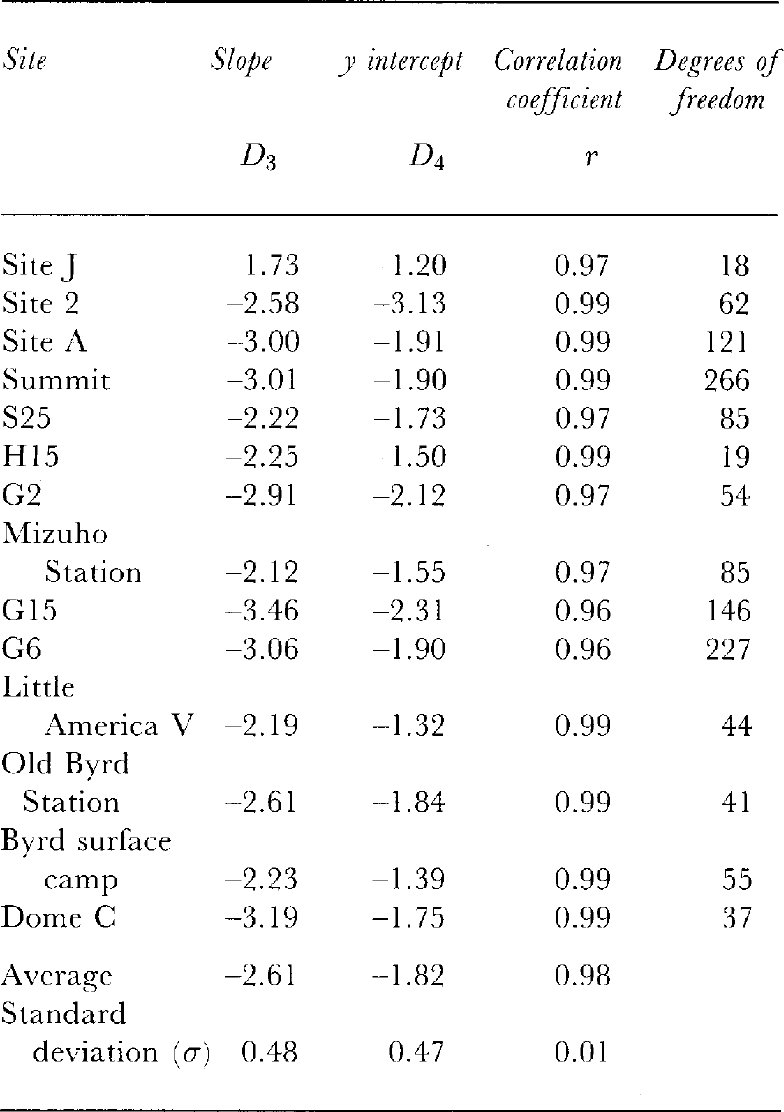
Figure 2 shows the relation between ln(P) and s2 for the 14 ice cores from Greenland and Antarctica. It is seenthat ln(P) and s2 have excellent linear correlation. Correlation coefficients, linear slopes (C1),Y intercepts(C2) and degrees of freedom are summarized in Table 2. The lowest correlation coefficient at G6 is due to datavariations in the surface-firn densities.

Figure 3 shows the relation between P and In(s) forthe 14 ice cores. It seems that most of the overburdenpressurecurves have a bend around a density of 0.50–0.60 Mg m-3. The linear-correlation analysis is summarizedin Table 3. The mean correlation coefficient forEquation (10), as shown in Figure 3(r = 0.98), is thesame as the mean correlation coefficients obtained for Equation (9) as shown in Figure 2 (r = 0.98).

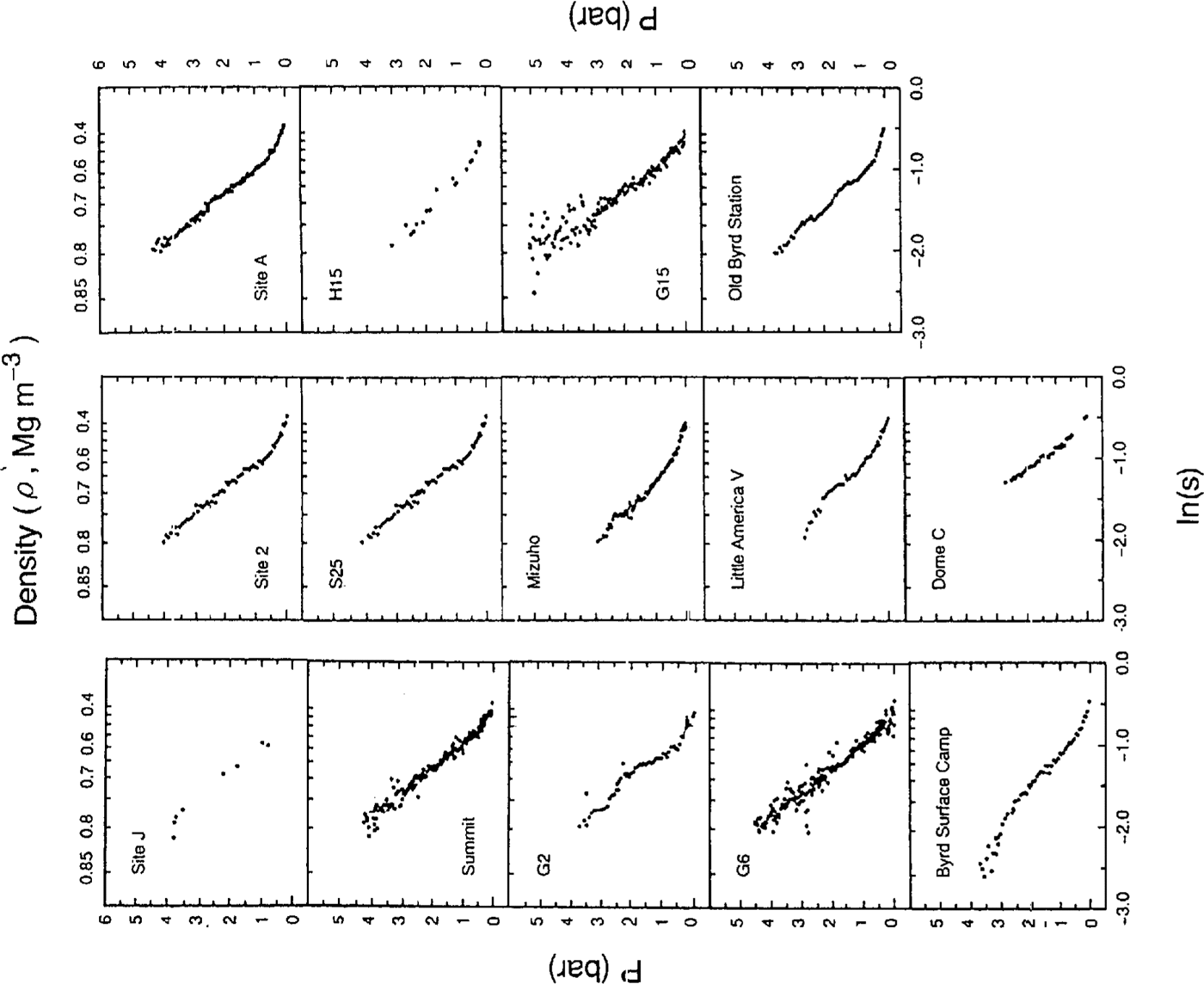
Fig.3 . Relations between P and In(.s) for 14 sites in Greenland and Antarctica

Table 1. Glaciological data and references for Greenland and Antarctic ice cores

4 Discussion

4.1 The relation between ln(P) and s2

The slope and y intercept for each site were investigated tofind the dependence on 10m depth firn temperature and/orannual accumulation rate. It was found that the y intercepts, C2, are well correlated with 10 m firn temperatures(r = 0.69) as shown in Figure 4. This is the onlymeaningful correlation. It is clear that the y intercepts of siteJ (SJ) and Mizuho (MZ) are shifted from other data. Thecorrelation coefficient without the above two sites is as highas 0.88. With this temperature-dependence of y interceptsfor 12 data points, we obtain the following equation:

(11)

where T is the 10 m depth firn temperature in K, P is anoverburden pressure in bar, ρ is the firn density in Mg m 3 and ρi is the bubble-free ice density at -20°C(0.919Mgm 3).

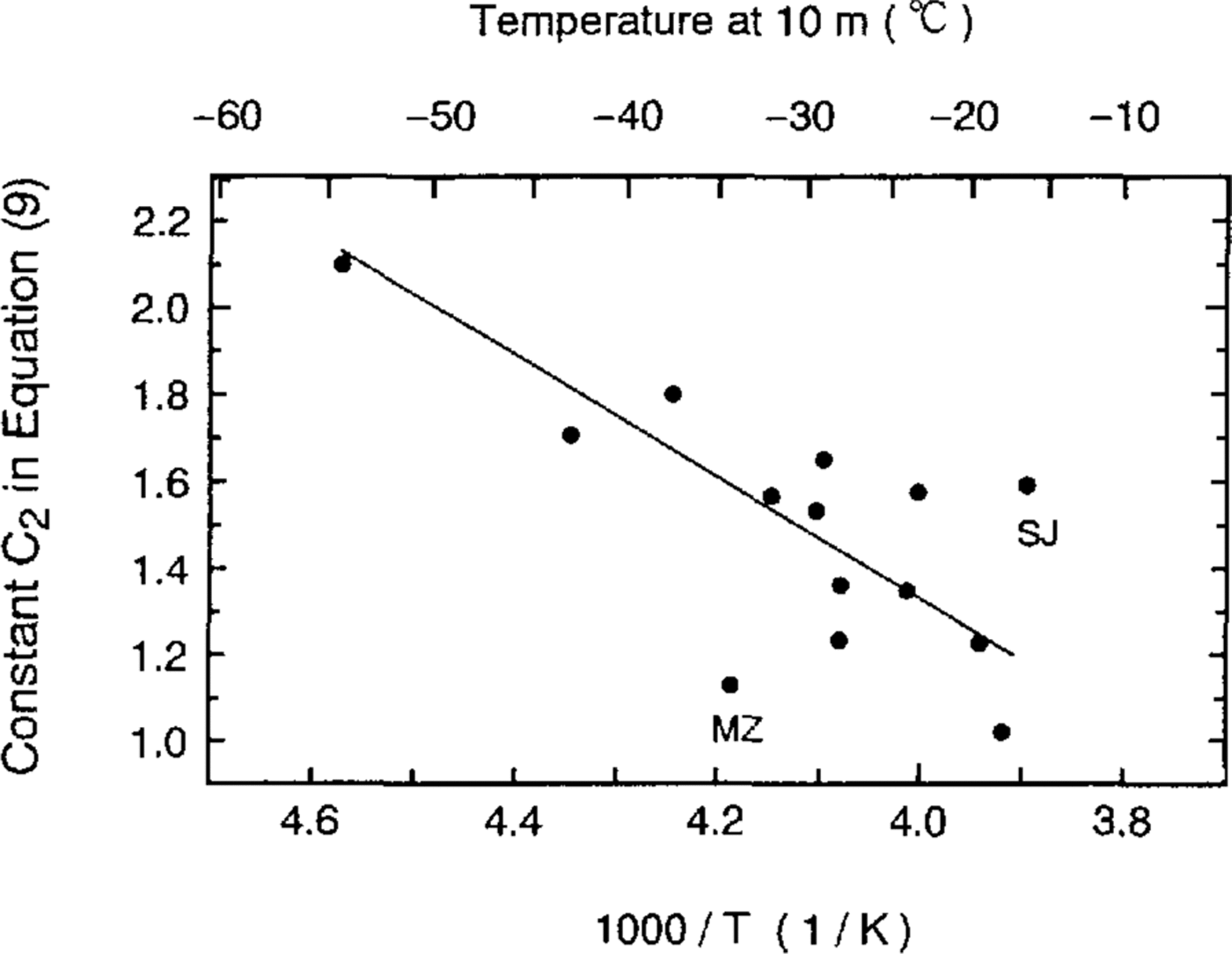
Fig.4 . Temperature-dependence of the y intercepts In Equation (9). SJ and MZ refer to ice coresfrom site J and Mizuho, respectively.

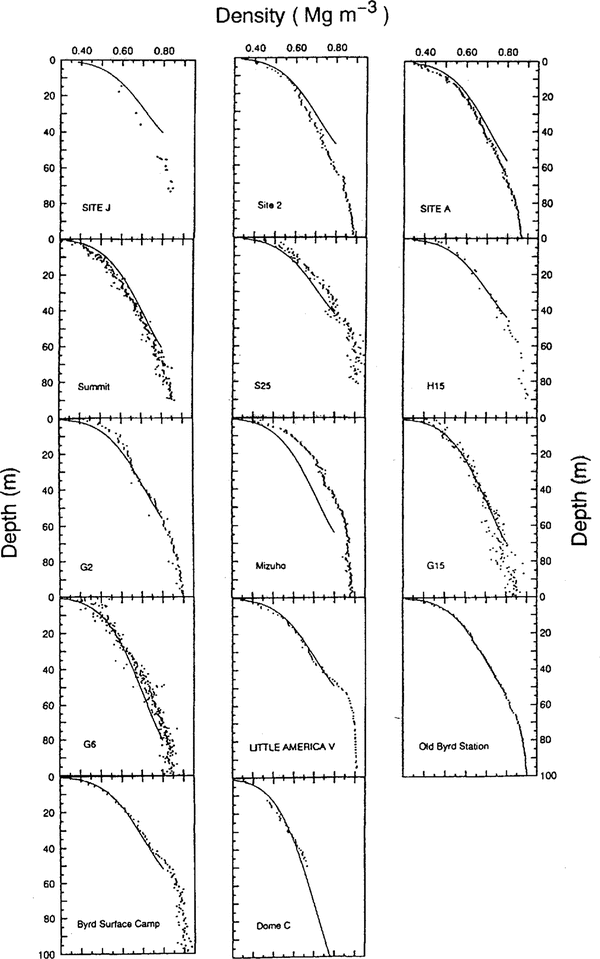
Comparisons of measured and calculated densityprofiles with Equation (11) are shown in Figure 5. It isseen that the site J and Mizuho ice-core data are shiftedsignificantly from the curves calculated from Equation(11). Site J is located in a percolation zone of theGreenland ice sheet Reference Watanabe and Fujii(Watanabe and Fujii, 1989) and the core contains 16.1% by volume of melt features (paper in preparation by Kameda and others).

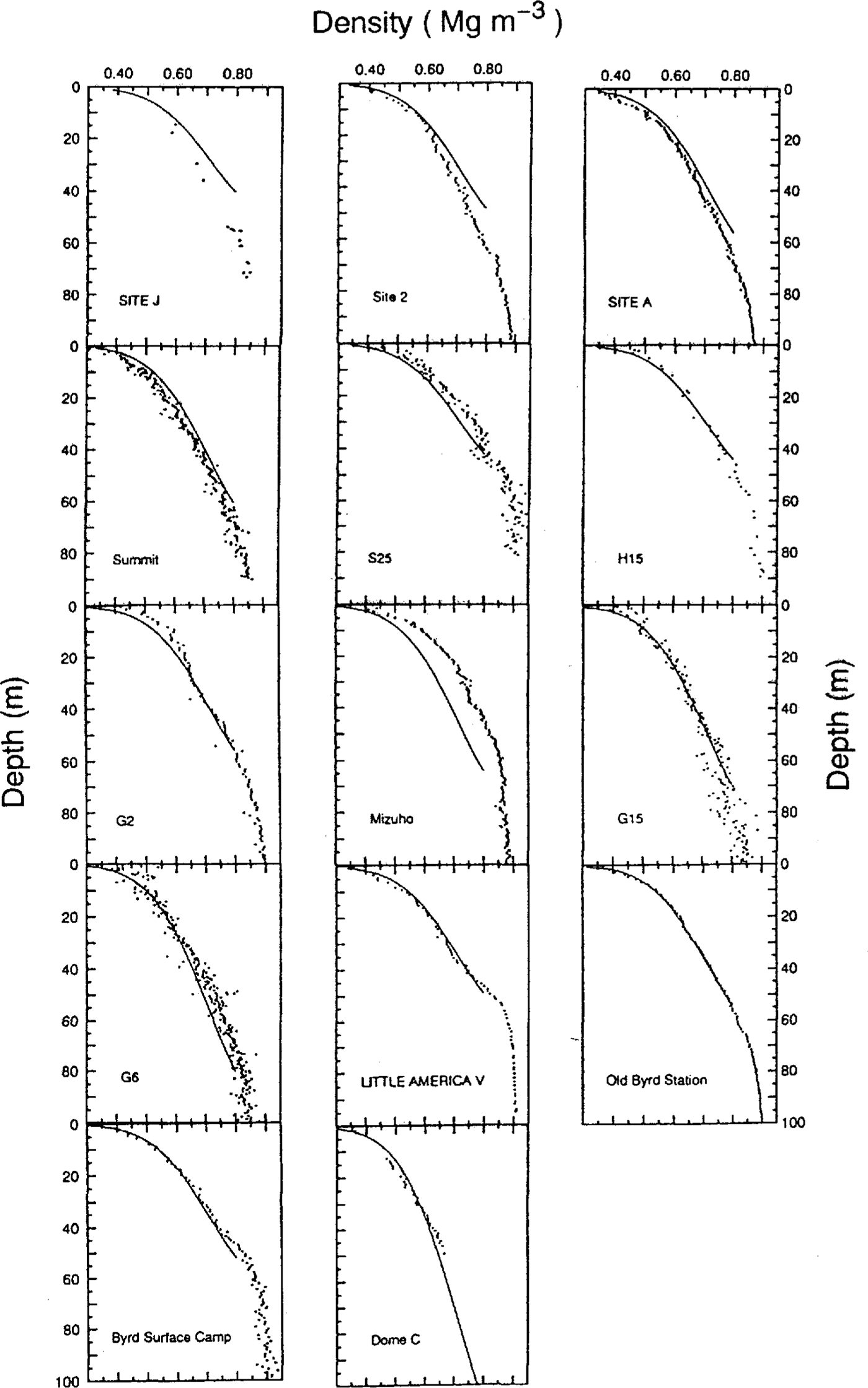
Fig.5 . Comparisons between measured density values (dots) and calculated profiles (lines). The calculated profiles areobtained from Equation (11).

Thus, refrozenwater around the grains can strengthen the grain bondingwhich may result in a delay in grain settling in the upper firn. On the other hand, Mizuho Station is located in acharacteristic area where an hiatus in snow deposition hasbeen studied Reference Watanabe, Kato and Satow(Watanabe and others, 1978). Katabaticwinds produce denser snow/firn layers at the surfacearound this area. This may cause a higher density valuefor the Mizuho ice core.

Standard deviations of measured densities from the calculated densities in 14 ice cores arc 0.02 Mg m-3 onaverage (i.e. 3.2% accuracy). The standard deviations inthe site J and Mizuho ice cores are 0.05 Mg m-3 and0.06 Mg m-3, respectively. These disagreements aremainly from C2 values at site J and Mizuho. That is,the agreement could be improved considerably, if theinitial density value is adopted instead of T in Equation (11) for each site.

Table 2. Slopes, y intercepts, correlation coefficients and degrees of freedom for the relation in Equation (9)

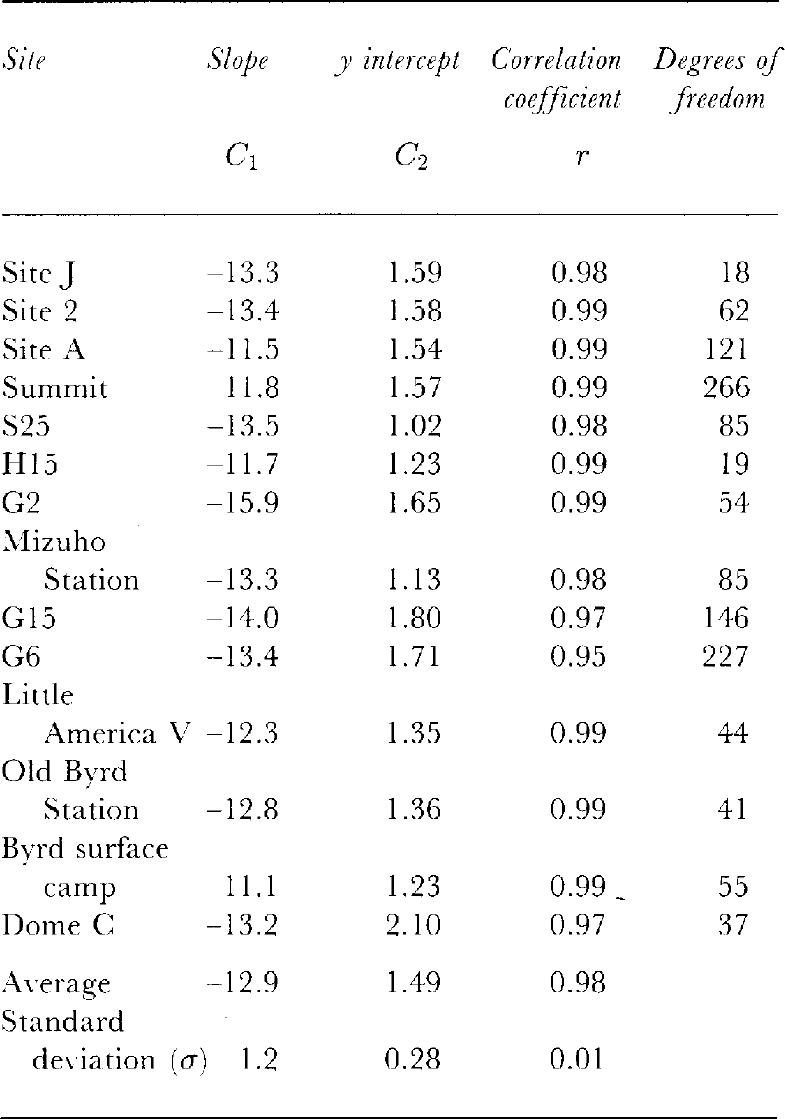
Table 3. Slopes, y intercepts, correlation coefficients and degrees freedom for the relation in Equation (10)

4.2 The relation between P and In(s)

The slopes and y intercepts were investigated to find thedependencies on the 10m depth firn temperatures and/orannual accumulation rates. It was found that the slopes,D3, are well. correlated with 10m firn temperatures(r = 0.72) as shown in Figure 6. For the same reasons as above, the values at site J and Mizuho could be deletedfrom Figure 6. The correlation coefficient between theslopes and the 10m depth firn temperatures has a slightlyhigher value of r = 0.76 if site J and Mizuho values are excluded. Using this temperature-dependence, we obtainthe following equation:

(12)

where T, P, ρandρi are the same as in Equation (11).

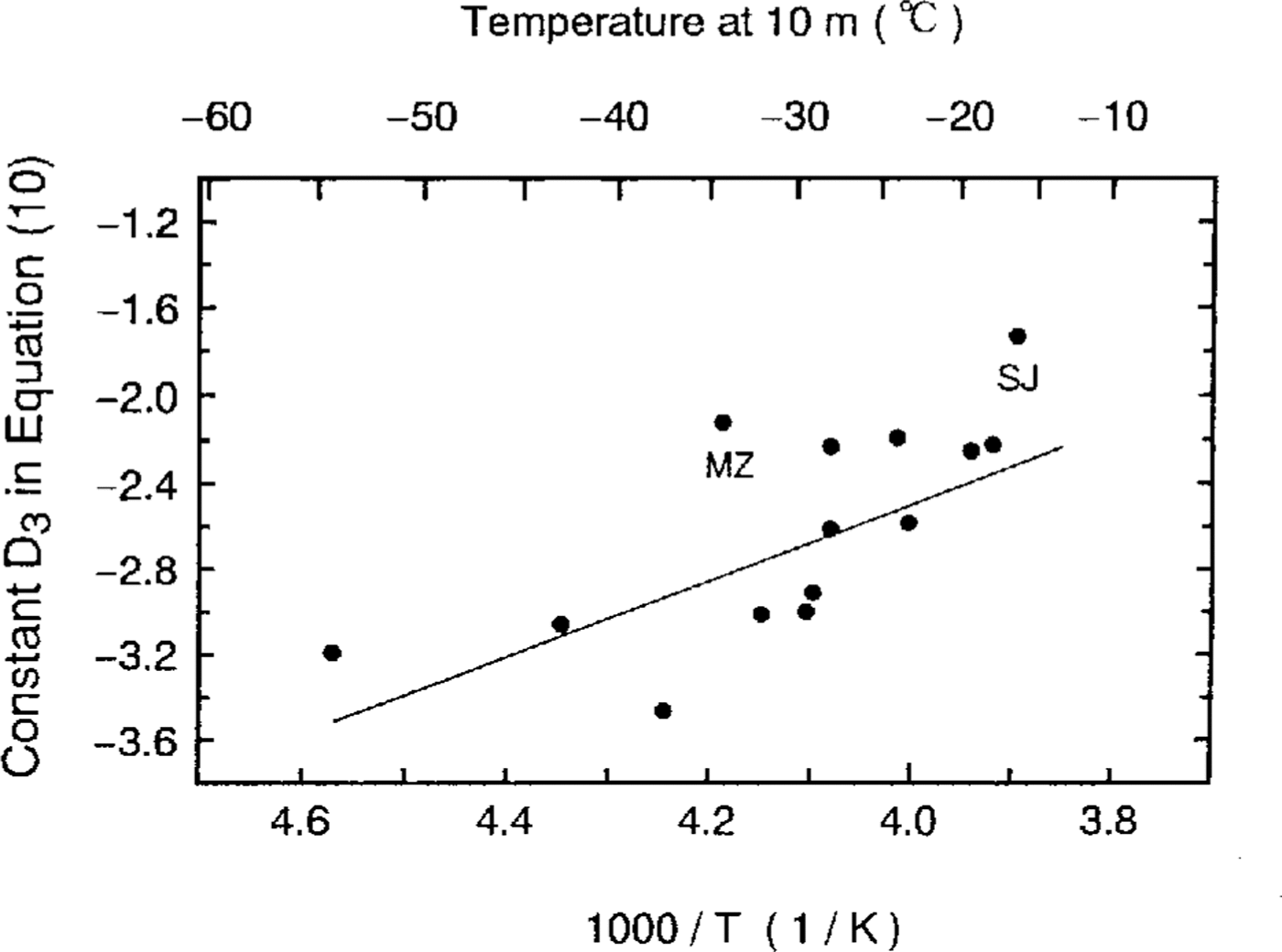
Fig.6 . Temperature-dependence of the slopes in Equation(10). SJ and MZ refer to ice cores from site J and Mizuho, respectively.

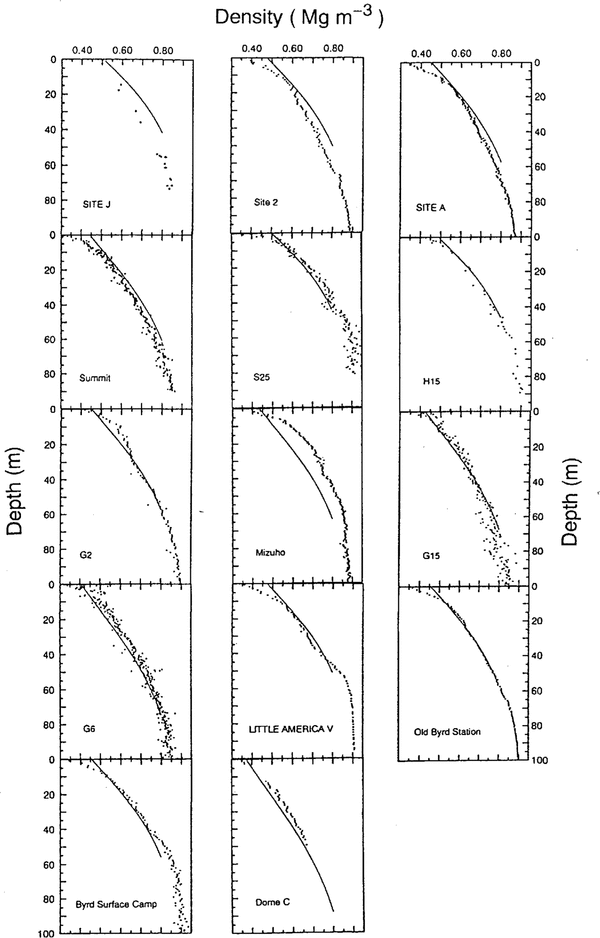
Comparisons of measured and calculated densityvalues using Equation (12) are shown in Figure 7.Again, it is seen that site J and Mizuho ice-core datahave significant shifts from the curves calculated from Equation (12). Average differences between the measuredand calculated densities in 14 ice cores are 0.03 Mg m-3(i.e. 4.7% accuracy). The average differences betweenmeasured and calculated values for site J and Mizuho icecores are both 0.06 Mg m-3, which is approximately thesame magnitude as for the case using Equation (II).

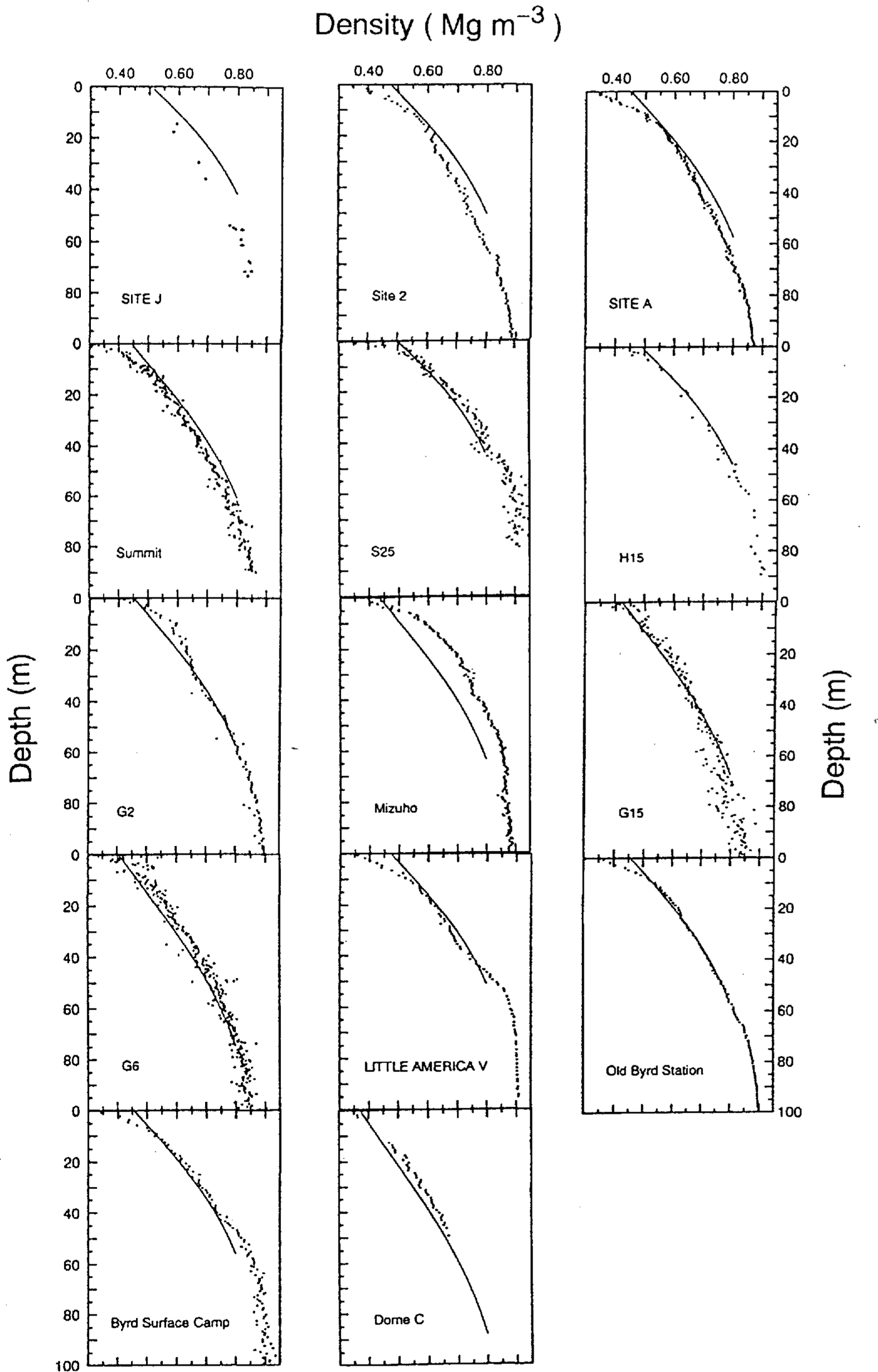
Fig.7 . Comparisons between measured density values (dots) and calculated profiles (lines). The calculated profiles areobtained from Equation (12).

Conclusion

These findings suggest that firn density can be determinedprimarily by overburden pressure; firn temperaturecontributes to a lesser degree, as expressed by Equations (11) and (12). That is, the validity of the equationproposed suggests that overburden pressure is the mostdominant factor in the densification process. Apparently,age-dependency is not as strong as expected previously for sites in a percolation zone or hiatus-observed area,each initial density at the surface should be taken intoaccount for a better fit with the measured density data.

Acknowledgements

We should like to thank Drs Y. Fujii, H. Narita, F. Nishioand K. Satow for providing unpublished depth-densitydata. The recovery of site J and Summit ice cores wassupported by a grant-in-aid for International ScientificResearch from the Japanese Ministry of Education, Science and Culture. We acknowledge logistic supportfrom GRIP members at Summit, Greenland. Ice cores from east Dronning Maud Land, Antarctica, wererecovered by the 23rd, 24th, 25th, 26th, 27th and 32ndJapanese Antarctic Research Expeditions.

Footnotes

The accurary oj references in lhe texl and in this list is the responsibility qf the authors, to whom queries should be addressed.

References

Alley, R. B. 1980. Densification and recrystallization offirn at Dome C,East Antarctica. Ohio State Univ. Inst.Polar Stud. Rep. 77.Google Scholar
Anderson, D. L, Benson, C. S. 1963. The densification and diagenesisof snow: properties, processes and applications. In Kingery, W. D. Ice and .snow. Cambridge, :MA, MIT Press, 391–411.Google Scholar
Bader, H. 1960. Theory of densification of dry snow on high polarglaciers. SIPRE Res. Rep. 69.Google Scholar
Bader, H. 1962. Theory of densification of dry snow on high polarglaciers H. SIPRE Res. Rep. 108.Google Scholar
Benson, C. S. 1962. Stratigraphic studies in the snow and firn of the Greenland ice sheet. SIPRE Res. Rep. 70.Google Scholar
Clausen, H.B, Gundestrup, N. S, Johnsen, S.J, Bindschadler, R, Zwally, J. 1988. Glaciological investigation in the Crête area, centralGreenland: a search for a new deep-drilling site. Ann. Glacial., 10, 10–15.CrossRefGoogle Scholar
Fujii, Y. 1978. Temperature profile in the drilled hole. Mem. Natl. Inst. Polar Res., Spec. 10, 169.Google Scholar
Gow, A.J. 1968. Deep core studies of the accumulation and densificationof snow at Byrd Station and Little America V, Antarctica. CRRELRes. Rep. 197.Google Scholar
Gow, A.J.. 1975. Time-temperature dependence of sintering inperennial isothermal snowpacks. International Association of HydrologicalSciences Publication 114 (Symposium at Grindelwald, 1974-SnowMechanics), 25–41 Google Scholar
Herron, M, M. and Langway, C. C. Jr. 1980. Firn densification: anempirical model. J. Glacial., 25(93) 373–385.10.1017/S0022143000015239CrossRefGoogle Scholar
Johnsen, S.J.. and 9 others. 1992. Irregular glacial interstadials recorded ina new Greenland ice core. Nature, 359 (6393), 311–313.CrossRefGoogle Scholar
Kojima, K. 1964. Densification of snow in Antarctica. Antarct. Res. Ser., 2, 157–218.Google Scholar
Langway, C. C. Jr. 1967. Stratigraphic analysis of a deep ice core from Greenland. CRREL Res. Rep., 77.Google Scholar
Langway, C. C, Shoji, H Jr., Mitani, A.. and Clausen, H. B.. 1993 Transformation process observations of polar firn to ice. Ann. Glaciol., 18. 1119–202.10.1017/S0260305500011502CrossRefGoogle Scholar
Ling, Chi-Hai. 1985. A note on the density distribution of dry snow. J.Glaciol., 31 (108), 194–195.CrossRefGoogle Scholar
Moore, J. C, Narita, H., Maeno, N. 1991. A continuous 770-year record of volcanic activity from East Antarctica. J. Geophys. Res., 96(D9), 17,353–17,359.CrossRefGoogle Scholar
Nakawo, M, Ohmae, H, Mishio, F, Kameda, T. 1989. Dating theMizuho 700-m core from core ice fabric data. Proc. NIPR Symp. PolarMeleorol. Glaciol., 2, 105–110.Google Scholar
Narita, H, Maeno, N. 1978. Compiled density data from cores drilled at Mizuho Station. Mem. Natl. Inst. Polar Res., Spec. Issue., 10 136–158.Google Scholar
Nishio, F. 1984. Stratigraphy and density data from ice core drilled atG2 grid station. JARE Data Rep. 94 (Glaciology 10) 64–83.Google Scholar
Robin, G, de Q. 1958. Glaciology III. Seismic shooting and relatedinvestigations. Norwegian-British-Swedish Antarctic Expedition., 1949–1952.Google Scholar
Schytt, V. 1958. Glaciology H. Snow studies at Maudheim. Snowstudies inland. The inner structure of the ice shelf at Maudheim asshown by core drilling. Norwegian-British Swedish Antarctic Expedition. 1949-52. Sci. Results., 4(2A), 1–64.Google Scholar
Shoji, H, Fujii, Y. 1991 Preliminary study of the G6, Antarctic icecore. (Abstract.) Pror. NJPR Symp Polar Meteorol. Glaciol. 4, 135.Google Scholar
Shoji, H, Clausen, H. B. and Kameda, T. 1991. Accumulation rate atSite-J and Dye-2, Greenland. Bull. Glacier Res., 9, 85–88.Google Scholar
Watanabe, O. and Fujii, Y.. 1989. Outline of the Japanese ArcticGlaciological Expedition in 1989 (JAGE 1989). Bull. Glacier Res., 8. 103–106.Google Scholar
Watanabe, O, Kato, K.. and Satow, K.. 1978. Stratigraphic analyses offirn and ice at Mizuho Station. Mem. Natl. Inst. Polar Res., 10. 25–47.Google Scholar
Figure 0

Fig.1 . The relation between values of powers and correlation coefficients with their standard deviations. Figure 1a shows the results for m in Equation (1) and Figure 1b for n in Equation (4).

Figure 1

Fig.2 . Relations between ln(P) and s2for 14 sites in Greenland and Antarctica. P is an overburden pressure and s is the porosity of firn, where s =(ρi-ρ)/ρi.ρi is the bubble-free ice density and ρ is the firn density.

Figure 2

Fig.3 . Relations between P and In(.s) for 14 sites in Greenland and Antarctica

Figure 3

Table 1. Glaciological data and references for Greenland and Antarctic ice cores

Figure 4

Fig.4 . Temperature-dependence of the y intercepts In Equation (9). SJ and MZ refer to ice coresfrom site J and Mizuho, respectively.

Figure 5

Fig.5 . Comparisons between measured density values (dots) and calculated profiles (lines). The calculated profiles areobtained from Equation (11).

Figure 6

Table 2. Slopes, y intercepts, correlation coefficients and degrees of freedom for the relation in Equation (9)

Figure 7

Table 3. Slopes, y intercepts, correlation coefficients and degrees freedom for the relation in Equation (10)

Figure 8

Fig.6 . Temperature-dependence of the slopes in Equation(10). SJ and MZ refer to ice cores from site J and Mizuho, respectively.

Figure 9

Fig.7 . Comparisons between measured density values (dots) and calculated profiles (lines). The calculated profiles areobtained from Equation (12).