The ice-filled caldera of Mount Wrangell, Alaska, provides an unusual opportunity to examine the interaction between a glacier and an active volcano. The caldera acts as a giant calorimeter, preserving a rough balance between snow precipitation at the glacier surface and bottom melting. In April 1982 we sounded the glacier using an airborne 840 MHz pulsed radar (Narod B B, Clarke G K C 1983 UHF radar system for airborne surveys of ice thickness. Canadian Journal of Earth Sciences 20(7): 1073–1086). The data were recorded on magnetic tape, then computer processed and plotted as depth, rather than time, sections.

In addition to mapping ice thickness, we detected extensive internal layers presumed to have been deposited during past eruptions of Mount Wrangell. The challenge of interpreting these internal reflectors inspired us to develop a unified interpretation model that incorporates both glaciological measurements and phenomenological equations for firn and ice. The interpretation model yields the variation with surface-normal depth z of temperature T, heat flux q, ice pressure p, density ρ, surface-normal component of flow velocity w, down-slope component of flow velocity u, depositional age ta, two-way wave travel time τ2, and two-way propagation loss P2. The following system of linear differential equations is integrated using the Runge-Kutta method:

1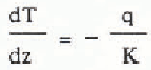

2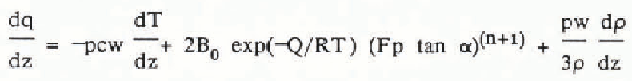

3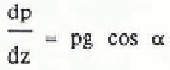

4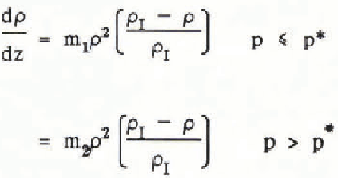

5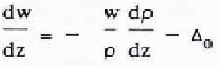

6

7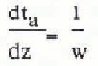

8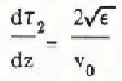

9 together with physical property relations such as the following 10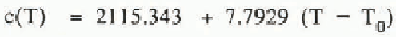

11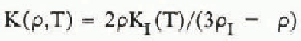

12

13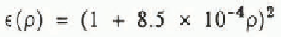

14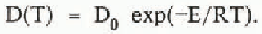

The boundary conditions on the integration variables are T(0) = Ts,T(h) = TM, p(0) = 0, ρ(0) =ρs, w(0) = ws, u(h) = uB, t a(0) = 0, τ2(0) = 0, and P2(0) = 0, where Ts is surface temperature, TM is bottom temperature, ρs is surface density, ws is surface-normal velocity measured at the glacier surface, and uB is sliding velocity. The remaining variables are thermal conductivity K, specific heat capacity c, flow-law constant B0, creep activation energy Q, universal gas constant R, shape factor F, surface slope α, flow-law exponent n, gravity acceleration g, empirical constants m1, m2, and p* from Benson’s firn-densification law (Benson C S 1962 Stratigraphie studies in the snow and firn of the Greenland ice sheet. SIPRE Research Report 70), ice density ρI, surface value of two-dimensional flow divergence Δ0 = (∂u/∂x + ∂v/∂y)s, relative dielectric permittivity ∈, free-space electromagnetic wave velocity v0, propagation loss rate D,T0 = 273.16 °K, thermal conductivity of ice K.I, loss-law constant D0, and activation energy for propagation loss E. The units of temperature and density in the above equations are respectively K and kg m−3.

Preliminary modelling has yielded an age-depth relationship for internal reflecting layers that roughly matches the known eruption record for Mount Wrangell and extends the volcanic history by more than 200 years. High signal absorption rates restrict interpretation of the caldera geometry. Reflections from the bed are not consistently detectable beyond a depth of approximately 350 m, suggesting a loss rate of 7–8 dB per 100 m of path length. The anomalous losses are attributed to abnormally high concentrations of ionic impurities and scattering sources.