Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Richards, Stephen J.
Currie, Iain D.
Kleinow, Torsten
and
Ritchie, Gavin P.
2020.
Longevity trend risk over limited time horizons.
Annals of Actuarial Science,
Vol. 14,
Issue. 2,
p.
262.
Basellini, Ugofilippo
Kjærgaard, Søren
and
Camarda, Carlo Giovanni
2020.
An age-at-death distribution approach to forecast cohort mortality.
Insurance: Mathematics and Economics,
Vol. 91,
Issue. ,
p.
129.
Blake, David
and
Cairns, Andrew J.G.
2021.
Longevity risk and capital markets: The 2019-20 update.
Insurance: Mathematics and Economics,
Vol. 99,
Issue. ,
p.
395.
Bergeron-Boucher, Marie-Pier
and
Kjærgaard, Søren
2022.
Mortality forecasting at age 65 and above: an age-specific evaluation of the Lee-Carter model.
Scandinavian Actuarial Journal,
Vol. 2022,
Issue. 1,
p.
64.
SriDaran, Dilan
Sherris, Michael
Villegas, Andrés M.
and
Ziveyi, Jonathan
2022.
A GROUP REGULARISATION APPROACH FOR CONSTRUCTING GENERALISED AGE-PERIOD-COHORT MORTALITY PROJECTION MODELS.
ASTIN Bulletin,
Vol. 52,
Issue. 1,
p.
247.
Basellini, Ugofilippo
Camarda, Carlo Giovanni
and
Booth, Heather
2023.
Thirty years on: A review of the Lee–Carter method for forecasting mortality.
International Journal of Forecasting,
Vol. 39,
Issue. 3,
p.
1033.
Richards, Stephen J.
2023.
Some comments on “A Hermite spline approach for modelling population mortality” by Tang, Li & Tickle (2022).
Annals of Actuarial Science,
Vol. 17,
Issue. 3,
p.
643.
Currie, Iain D
2023.
A black box approach to fitting smooth models of mortality.
Statistical Modelling,
Vol. 23,
Issue. 5-6,
p.
456.
Richards, Stephen J.
2024.
Robust mortality forecasting in the presence of outliers.
British Actuarial Journal,
Vol. 29,
Issue. ,
Lam, Ka Kin
and
Wang, Bo
2024.
Random cohort effects and smooth structures for mortality modelling and forecasting: A mixed-effects Gaussian process time series approach.
Communications in Statistics - Theory and Methods,
p.
1.
Wang, Yurou
Wang, Hui
Wang, Shengnan
Wind, Stefanie A.
and
Gill, Christopher
2024.
A systematic review and meta-analysis of self-determination-theory-based interventions in the education context.
Learning and Motivation,
Vol. 87,
Issue. ,
p.
102015.
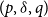 $(p,\delta, q)$
models with a fitted mean and
$(p,\delta, q)$
models with a fitted mean and 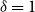 $\delta = 1$
or 2, identifiability extends to the forecast values of mortality; this extended identifiability continues to hold when some model terms are smoothed. The results are illustrated with data on UK males from the Office for National Statistics for the age-period model, the age-period-cohort model, the age-period-cohort-improvements model of the Continuous Mortality Investigation and the Lee–Carter model.
$\delta = 1$
or 2, identifiability extends to the forecast values of mortality; this extended identifiability continues to hold when some model terms are smoothed. The results are illustrated with data on UK males from the Office for National Statistics for the age-period model, the age-period-cohort model, the age-period-cohort-improvements model of the Continuous Mortality Investigation and the Lee–Carter model.