Introduction
In dairy sheep breeding schemes, the objectives of selection and the merit index have often been set up in an empirical way, forced by the genetic changes observed in a population (Barillet et al., Reference Barillet, Elsen and Roussely1986), or by a desire of including traits considered as useful in the breeding programmes. One of the traits to be improved in dairy sheep is the somatic cell count (SCC) of the milk (Rupp et al., Reference Rupp, Lagriffoul, Astruc and Barillet2003), as an indicator of mastitis and as a trait influencing milk quality. However, there are no published estimates of the economic impact of the genetic improvement of SCC in dairy sheep production, which is a key aspect for the decision process leading to its inclusion in the selection objectives and criteria. The purpose of this work is to compute the economic weight of the related trait somatic cell score in dairy sheep.
Traits
Mastitis
Mastitis is one of the main diseases in sheep. As such, it is of high economic importance in dairy sheep production, because it leads to lowered production, culling of animals, and poor milk quality. According to Bergonier and Berthelot (Reference Bergonier and Berthelot2003), “the term ‘mastitis’ means udder inflammation, whatever the origin, severity and evolution”, and “clinical mastitis is characterised by general signs (fever, anorexia, weakness, coma, etc.), or only local signs (udder inflammation and oedema, gangrena, asymmetry, sclerosis, abscesses, etc.) and functional signs (macroscopic or quantitative modifications of milk production). Subclinical mastitis is characterised by quantitative and qualitative functional modifications (especially an increase in somatic cell count)”. Most mastitis is of infectious origin, with different pathogens and forms involved. For recent reviews on mastitis in dairy sheep, see Bergonier and Berthelot (Reference Bergonier and Berthelot2003) and Bergonier et al. (Reference Bergonier, de Crémoux, Rupp, Lagriffoul and Berthelot2003). In this work, we will not consider mastitis itself because subclinical mastitis status of the ewe can not be directly determined. Rather, subclinical mastitis it is usually inferred from the SCC (Bergonier and Berthelot, Reference Bergonier and Berthelot2003).
Somatic cell count and somatic cell score
In dairy sheep, SCC is an indirect measure of subclinical mastitis infection. SCC is currently recorded in several milk recording schemes in dairy sheep, either systematically or experimentally (Astruc et al., Reference Astruc, Barillet, Fioretti, Gabina, Gootwine, Mavrogenis, Romberg, Sanna and Stefanake2004). The usual unit of expression of SCC is counts per millilitre. SCC shows a highly skewed distribution, which makes statistical analysis and the use of common selection tools (selection indices, BLUP) awkward. Thus, it is common to use a logarithmic transformation to achieve normality, with the new variable called somatic cell score (SCS).
Assuming a normal distribution for SCS assumes a log-normal distribution (e.g. Kendall and Stuart, Reference Kendall and Stuart1963) for SCC. A log-normal distribution is the distribution of a variable whose logarithm is distributed as a normal. If variable x follows a normal distribution, variable y = e x follows a log-normal distribution. The mean of the distribution of y is:
where μx and 
These properties are of interest for the following sections.
The most used logarithmic transformation was proposed by Ali and Shook (1980), as follows: SCS = log2 (SCC/105)+3. The logarithm is expressed in base two, which means that an increase of one in the SCS scale implies doubling in the SCC scale. Many studies exist on the genetic background of SCS in dairy sheep; for references, see Rupp et al. (Reference Rupp, Lagriffoul, Astruc and Barillet2003). The economic weight will be therefore calculated on the Ali and Shook (1980) SCS scale, as the simplest one, and the scale in which estimated breeding values are calculated and presented. Transformation to other logarithmic scales is straightforward considering the ratio between the scales.
Material and methods
Economics of SCC in dairy sheep
We have considered five different economic consequences of the genetic improvement of SCS and therefore of SCC:
Loss of milk during lactation
The loss has been described in the Latxa dairy sheep by Romeo and Ziluaga (Reference Romeo, Ziluaga and Arranz1998), to be about 40 ml/day per 1 − point increase of SCS. However, including this loss as related to genetics of SCS would cause the so–called double–counting (Groen et al., Reference Groen, Steine, Colleau, Pedersen, Pribyl and Reinsch1997a), as the genetic determinism of milk yield is already accounted for by considering the trait milk yield in the selection criteria. If there is an episode of severe mastitis, sheep is dried and its record is not considered for genetic evaluation, causing some bias, but clinical mastitis is difficult to relate to SCS. For completion, we point that the economic loss would be the loss in milk weighted by the price of the milk (0.92 € per l, as shown later). If the lactation length is 120 days, the value of the lost milk due to increase in SCS would be about 4.42 € per point of SCS.
Lower milk prices
As in cattle, the policy of dairy industries is to penalise milk prices if the SCS of the bulk tank milk within a certain period exceeds certain thresholds. There are a few penalisation systems depending on the factory, but most are very similar. We have chosen one of them which consists in paying, in relation to the standard price, +0.018 € per l if the SCC of the bulk milk is lower than 300 000; or, − 0.012 € per l if the SCC is higher than 750 000. This affects those farms who sell milk. There also other farms who produce cheese for sale.
Diminution of cheese yield and quality
This diminution is known (e.g. Jaeggi et al., Reference Jaeggi, Govindasamy-Lucey, Berger, Johnson, McKusick, Thomas and Wendorff2003; Albenzio et al., Reference Albenzio, Caroprese, Santillo, Marino, Taibi and Sevi2004) but very hard to quantify and for this reason we ignored it. There are two types of farms in the Latxa breed, according to their final product: cheese–farmers (those who elaborate home–made cheese and sell it), and milk–farmers (those who sell milk to cheese factories). This would affect cheese–maker farms, for which we will not be able to predict an economic weight for this concept. If penalties in milk price are according to losses in cheese yield in the factories, the economic weight should be similar.
Veterinary treatment
When a ewe is considered to be infected and if infection is not too severe (subclinical mastitis), the veterinary treatment consists of inoculation with antibiotic and a period of suppression of milk of about three days, in which milk can not be sold or used. The cost of treatment oscillates from 1.20 to 2 €; we retained a cost of 2 € to be conservative. The suppressed milk was considered to be three times the daily average production, which is around 800 ml. This makes 2.4 l of milk, which, multiplied by a milk price of 0.92 € per l (Legarra et al., Reference Legarra, Ramón, Ugarte and Pérez–Guzmán2007) makes a total of 4.21 € per treatment.
Detection of mastitis status depends on level of SCC. Romeo et al. (Reference Romeo, Ziluaga and Marco1998) set the thresholds for the Latxa breed in 140 000 (doubtful) and 340 000 (infected). In practice, a rule of thumb is to consider a sheep to be infected if the SCC of one test day (TD) surpasses 200 000. This rule has been used in this work. Other rules (e.g. dynamic rules, which consider the change of SCC during lactations) and thresholds exist for different breeds (Bergonier and Berthelot, Reference Bergonier and Berthelot2003). They are rather dependent on management systems and prevalence of mastitis in the studied flocks.
Lower ability, leading to culling
One of the reasons for culling in dairy sheep is a high susceptibility to mastitis, as seen by recurrent clinical or subclinical mastitis problems. As explained by Barillet et al. (Reference Barillet, Rupp, Mignon-Grasteau, Astruc and Jacquin2001), symptoms of clinical mastitis are modification of the colour or consistency of the milk, hot swollen or painful udders, positives at the California mastitis test, and udder abnormalities. This is the second most important reason for culling (after low milk production) in the experimental Lacaune flock of La Fage (Barillet et al., Reference Barillet, Rupp, Mignon-Grasteau, Astruc and Jacquin2001). Recurrent high SCC is also cause of culling, but less frequent. We consider that this culling is involuntary, as it is forced by the presence of mastitis and not by the concept that the replacement ewe will be more profitable than the replaced one (which is the case for production traits).
Therefore, among all the economic consequences of high SCS, we have retained three: (a) the change in milk prices, (b) the cost of veterinary treatment and (c) involuntary culling due to mastitis. In setting up these economic consequences, we are assuming a management of the flock which is quite typical in the Latxa breed. Other farms or breeds may have different managements, e.g. reducing the number of drying–off treatments if there is a reduction in SCC, not treating ill animals, or using different culling strategies.
Profit functions
Separate profit functions were calculated for each of the three economical consequences of SCC presented above. Two of them are non–linear, as they depend on the probability of SCC, or SCS, or some aggregate trait, exceeding certain thresholds; therefore, the economic weight depends on the actual average of the population and the environmental variability of the trait. Analogous cases were presented by Hovenier et al. (Reference Hovenier, Brascamp, Kanis, Van der Werf and Wassenberg1993), Colleau and Le Bihan–Duval (Reference Colleau and Le Bihan–Duval1995), and Veerkamp et al. (Reference Veerkamp, Stott, Hill and Brotherstone1998).
Milk payment
Penalties exist for milk payments beyond certain thresholds of SCC in bulk milk tank (SCCflock milk). However, this not an individual measure, but an aggregate of many SCC phenotypes, which follow log–normal distributions. This poses some problems, as discussed by Veerkamp et al. (Reference Veerkamp, Stott, Hill and Brotherstone1998). The effect of changing the genetic background of one animal (or all the flock) is the average of a sum of log–normal distributions, which, moreover, will depend on present averages in the flock. Veerkamp et al. (Reference Veerkamp, Stott, Hill and Brotherstone1998) solved this problem by empirical simulation, sampling SCS records from the milk recording data.
The procedure is very similar to that discussed by Colleau and Le Bihan–Duval (Reference Colleau and Le Bihan–Duval1995), and presented in more detail by Dekkers (Reference Dekkers2003). Let all animals in the flock have an (individual) mean in the SCS scale of μSCS, being dependent of environmental (management) or other (genetic) effects. At the flock level, the expectation of SCC in the flock (i.e. the SCC in flock bulk tank milk) can be calculated, by the features of the log–normal distribution, as
where 

As we have shown, the expectation of the SCC of the flock bulk tank milk depends on the mean and variance of individual SCS. As such, this expression implies that SCC flock milk is constant, given those parameters. However, in practice there will be some variation (e.g. in different milkings) due to the fact that the number of ewes being milked (n) is finite. Therefore, the variable SCC flock milk follows the probability distribution of the average of n log-normal distributions. Let call this distribution f(SCC flock milk) which depends on n, μSCS and 
For a flock with given μSCS and 
evaluated at μSCS. The average profit, P, can be computed as
where m is the number of price categories and p i is the proportion in category i. The term p i can be calculated as the cumulative density function of f(SCC flock milk), that is:

where t(i) is the upper payment threshold for the i − th category (first and last threshold are zero and infinity). Colleau and Le Bihan–Duval (Reference Colleau and Le Bihan–Duval1995), and Dekkers (Reference Dekkers2003), could go a step further to avoid the computation of the derivatives and the cumulative density function, applying Leibnitz's rule to cancel out integrals and derivatives. However, applying the rule in this case was not possible. We computed the profit function by the Fenton–Wilkinson approximation and the derivatives by numerical methods, as explained in the Appendix. We assumed 150 animals being milked at the same time.
Veterinary treatment
The procedure is very similar to that discussed by Colleau and Le Bihan–Duval (Reference Colleau and Le Bihan–Duval1995), and presented in more detail by Dekkers (Reference Dekkers2003), and it is as follows:
Assume that an animal has an expectation for SCS of μSCS. On repeated measures of its phenotype, SCC will be expressed as a log–normal distribution, or, equivalently, SCS will be expressed as a normal distribution with mean μSCS and variance 
The percentage of treatments, p, can be calculated according to this distribution, and it will be:

where 
Let consider an increase in the breeding value, d. The new percentage of treatments, p 1, will be:

Accordingly, the economic weight of an increase of d will be (p 1 − p)c, where c is the cost of the treatment.
However, this is valid as far as one TD analysis is considered. On average, four TD are analysed within a given lactation. For a given lactation, they can be considered as the same trait, the only variation due to within–lactation variance. We can also consider that, once a sheep has been medically treated, there are no more outcomes of subclinical mastitis for that lactation. Therefore the risk of having an episode of subclinical mastitis in a given TD is:
p (having subclinical mastitis) × p(not having it previously), the last probability being
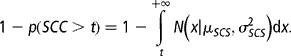
These probabilities have to be added for the four TDs considered, so that
where p i = (1 − p i − 1)p (SCC>t) and

Thus, the probability of an animal being infected at one of the four TDs in the lactation is a non–standard probability distribution. Derivatives of this distribution were computed by numerical methods, and weighted by the economic relevance for each category to obtain the derivatives of the profit function and the economic weight of SCS for veterinary treatment.
Involuntary culling
To include this concept in the profit function, the (genetic) relationship between clinical mastitis and SCC, and the culling policies for clinical mastitis or SCC should be known. The first one is not; in fact, as pointed out by Barillet et al. (Reference Barillet, Rupp, Mignon-Grasteau, Astruc and Jacquin2001), clinical mastitis usually occurs early in lactation, when SCC are not available. The culling policies are also poorly known.
To explore the bounds of the economic weight for this concept, we assumed a model based on genetic correlations. We define a conceptual trait ‘culled by mastitis’ (CBM), with a value of 1 if the ewe is culled because of mastitis, and zero otherwise. According to Barillet et al. (Reference Barillet, Rupp, Mignon-Grasteau, Astruc and Jacquin2001), this event is more related to clinical mastitis (93%) than to high SCC (7%), so we will assume CBM to be fairly similar to clinical mastitis. The genetic relationship between CBM and SCS will be defined by a more or less strong genetic correlation.
In dairy cattle, a value of 0.7 is a usual estimate of the genetic correlation between clinical mastitis and SCS (Carlén et al., Reference Carlén, Strandberg and Roth2004). Mastitis in small ruminants is quite different from cattle (Bergonier et al., Reference Bergonier, de Crémoux, Rupp, Lagriffoul and Berthelot2003), and lower correlations between CBM and SCS have to be considered. Different values (0, 0.5, 0.7, 0.9) of the genetic correlation between CBM and SCS were therefore tested.
The incidence of CBM thus may be related to the genetic background for SCS. According to Barillet et al. (Reference Barillet, Rupp, Mignon-Grasteau, Astruc and Jacquin2001), frequency of CBM = 1 (culling) was 5.3% in first lactation; we assumed it to be constant for all lactations. This is a rather strong assumption but there is no other information available. This value was assumed to hold for all levels of SCC of the flock, because Barillet et al. (Reference Barillet, Rupp, Mignon-Grasteau, Astruc and Jacquin2001) observed the same incidence for the two divergent lines in the La Fage experimental flock, which substantially differ in the average SCC. Phenotypic variance of the binomial distribution of CBM is therefore 0.053 × (1 − 0.053) = 0.05. Genetic variance, assuming a heritability of 0.05, would be 0.0025. Therefore, the regression of the breeding value of CBM on the breeding value of SCS is:
where σCBM,SCS is the genetic covariance between both traits and 
where r g is the genetic correlation between CBM and SCS. Therefore a genetic increase of one unit of SCS increases CBM in 0.12 times the genetic correlation; 0 for null genetic correlation, 5% for a genetic correlation of 0.5, 7.8% for a genetic correlation of 0.7, and 10.6% for a genetic correlation of 0.9.
Cost of culling is hard to compute in the presence of quota or when culling is voluntary (e.g. Colleau and Le Bihan–Duval, Reference Colleau and Le Bihan–Duval1995; Groen et al., Reference Groen, Van Arendonk, Goddard and Vollema1997b). This is not the case, as culling is involuntary and there is no quota. No correction for the different production in different lactations was applied. Economic data was taken from Legarra et al. (Reference Legarra, Ramón, Ugarte and Pérez–Guzmán2007). The average age of the ewe culled by mastitis was calculated considering the probabilities of being culled by mastitis (0.053) or by any other reason (this was set to 0.13 to mimic a culling rate of 0.18). The result is 2.76 lactations. The cost of the replacement ewe is the cost of raising the hogget (52 €), divided by 5.58 lactations, multiplied by the 2.82 lactations in which the new ewe is considered to replace the culled ewe. This gives an average cost of involuntary culling of 26 € per culled sheep. Notice that the cost of 52 € is rather low in relation to free market price for hoggets (which can be two or three times that amount). In the free market what is paid is also the cost of opportunity of having a genetically good flock and the installations in which to keep hoggets for sale. The 52 € have to be considered as the increased cost originated to the farm by breeding one more replacement hogget.
The former expression for the increased frequency of culled ewes (CBM), multiplied by a cost of 26 €, gives the economic weight, i.e. the change in profit due to a genetic change in SCS.
Overall
The overall economic weight was calculated as the sum of the three components already presented.
Parameters
We have calculated the economic weights for different values of μSCS (average SCS of the ewe), which in turn correspond to values of average SCC of the flock between 50 000 and 1 000 000 SCC per ml, which is the usual range of values in dairy sheep. The values of the variances (Legarra and Ugarte, Reference Legarra and Ugarte2005) are: additive genetic variance = 0.20, permanent environmental variance = 0.18, residual variance = 1.16.
Sensitivity analysis
To check the effect of the different thresholds, payment systems and prices, a few parameters were changed: (a) penalties for milk flock SCC were doubled; (b) thresholds for milk flock SCC were made more stringent (200 000 and 500 000 SCC per ml); (c) the number of sheep being milked was assumed to be 50 (c1) or 500 (c2); (d) cost of veterinary treatment was changed in +50% (d1) and − 50% (d2); (e) threshold for veterinary treatment was changed to 100 000 (e1) and to 300 000 (e2) SCC per ml.
The effect of different genetic correlations between SCS and CBM has already been noted. Increasing the cost of replacement would increase the economic weight in the same proportion.
Genetic gains
Theoretical genetic gains were calculated using selection index theory assuming a simplified breeding scheme considering different pathways of selection (see Legarra et al. (Reference Legarra, Ramón, Ugarte and Pérez–Guzmán2007) for details). Two traits, milk yield and SCS, were considered as sources of information for the selection indexes. Different selection indices were used based on different economic weights. The economic weight for milk yield was calculated by Legarra et al. (Reference Legarra, Ramón, Ugarte and Pérez–Guzmán2007). For SCS, we used two of the economic weights calculated in this study for SCS, as well as a desired gains pseudo–economic weight that will be shown later. Genetic gains were also calculated when the selection index only considers milk yield, to check the correlated responses for SCS. In the case of selection for milk yield, it was assumed that no information for SCS was used; this is according to a practical application (if SCS is not selected for, it is unlikely that it is used for genetic evaluation), and results in slightly lowered accuracies of the selection indexes.
Two scenarios were considered for the genetic parameters. Legarra and Ugarte (Reference Legarra and Ugarte2005) estimated in the Latxa breed heritabilities of 0.21 for milk yield and 0.13 for SCS, and a (favourable) genetic correlation of − 0.30. Rupp et al. (Reference Rupp, Lagriffoul, Astruc and Barillet2003) estimated in the Lacaune breed a genetic correlation that turns out to be unfavourable (between 0.08 and 0.18). The pseudo–economic weight was calculated to fix, under these conditions, the genetic change of SCS to zero.
Results
Economic weights
Results are shown in Figure 1 for the case where the genetic correlation between SCS and CBM is 0.7. The economic weights due to culling are zero for a null genetic correlation, and − 1.38, − 1.93 and − 2.49 € for genetic correlations of 0.5, 0.7 and 0.9 respectively. This economic weight is constant at different levels of SCC of the flock. This is the major part of the overall economic weight unless the average SCC of the flock is close to a pricing threshold.

Figure 1 Overall economic weight of somatic cell score (SCS) and its components for different levels of somatic cell count (SCC) of the flock. The assumed genetic correlation between ‘culling by mastitis’ and SCS is 0.7.
The absolute economic weight of SCS due to payment penalties is only relevant when the SCC level of the flock is close to the thresholds, because, at any other point, the probability of reaching any better payment threshold is almost null. In other words, when the average level of SCC is close to the thresholds, it is worth investing in genetic improvement of SCS because there is a high probability of milk being sold for a higher price. The absolute economic weight of subclinical mastitis treatments increases and then decreases. The reason is that, the closer we are to the threshold for treatment, the more treatments are saved by improving SCS. In other words, at low levels of SCC there are very few treatments to be saved, and at high levels of SCC all animals are theoretically infected and improving SCS does not save many treatments.
As a result, the overall economic weight of SCS is about − 3 to − 4 € per point of SCS per productive ewe in the flock in the range of common values of SCC in dairy sheep, except when the average SCC of the flock is around the payment thresholds, when it decreases down to − 9.50 € per point of SCS (at 303 000 counts per ml) and − 6.71 (at 754 000 counts per ml).
Sensitivity analysis
The different curves of economic weights obtained varying the different assumptions are shown in Figure 2. Increasing the payment penalties increases the economic levels, which also affect a wider range of average SCC of the flock. Using more stringent levels shifts the curve of economic weight to the left. Changing the number of animals changes the value of the economic weight and its position. Decreasing the number of animals makes that, for an increase in SCC, there is a higher risk of reaching a different quality threshold for SCC flock averages farther than the thresholds. This, in turn, decreases the maximum absolute value of the economic weight. A change in costs or thresholds for treatments changes the economic weights, but not in a great manner.

Figure 2 Sensitivity analysis of economic weights of somatic cell score (SCS) for different levels of somatic cell count (SCC) of the flock.
Genetic gains
The two economic weights chosen for SCS were − 4 € per point of SCS, which is the average economic weight for SCS, and − 9.50 € per point of SCS, which is the maximum absolute value. The economic weight for milk yield was 0.83 € per l (median of economic weight in milk–selling farms (Legarra et al., Reference Legarra, Ramón, Ugarte and Pérez–Guzmán2007)).
Genetic gains per year and associated increases in profit are shown in Table 1. Inclusion of SCS in the selection scheme leads to increased profits of 0.9% if the economic value is − 4 € per point of SCS and 2.6% if the economic value is − 9.50 € per point of SCS. The genetic change for SCS and the increase in profit is small for all possible economic weights and genetic parameters.
Table 1 Genetic gains (per year) and increase in profit considering different economic weights and genetic correlation (rg) between milk yield and somatic cell score (SCS)

† Economic weight for milk yield was 0.83 € per l.
‡ Desired-gains weight to constrain genetic change in SCS to zero.
§ The true economic weight to obtain the gain in profit was assumed to be − 4 € per SCS.
Imagine that the aim of a breeding programme, facing the unfavourable genetic correlation between milk yield and SCS, were to fix the level of SCS. In the case of unfavourable genetic correlation, a vector of pseudo–economic weights to attain this objective was 0.83 for milk yield and − 17.53 for SCC, for which the genetic gains are 3.66 for milk yield and 0 for SCS. These weights give four times more importance to SCC than the economic weights. The profit gain would decrease by 3% relative to the economically optimal set of weights ( − 4 € per point of SCS) or selecting for milk yield only. If the true genetic correlation is favourable, the decrease in profit gain is lower (around 2%).
Discussion
The economic weight of SCC oscillates between − 3 and − 4 € per point of SCS for most levels of SCC of the flock, with peaks close to the payment thresholds of about − 9 € per point of SCS. These are small figures for practical applications, as observed by the genetic gains, where the expected increase in profit ranges from 0.9% to 2.6%.
Different alternatives present different economic weights; however, it seems likely that economic weight for SCS are bounded from − 1 to − 10 € per point of SCS. Even in the higher bounds, the additional profit by including SCS in the breeding objective is not expected to be very high for two reasons: first, it is a low economic weight, as the unit of measure is rather high (a decrease of one in SCS means halving SCC); second, because the heritability and the genetic variances are low, the genetic improvement is slow. Quota systems or animal welfare concerns would increase the economic weight of SCS.
The low economic impact is quite independent of the assumed genetic correlation between SCS and milk yield. These are still a matter of discussion, as estimates in the Lacaune breed are unfavourable, whereas estimates in the Spanish breeds are favourable (e.g. Rupp et al. (Reference Rupp, Lagriffoul, Astruc and Barillet2003) and Legarra and Ugarte (Reference Legarra and Ugarte2005) and references therein) but we have shown that for different estimates either economic weights or a desired gains index are adequate, the latter being slightly economically worse. Yet one needs to be careful not to set too strong a restriction for the change in SCS, because the risk of greatly diminishing gains for milk yield exists depending on the true genetic parameters.
Drawbacks of the study are: first, some assumptions were taken in order to define profit functions. These include culling policies, culling rates, and thresholds for treatment and payment. Therefore the final results have to be considered as an approximation, based mainly on the management made in Latxa flocks. Second, the economic weight of culling due to mastitis was considered by an indirect reasoning, namely, the hypothetical correlations between SCC and the animal being culled by mastitis. We have tried to check some of these assumptions through the sensitivity analysis, which shows no big practical differences in genetic improvement. At any rate, the assumptions proved to be useful to set the range of values for the overall economic weight. A much more detailed study on culling policies and relation between SCS, SCC, mastitis and survival in dairy sheep is needed, and this should be one direction for future research.
Including SCS in dairy sheep breeding objectives has to be considered with caution, given its low economic weight and slow genetic improvement. The major cost of genetic improvement of SCS will be the implementation of SCS recording, which is usually associated with milk composition recording. Milk composition recording is being implemented in several countries (Astruc et al., Reference Astruc, Barillet, Fioretti, Gabina, Gootwine, Mavrogenis, Romberg, Sanna and Stefanake2004). In those cases, it seems reasonable to consider the inclusion of SCS in the breeding program. At any rate, it seems a better strategy at the beginning to first reduce mastitis/SCS problems by management (good hygienic and milking practices, drying–off treatments), which is quicker and cheaper than selection (Bergonier et al., Reference Bergonier, de Crémoux, Rupp, Lagriffoul and Berthelot2003). If changes in management are not useful anymore, selection might be a good option.
Acknowledgements
This work has been financed by project INIA RTA − 02 − 002 − C2. A. Legarra was partly financed by INIA, Spain. Manuel Ramón thanks the research fellowship given by INIA, Spain. We are grateful for the information on veterinary treatments provided by Javier García, Ane Garziandia and Rafael San Sebastián. We thank the referees for helpful comments.
Appendix
Computation of derivatives of an average of log–normal variables
Let 

The mean and variance of y are:
The distribution f(SCC flock milk) is the distribution of the average of a sum of n variables (individual SCC of daily yields) which are log–normally distributed with parameters μSCS and 

and approximated variance:

where w i are the weights for each variable; in this case, we assume that w i is constant and w i = 1/n.
However, the density of the log–normal distribution of SCCflock milk is parameterised in terms of the log of SCCflock milk (let call it LSCCflock milk), which follows a normal distribution. To find the appropriate parameters, one can solve as follows:


From the log–normal density function defined by these parameters, it is possible to construct the average profit, due to payment policies, for any given values of μSCS and 





