Introduction
The estimated mean neonatal lamb mortality rate in the UK is approximately 10% (Binns et al., Reference Binns, Cox, Rizvi and Green2002) and the proportion of the lamb crop that is lost early in life can be as high as 40% (Eales et al., Reference Eales, Small, Gilmour and Haresign1983). The large number of lambs lost early in life has a negative impact on both animal welfare and on the profitably of sheep farming. Despite its importance, lamb survival as a trait of the lamb has not been widely investigated. It is vital, therefore, to identify the genetic and environmental factors that influence lamb mortality in order to reduce the associated economic and welfare costs. Estimates of genetic parameters of lamb survival and its genetic correlations with other economically important traits are needed in order to include survival in the breeding programmes.
Early lamb survival is a complex trait that is influenced by the ewe's maternal ability and the lamb's capability for survival, in addition to the management practices and environmental variables at the time of birth and during the rearing period (Morris et al., Reference Morris, Hickey and Clarke2000; Southey et al., Reference Southey, Rodriguez-Zas and Leymaster2001). Most studies of lamb survival (e.g. Burfening, Reference Burfening1993; Olivier et al., Reference Olivier, Snyman, Van Wyk and Erasmus1998; Morris et al., Reference Morris, Hickey and Clarke2000) have used cumulative binary data analyses where animals are classified as alive or dead at the end of a period. However, the use of actual survival times through survival analyses enables the discrimination between lambs dying early or late in the period. Analysis of actual survival time also allows for the use of records from lambs that were culled or died within the period considered due to reasons not related to their viability, such as slaughter or accidental death, which is relatively common under extensive production systems. Estimates of heritability published in the literature for early lamb survival using binary data are mostly small and within the range of 0.00 to 0.09 (Burfening, Reference Burfening1993; Olivier et al., Reference Olivier, Snyman, Van Wyk and Erasmus1998; Matos et al., Reference Matos, Thomas, Young and Gianola2000). In addition, estimates of genetic correlations between survival and weight traits are still lacking in the literature.
The main objective of this study was to identify and estimate genetic and non-genetic explanatory factors affecting survival of Scottish Blackface lambs at different ages. The relationship of viability at birth with birth weight was also investigated and the genetic and environmental correlations between the two traits were estimated.
Material and methods
Data and traits
Survival data of Scottish Blackface lambs were obtained from two experimental farms in Scotland. One of the farms is located in the Pentland Hills in Midlothian where the climatic conditions are moderate. The other farm consisted of two flocks which were merged in 1997 and is located in west Perthshire which is colder and has harsher environmental conditions than the Pentland Hills. The breeding season was from the middle of November to the middle of December and the lambing season was therefore from the middle of April to the middle of May. Lambing occurred in fenced areas and the lambs were tagged and weighed within 24 h of birth. Ewes rearing singletons were sent back to the grazing hills with their lambs earlier (starting from about 1 week after lambing) than multiple rearing ewes which were kept with their lambs for longer times (several weeks) in smaller fenced grazing areas. Lambs were weighed at about 52 days and at weaning. Male lambs chosen for slaughter were separated from the rest of the animals and finished in better grazing areas. Animals were monitored daily and dead lambs were recorded with the cause of mortality.
A selection experiment with three genetic lines was initiated in 1997. A control and a selection line were created using a multiple trait selection index that included maternal and carcass traits. The third line, used for extension purposes, was created by introducing rams purchased from Blackface commercial flocks in the area, selected via visual appraisal only. In addition, the animals in the farms were genetically connected through participation in a Scottish Blackface sire referencing scheme by artificially inseminating 40 ewes per year in each farm with semen from two referencing rams selected from participating Scottish Blackface flocks. The distribution of animals among the lines were 22.02% in the selection line, 20.95% in the control line, 22.53% in the industry line, 3.27% used for sire referencing, and 31.23% in other carcass selected lines and crosses. Survival of the lambs was not selected on in any line. A summary of the lines and their performance are described by Conington and Murphy (Reference Conington and Murphy2003) and Conington et al. (Reference Conington, Bishop, Lambe, Bünger and Simm2006).
The data set consisted of about 15 000 survival records of lambs born from 1996 to 2005. The number of records for different survival traits and their distribution by farm are in Table 1. The pedigree of animals was traced back to the date of the establishment of the farms in 1991 and included relationships between 23 172 animals.
Table 1 Total number of records (N), distribution by farm (farm 1 and farm 2), number of sires (S), mortality rate (%) for viability at birth, and proportion of uncensored records (%) and mean age at death in days (Age) for postnatal survival traits
† Mean age at death for dead lambs.
Traits studied were lamb viability at birth, postnatal survival from 1 to 14 days, postnatal survival from 15 to 120 days, and survival from 121 to 180 days. Viability at birth was recorded as a binary trait (all or none trait) where lambs that survived for at least 24 h after birth were coded as 0, and lambs born dead or dying within 24 h of birth were coded as 1. The exact time of mortality within 24 h of birth was not available. Animals were required to be viable at birth (i.e. surviving more than 24 h) to be considered for the subsequent survival traits. Postnatal survival was defined as a continuous survival trait using the actual number of days survived before death or censoring. Data were considered censored if the lambs were still alive at the end of the specified period or died or were removed from the flock during the period due to reasons not related to their viability (i.e. accidents, slaughter or culling related to flock management).
Data on maternal behaviour were available and used to investigate the effect of this trait on lamb survival. Maternal behaviour score (MBS) was recorded on a 6-point scale measuring the dam's reaction and the distance the dam retreats from its lamb(s) when they are being handled for the first time within 24 h of birth (Lambe et al., Reference Lambe, Conington, Bishop, Waterhouse and Simm2001). Ewes retreating more than 10 m and not returning back to the lambs after handling were assigned the lowest score of 1 (1.14% of records). They were followed by ewes retreating more than 10 m but returning back after handling (score 2, 7.33%), ewes staying within 5 to 10 m (score 3, 15.41%), ewes staying within 5 m (score 4, 28.36%), and ewes staying within 1 m (score 5, 22.86%). Ewes staying with their lambs and making physical contact with them were given the highest score of 6 (24.90%).
Statistical analysis of viability at birth
Viability at birth was analysed with a linear mixed animal model (e.g. El Fadili and Leroy, Reference El Fadili and Leroy2001; Freking and Leymaster, Reference Freking and Leymaster2004) using the ASREML program, release 1.10 (Gilmour et al., Reference Gilmour, Gogel, Cullis, Welham and Thompson2002). Several models with different combinations of random effects were compared to determine the most suitable model to use. The random effects considered were direct and maternal additive effects and their covariance, maternal permanent (dam across years) and litter effects. The compared models had the same fixed effects and when nested (differed only in the number of random effects), they were compared using the likelihood ratio test (McCulloch and Searle, Reference McCulloch and Searle2000). The likelihood ratio test was based on chi-square distribution with degrees of freedom equal to the difference in the number of variance components to be estimated. Stram and Lee (Reference Stram and Lee1994) pointed out that this test is over-conservative when testing for values on the boundary of the parameter space. However, over-conservatism was not an issue here as all the results were highly significant. A model was considered to have a better fit to the data when it had a significantly larger log-likelihood value compared with another nested model (P < 0.05). The chosen model included random direct and maternal additive genetic effects and maternal environmental litter effects. The equation for the final linear mixed model used was:
where y is a vector of binary viability at birth observations, β is the vector of fixed effects, d is the vector of random animal additive genetic effects, m is the vector of random maternal additive genetic effects, c is the vector of random maternal litter effects, e is the vector of random residual effects, and X, Z1, Z2 and Z3 are incidence matrices relating observations with the respective effects. The assumption about the mean was E[y] = Xβ. The variances and covariances of random effects were assumed to be 
and Cov(d, m) = Aσdm, where A is the numerator relationship matrix, I is an identity matrix, and are the variances of the direct additive genetic, maternal additive genetic, maternal litter and residual effects, respectively, and σdm is the covariance between direct and maternal additive genetic effects. All other covariances between random effects were assumed to be zero. Random effects were assumed to have a multivariate normal distribution.
All biologically sensible explanatory factors and their two-way interactions were fitted as fixed effects and tested using the Wald test (Gilmour et al., Reference Gilmour, Gogel, Cullis, Welham and Thompson2002). Only significant effects (P < 0.05) were kept in the final model. Factors considered were type of birth (single, twin, or triplet), sex (male or female), age of dam (2, 3, 4, 5 or 6 and over 6 years), farm (two farms), year (1996 to 2005), genetic line (selection, control, industry, sire referencing and a group for other lines and crosses) and date of birth within year (starting from middle of April to middle of May) as a covariate. The effect of MBS on lamb viability at birth was tested by fitting MBS as a fixed effect in the model in a separate analysis. Estimates of differences between the mean mortality rates of different levels of fixed effects were obtained and tested using t tests adjusted for multiple comparisons using the Bonferroni correction.
The estimate of the total heritability was obtained as: where is the phenotypic variance (sum of variance and covariance components of all random effects in the model) and and σdm are as defined previously (Willham, Reference Willham1972). Observed estimates of direct, maternal and total heritabilities were transformed to an assumed underlying continuous normally distributed scale: transformed h2 = [h2p(1 − p)]/z2, where p is the proportion of animals in one of the binary categories and z is the ordinate of the standard normal density function corresponding to p (Dempster and Lerner, Reference Dempster and Lerner1950). Approximate estimates of standard errors of ratios of variance components were obtained using the inverse of the average information matrix (Gilmour et al., Reference Gilmour, Gogel, Cullis, Welham and Thompson2002).
Two analyses were performed to investigate the relationship of viability at birth with birth weight. First, birth weight of the lambs or predicted breeding values of birth weight were fitted as cubic orthogonal polynomial covariates in separate analyses of viability at birth using the models described previously. The order of the polynomials (cubic) was based on fitting the highest polynomial with statistical significance (P < 0.05). Then, to further investigate the relationship between birth weight and viability at birth, direct genetic and environmental correlations between the two traits were estimated using a two-trait analysis by a linear mixed model with random direct genetic and maternal litter effects. The fixed effects considered to be included in the model for birth weight were the same as for viability at birth and were chosen in the same way as in the analysis of viability at birth.
Statistical analysis of postnatal survival data
Postnatal survival traits were analysed using a Weibull proportional hazard model with the Survival Kit release V3.12 (Ducrocq and Sölkner, Reference Ducrocq and Sölkner1998). hi(t) for the ith lamb at day t given that the lamb was alive before that time point was modelled as:
***where β1 to βj are coefficients associated with explanatory variables xi1 to xij (fixed and random) for the ith lamb and h0(t) is the baseline hazard function with shape parameter ρ and scale parameters λ of the Weibull distribution. The Weibull model included random sire and maternal litter effects. The sire effect was assumed to follow a multivariate normal distribution while the maternal litter effect was assumed to follow a log gamma distribution and the effect was integrated out of the joint posterior density according to Ducrocq and Casella (Reference Ducrocq and Casella1996). The fixed factors tested and the procedure for deciding which effects to include in the final model were the same as described above for viability at birth but the number of lambs reared per ewe (type of rearing) was considered for inclusion as a fixed effect also. A separate analysis was also performed to test the effect of MBS on postnatal survival. As with viability at birth, this was done by fitting MBS as a fixed effect in the model.
Estimates for different levels of fixed effects with the Weibull model were obtained as hazard ratios, where the hazard rate for one level of a particular factor was calculated relative to the hazard rate for another level of the same factor. Standard errors of hazard ratios were obtained according to Collett (Reference Collett2003). Hazard ratios of different levels of fixed effects were tested using likelihood ratio tests (Ducrocq and Sölkner, Reference Ducrocq and Sölkner1998) and adjusted for multiple testing by Bonferroni correction. The shape parameter ρ of the Weibull model was estimated along with other parameters in the model. Estimates of heritability were obtained as where is the sire variance and π ≈ 3.1416 (Ducrocq and Casella, Reference Ducrocq and Casella1996). Standard errors of heritabilities were approximated using the Delta method (Searle et al., Reference Searle, Casella and McCulloch1992).
Results
Estimates of fixed explanatory effects for survival traits
Estimates of mean mortality rate at birth by sex, type of birth and age of dam are in Table 2. In addition to these factors, farm, year, and date of birth within year had significant effects (P < 0.05) on viability at birth. Male lambs had a higher mean mortality rate at birth than females. Twin born lambs had a significantly smaller (P < 0.05) mean mortality rate at birth than singletons and triplets. The mean mortality rate for triplets was significantly higher than that for singletons. The effect of age of dam was significant when comparing the mean mortality rate at birth of lambs from 2-year-old ewes with that of lambs from older ewes.
Table 2 Estimates of differences in mean mortality rates at birth and standard errors of differences between levels of sex, type of birth and age of dam, from the linear model analysis of viability at 24 h after birth
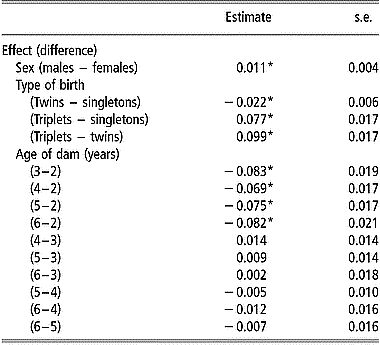
*Differences between mean mortality rates are significantly (P < 0.05) after Bonferroni correction to adjust for multiple testing.
Table 3 shows the estimates of hazard ratios for the significantly affected (P < 0.05) postnatal survival periods by the effect of sex, type of birth and age of dam. Sex of lambs had a significant effect (P < 0.001) on the hazard rate of mortality during all postnatal periods. Hazard ratios comparing males to females were always greater than 1, indicating that male lambs were at greater hazard during all postnatal periods compared with females. The largest difference in hazard ratio between the two sexes was during the postweaning period (from 121 to 180 days). The effect of type of birth on survival decreased with age of lambs as the hazard rate from 15 to 120 days and from 121 to 180 days was not affected by the type of birth of the lambs (P>0.05). Contrary to results observed for viability at birth, singletons had a significantly smaller hazard rate than twins during the postnatal period from 1 to 14 days. The hazard rate from 1 to 14 days was also significantly smaller for singletons than for triplets. Similarly, during the same period, the hazard rate for triplets was about twice as large as that for twin-born lambs.
Table 3 Estimates of hazard ratios and their standard errors for the effects of sex, type of birth, and age of dam on postnatal survival during given periods of age from Weibull model survival analysis
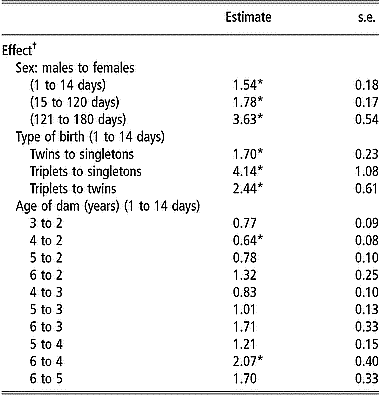
*Ratios are significantly different from 1 (P < 0.05) after Bonferroni correction to adjust for multiple testing.
† Only significant effects (P < 0.05) for different periods are presented.
Age of dam had a significant effect on the hazard rate from 1 to 14 days but not for survival from 15 to 120 days or from 121 to 180 days, thus following the same pattern as that for the effect of type of birth. Hazard rate from 1 to 14 days was larger for lambs born from younger or older ewes than for lambs born from ewes of intermediate age (3, 4 or 5 years) (Table 3). Lambs from 2-year-old ewes and those from 6-year-old ewes or older had a significantly larger (P < 0.05) hazard rate from 1 to 14 days than lambs from 4-year-old ewes. Ewes older than 5 years at the time of lambing had lambs with the highest hazard rate from 1 to 14 days, while 4-year-old ewes had lambs with the lowest hazard rate during the same period.
Dams with MBS = 1 had a significantly higher proportion of dead lambs at the time of birth (33%) than dams with a higher MBS (0.63%). On the other hand, dams with MBS = 1 had lambs with a lower hazard rate of postnatal mortality than others, although this difference was not statistically significant (P>0.05). Year of birth and farm had a significant effect on the hazard rate of lambs during most periods (results not shown), indicating possible variations in environmental and management factors across years and farms. Genetic line did not have a significant effect on any of the survival traits considered in this study.
Estimates of variance components
Estimates of variance components for viability at birth are in Table 4. The comparison between direct and maternal heritabilities shows that the maternal genetic effect had more influence on viability at birth than the direct genetic effect; estimates of direct and maternal heritability were 0.020 and 0.035 on the observed scale and increased to 0.054 and 0.095 on the transformed scale, respectively. There was a positive correlation between direct and maternal additive genetic effects (0.309), although it was not significantly different from zero (P>0.05). Estimates of the total heritability were 0.049 on the observed scale and 0.135 on the transformed scale. The maternal litter effect had the largest component of variance (19.2% of total variation) for viability at birth.
Table 4 Estimates of variance components and standard errors for viability at birth from linear model analysis
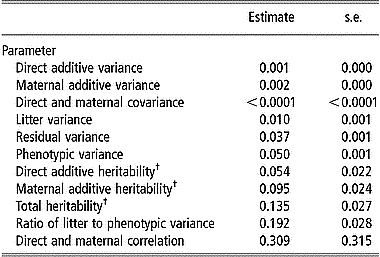
† Estimates were transformed to an assumed underlying continuous normally distributed scale.
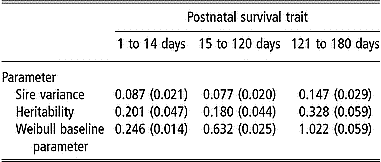
Estimates of variance components and the Weibull baseline parameter for postnatal survival traits are presented in Table 5. Estimates of sire variance resulted in estimates of postnatal survival heritability from 0.18 to 0.33. Standard errors of these estimates were noticeably small with ratios of the s.e. to the estimates of heritability ranging from 18 to 24%. Estimates of the Weibull baseline parameter ρ were less than 1 for the two preweaning periods (from 1 to 14 days and from 15 d to 120 d) and was close to 1 for survival from 121 to 180 days.
Table 5 Estimates of parameters (s.e.) from Weibull model survival analyses of postnatal survival from 1 to 14 days, from 15 to 120 days and from 121 to 180 days
Relationship of viability at birth with birth weight
Viability at birth had a cubic relationship with both birth weight and predicted breeding values of birth weight (Figures 1 and 2). Lambs with intermediate birth weights (ca. 3.5 to 4.0 kg) had lower mean mortality rate than lighter and heavier lambs. The lightest animals at birth had the highest mean rate of mortality, followed by the heaviest lambs. However, mortality rate had a positive unfavourable relationship with predicted breeding values of birth weight. Lambs with larger predicted breeding values for birth weight had a larger mean mortality rate than lambs with smaller predicted breeding values. Estimates of genetic and environmental correlations ( ± standard errors) of viability at birth with birth weight were 0.21 ± 0.08 and − 0.25 ± 0.04, respectively, and were both significantly different from zero. The positive sign of the genetic correlation means that the correlation is unfavourable, as the alive animals were coded 0 and the dead animals 1. On the other hand, the estimate of the environmental correlation was negative and favourable.
Figure 1 Relationship of mortality rate at birth with birth weight (kg).
Figure 2 Relationship of mortality rate at birth with predicted breeding values of birth weight (kg).
Discussion
Management and environmental conditions have an important effect on lamb mortality, indicating the potential for substantial improvement in lamb survival by improving lambing and rearing management practices. The effect of age of dam and type of birth on the hazard rate was more important at early than at later lamb ages. Single born lambs had higher mortality rate at birth but lower hazard rate afterwards (from 1 to 14 days). Morris et al. (Reference Morris, Hickey and Clarke2000) found generally similar effects, with a higher rate of mortality at birth for lambs born to 2-year-old dams and a lower preweaning survival for lambs born to 2- and 5-year-old dams. Therefore, to reduce early postnatal lamb mortality, particular attention should be paid to 2- and 6-year-old ewes and their lambs and to twin- and triplet-born lambs. To reduce mortality rate at birth, single born lambs and lambs born to 2-year old ewes should be preferentially treated.
The effect of sex was more important during the postweaning period, with male lambs at a much higher hazard rate. This trend may partially be attributed to the different management practices for males and females at this stage, since the majority of males are more intensively managed during the finishing period for slaughter. There was no significant effect of genetic line on any of the traits studied. The selection criteria used in the different lines were mainly for carcass and maternal traits and there was no direct selection on lamb survival as a trait of the lamb (Conington and Murphy, Reference Conington and Murphy2003; Conington et al., Reference Conington, Bishop, Lambe, Bünger and Simm2006).
There was a generally higher hazard rate at early stages in life than at later ages. This is based on the estimates of the Weibull baseline parameter (ρ), which was less than 1 at younger lamb ages and close to 1 at later ages. A Weibull baseline parameter less than 1 (as during the period from 1 to 14 days and from 15 to 120 days) means that the hazard of observing the event (mortality in this case) decreases from the beginning to the end of the period considered. A Weibull baseline parameter around 1 (as during the 121 to 180 days period) means that the hazard is constant over the period. Therefore, more attention should be given to lambs at younger ages for the overall improvement of lamb survival.
The extremely high proportion of dead animals at birth for dams with MBS = 1 may not imply that these dams provide less maternal care per se. This is because, dams are expected to pay less attention to lambs born dead than to those born alive and this may be the reason for assigning them the lowest MBS of 1, particularly for dams with dead singletons. Additionally, postnatal survival, which is expected to be positively related with the maternal ability of the ewes, was negatively but not significantly affected by MBS. Everett-Hincks et al. (Reference Everett-Hincks, Lopez-Villalobos, Blair and Stafford2005) studied the relationship between MBS and lamb survival to weaning and found that mortality was higher for lambs born to dams with higher MBS. Using data from the same farms as in this study, Lambe et al. (Reference Lambe, Conington, Bishop, Waterhouse and Simm2001) reported a higher proportion of lamb losses from birth to weaning as a trait of the ewe for dams with MBS = 1. These findings do not disagree with the current results, as the lamb losses in the Lambe et al. (Reference Lambe, Conington, Bishop, Waterhouse and Simm2001) study included those that were born dead, which were much higher for dams with MBS = 1, as was also shown in this study. It should be noted that MBS is not just a measure of the care and the attachment of the dam to her newborns but is also a measure of temperament of the ewe and its reaction to the presence of humans. It may be concluded that improving the MBS of the ewes, though found to be heritable by Lambe et al. (Reference Lambe, Conington, Bishop, Waterhouse and Simm2001), would not reduce postnatal hazard rate of lambs.
Estimates of heritability for all periods were significantly greater than zero. Similar results for survival at birth for Scottish Blackface were found by Riggio et al. (Reference Riggio, Bishop and Finocchiaro2005). The maternal genetic effects were more important than the direct genetic effect for viability at birth. Similar findings on the relative contributions of direct and maternal effects on different lamb survival traits were reported by Burfening (Reference Burfening1993), Morris et al. (Reference Morris, Hickey and Clarke2000) and Southey et al. (Reference Southey, Rodriguez-Zas and Leymaster2001). Using a Weibull model, Southey et al. (Reference Southey, Rodriguez-Zas and Leymaster2001) reported an estimate of heritability of 0.20 for lamb survival from birth to 120 days and from 120 to 365 days.
Viability at birth was analysed with a linear model as the likelihood must be approximated with non-linear modes. This is because of the lack of explicit expression for the likelihood for these models except as an approximate integral. The choice of the linear model for the analyses of this trait was based on the results of Matos et al. (Reference Matos, Thomas, Young and Gianola2000) comparing the analysis of binary lamb survival using linear and threshold models. They reported no significant differences in the predictive ability of the linear and threshold models. Similar conclusions were reached comparing correlations between breeding values predicted with linear and threshold models for the analysis of binary survival dairy cattle data (Boettcher et al., Reference Boettcher, Jairath and Dekkers1999).
Direct and maternal genetic effects for viability at birth were positively correlated but the estimate of correlation had a large standard error. The positive estimate of correlation suggest that dams with good genetic mothering ability (e.g. having larger uterine capacity) have better direct genetic potential to produce lambs with lower mortality rate at birth. This, if reliable, could enhance genetic improvement programmes aiming at improving lamb survival through selection. Obtaining accurate estimates of the correlation between direct and maternal genetic effects has proven to be difficult and data and model dependent. Robinson (Reference Robinson1996) showed, using simulated data, that negative estimates of correlation between direct and maternal genetic effects may be obtained in the absence of a true antagonism between them.
The environmental correlation between birth weight and viability at birth was in the favourable direction, indicating that the environmental factors increasing body weight at birth also reduce lamb mortality rate at birth. On the other hand, there was a positive unfavourable relationship between mortality rate at birth and predicted breeding values for birth weight. This relationship was also supported by the significant unfavourable genetic correlation of viability at birth with birth weight, as obtained in the bivariate analysis. There was also a non-linear relationship of birth weight of lambs with mortality rate, with intermediated birth weights having smaller mortality rate than lighter or heavier lambs. Consequently, selection for optimal birth weight, rather than maximum birth weight, should be practised when viability at birth and birth weight are to be improved simultaneously.
One possible explanation for the elevated mean of rate of mortality at birth for lambs with the smallest birth weights is hypothermia, whilst dystocia can be the cause of mortality for lambs with the heaviest birth weights. The heavier birth weight and its association with an elevated rate of mortality may also partially explain the higher rate of mortality at birth for singletons compared with twins. About 82% of the 5% heaviest lambs at birth were singletons, compared with 36% as the overall average of single born lambs in the data. In the same way, a higher proportion of the lightest lambs at birth was born as triplets compared with the proportion of triplets in the flocks. Similar results were found by Hall et al. (Reference Hall, Fogarty and Gilmour1995), Holst et al. (Reference Holst, Fogarty and Stanley2002) and Christley et al. (Reference Christley, Morgan, Parkin and French2003). They showed that birth weight had a non-linear relationship with hazard of mortality, with both lighter and heavier lambs at greater risk. Differences in management practices for ewes with singles and multiples during rearing period may also have contributed to the differences in survival of singles and multiples.
Conclusions
Lamb survival is affected by several environmental and management factors. Viability at birth and postnatal survival of Scottish Blackface lambs are heritable traits and all estimates of genetic variances found here were significantly greater than zero. Therefore, reduction of early lamb losses can be achieved by both management and genetic means. Survival of lambs is influenced by the genetic merit of both the lamb and its dam. Therefore, to achieve a higher selection gain for lamb survival, particularly at birth, selection indices should include lamb survival as a trait of the lamb and the dam together. Selection for improved viability at birth and birth weight should consider optimal rather than maximum birth weight.
Acknowledgements
The work presented here was funded by Defra (Department for Environment, Food and Rural Affairs), Scottish Executive Environment and Rural Affairs Department (SEERAD), British Wool Marketing Board (BWMB) and Meat and Livestock Commission (MLC). The authors would like to express sincere gratitude to Professors S. Bishop and G. Simm, to Drs C. Dwyer, L. Bunger, N. Man and W. Mekkawy for their valuable comments, to Professor V. Ducrocq and Dr Z. Chirinos for their assistance in running the Survival Kit programme, and to Dr N. Lambe, Miss A. McLaren and Mrs MSteel for collecting the field data.
