Article contents
The Quantification of Aristotle's Theory of Revolution
Published online by Cambridge University Press: 02 September 2013
Abstract

- Type
- Research and Methodology
- Information
- Copyright
- Copyright © American Political Science Association 1952
References
1 Barker, Ernest, trans. Politics (Oxford, 1948)Google Scholar, Bk. 5, Ch. 1, §11. The portions in brackets are comments of the translator. The term “sedition” in Barker's translation should be noted. Benjamin Jowett uses the term “revolution.” Barker prefers “sedition” as a translation of the Greek word stasis in order to do justice to the comprehensive meaning of stasis, which is not confined to armed rebellion. In view of the fact that the term “revolution” acquires a definite denotation in the Pareto-Davis theory, Barker's concept of “sedition” is helpful for the purpose of this inquiry.
2 Ibid., §12.
3 Ibid., Bk. 5, Ch. 5, §§1–4.
4 Ibid., Bk. 5, Ch. 6, §§2–3.
5 Ibid., §§6–7.
6 Ibid., Bk. 5, Ch. 7, §§1–2.
7 Ibid., §9.
8 Ibid., Bk. 5, Ch. 10, §14.
9 The Lives of the Noble Grecians and Romans, trans. Dryden, John and rev. Clough, Arthur Hugh (Library, Modern ed., New York, 1932), p. 104Google Scholar.
10 Pareto, Vilfredo, Cours d'économie politique (Lausanne, 1896–1897), Vol. 2, p. 306Google Scholar.
11 Representative samples were found by Pareto in the income distributions of the following countries and cities during the specified periods: England, 1843, 1880, and 1894; Prussia, 1852, 1876, 1881, 1886, 1890, and 1894; Saxony, 1880 and 1886; Florence, the city and county of Perugia, Aconia, Arezzo, Parma and Pisa combined, and other Italian cities in combination (no dates specified); Augsburg, 1471, 1498, 1512, and 1526; Peru, at the end of the 18th century (ibid., Vol. 2, p. 312).
12 Davis, Harold T., Political Statistics (Evanston, Ill., 1948), p. 185Google Scholar. Davis points out that this concept originally was proposed by Gini, C. in “Intorno alle curve di concentrazione,” Metron, Vol. 9, 1932, Nos. 3–4, pp. 3–76Google Scholar.
13 Political Statistics, p. 185. Davis uses a different notation in this formula; the parameter α. is symbolized by γ. In order to maintain a consistent set of symbols, the formula has been modified here accordingly, and Professor Davis has approved the change for the purpose of this presentation.
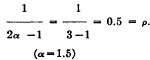
15 Political Statistics, p. 195. The distinction which Davis makes between “revolution” and “civil war” obviously is the following: a revolution is a political disturbance that is created by an underprivileged majority; a civil war is a political disturbance that is initiated by a privileged minority.
16 Ibid., pp. 195–202.
17 The distinction between real and nominal political power can be illustrated by the following examples: (1) During the Russian Revolution of 1917, nominal political power was vested in the Provisional Government; real political power resided with the Soviets. (2) During the Spanish Civil War, nominal political power could be identified with the Republican Government; real political power would have to be ascribed to the supporters of Franco. In any case, real political power is the decisive criterion; for it is the residue of real political power which enables groups to commence a revolution or a civil war.
18 An index that would measure the distribution of political power in the same manner as the concentration ratio measures the distribution of economic power, would be an additional aid. Research in that direction would be an extremely difficult, but worthwhile, undertaking.
- 6
- Cited by



Comments
No Comments have been published for this article.