Introduction
Modern humans have existed for roughly 200,000 years. They started adopting agriculture only around 12,000 years ago, and it was only around 5,000 years ago that a few populations intensified agricultural production to create economic surpluses, cities, and bureaucracies. The social Big Bang had occurred: prehistory was over, and history began, as Sumerians and Egyptians created the first two civilizations.
Archeologists and historians have long studied early civilizations, but political scientists have devoted little attention to them. This is unfortunate because political analysis can contribute a new angle to the study of civilization. A political perspective uncovers how civilizations could arise despite unfavorable odds, why civilizations arose where they did, and why they appeared coupled with another innovation: the state.
The archaeological literature, going back to Childe’s (Reference Childe1936) foundational work, emphasizes favorable endowments for food production as the driver of civilization. According to this “productivist optimism,” cities and large-scale architecture arose wherever humans could produce a substantial agricultural surplus. In turn, surpluses were most likely where settlers found a favorable array of animal and plant domesticates and where investments in water management could augment crop yields.
The problem with productivist optimism is that the endowments that made an ecology economically promising also made it geopolitically vulnerable. An alternative view, which could be called “predatory fatalism,” is based on the observation, made by historians, that taking advantage of favorable endowments could backfire. The first agricultural settlements were often surrounded by pastoralist tribes ready to loot. According to Michael Mann, “the greater the surplus generated, the more desirable it was to preying outsiders” (Reference Mann1986, 48). Indeed, “soon after cities first arose … the relatively enormous wealth that resulted from irrigation and plowing made such cities worthwhile objects of attack by armed outsiders” (McNeill Reference McNeill1992, 85). The destructive backlash was so strong that it could abort the civilization process altogether. Thucydides drew a direct link between the security backlash and a choice for economic backwardness. He viewed pre-Hellenic Greeks as “cultivating no more of their territory than the exigencies of life required, destitute of capital, never planting their land, [f]or they could not tell when an invader might not come and take it all away … consequently [they] neither built large cities nor attained any other form of greatness” (Thucydides 431BC [Warner Reference Warner1974, 35–6]).
The geographic promise of productivists suggests that given some natural advantages, humans will seize them and inevitably attain civilization. In contrast, for predatory fatalists, prosperity brings its own demise. Agricultural settlements cannot remain prosperous for long, and may choose to avoid prosperity altogether, making civilization an impossible outcome. Fatalists have not theorized why civilizations emerge. To the extent that it occurred, civilization is both a mystery and a paradox.
The contradiction in the received wisdom derives from a political blind-spot. In between the inevitabilities of geography and predation, settler societies made decisions about how to manage the tension between security and prosperity. These decisions concerned collective efforts to create major public goods for production and defense. Those decisions were eminently political, and constituted the first public choice. As a result, civilization, the successful combination of surplus production (“prosperity”) with surplus protection (“security”), was a geopolitical entity as much as an economic one.
We advance a political theory of civilization centered around the joint attainment of prosperity and security. Due to predation, in our theory civilization does not necessarily follow from the endowments emphasized by productivists. And when it occurs, it is not a miraculous escape from predation. Instead, civilization has a logic derived from the nature of the first public choice. The trade-offs facing an agricultural settlement striving for civilization were stark. On one hand, investing in irrigation could increase crop yields in the future. On the other hand, investments required sacrificing immediate consumption and the future benefits could be taken away. The decision to augment crop yields and exit subsistence agriculture was a gamble. The terms of the gamble were shaped by the initial available resources, the relative gains from investment, and the prevailing conditions of security. Geography affected all three parameters, but the decision belonged to the settlers. The analysis of such a delicate calculus is ideally suited for a formal treatment.
Our formal theory takes into account the geographic aspects emphasized by archaeologists, and the security challenges highlighted by historians. We focus on the first public choice of how to trade off growth and security to understand whether any profile of natural advantages can produce civilization in equilibrium. In our model, a “settler” (e.g., an agricultural village) receives income from a natural asset (e.g., land), and decides how to spend it across consumption, a productive investment that raises future income (yielding “prosperity”), and a defense effort for the period. A “challenger” (e.g., a pastoralist tribe) may then attack the settler to appropriate its asset and future income. If the settler spends enough on defense, the challenger may decide it is not worthwhile to attack and the settler achieves full “security.” Defense is costly however, so full security may be unaffordable and investments remain subject to a security risk. As a consequence, the settler may choose a life of subsistence rather than prosperity, forgoing civilization. The fundamentals in the settler’s decision are its initial income, the returns to investment (“growth capabilities”), and the effectiveness of defense efforts (“defense capabilities”). We investigate whether any combination of these three parameters allows for high levels of security and prosperity—our key outcome metric is a risk-adjusted measure of growth we call “civilization potential.”
We develop our theory in two parts. In the first, defense capabilities are exogenously given by nature. We show that neither high initial income nor high growth capabilities are sufficient to create civilization potential. In fact, both higher initial income and growth capabilities make the challenger more aggressive. Defense capabilities play a critical role, so the settler has its best chance at civilization when both growth and defense capabilities are high and relatively balanced. Our results rectify the view of productivists. The economic fundamentals are not the entire story, and to reach civilization a society needed to be twice-lucky in terms of growth and defense capabilities.
Were societies with low defense capabilities doomed? Some early civilizations made durable investments in protection—such as perimeter walls—that strengthened defense. In the second part of our theory, the settler can invest in defense capabilities so that defense efforts in the future become more effective at resisting attacks by the challenger. Investments in defense take time to mature, and like productive investments, they can be appropriated by the challenger. Because both kinds of investment incite immediate predation, the settler may prefer to avoid them. Indeed this is what happens if the settler’s initial income is low. However, if initial income is high enough, the settler will choose to enhance its defense capabilities to mimic the profile of a twice-lucky society and attain civilization. An intertemporal complementarity with productive investments incentivizes defense investments. If enough defense capability is built today, enhanced security will increase effective returns to productive investments tomorrow and open the path to civilization.
Integrating the productivist and the fatalist views in a formal model creates new insights. Surplus production provokes a destructive backlash that precludes civilization for societies that do not have, or cannot build, defense capabilities. Yet, an optimal first public choice offers a resolution to the paradox of civilization along two paths. One is being twice-lucky in terms of growth and defense capabilities. The other is to create artificial defense capabilities, which requires high initial income. With these predictions, we reengage the archaeological record through case studies on Sumer and Egypt, the first two civilizations.
Egypt matches the case of a twice-lucky society in our model. Growth capabilities were given by irrigation-enhanced agriculture, and defense was provided by the surrounding deserts, which protected dwellers along the Nile from most types of attack. The rise of civilization in Southern Mesopotamia could not follow the first path because the Sumerian settlements lacked natural protection and faced constant challenges from pastoral tribes. The second path to civilization in our model was open to Sumer, if it had high growth capabilities and a high initial income with which to strengthen its defenses. Both conditions are supported by archaeological scholarship. Sumerians invested heavily in water management and in protective walls, and they had an exceptional combination of initial advantages for food production. In sum, our model helps explain how civilization was possible in the first two cases on record in terms of what made them similar—high growth capabilities—and what made them different—high versus low natural defenses. The model then accounts for an associated empirical contrast: virtually all cities in Mesopotamia were surrounded by walls, while virtually none of the Egyptians were.
In the next section we review related literature and discuss broader implications of our analysis for developmental success and failure. The following section introduces our concepts of state and civilization. We then present our formal model of the first public choice. A historical section illustrates the model with case studies on Sumer and Egypt. Before concluding, we consider alternative explanations for the rise of the earliest civilizations.
Broader Implications and Related Literature
In our theory, civilization and state are conceptually different but related objects. Civilization involves attaining prosperity and achieving statehood, understood as a monopoly of violence against external threats. Our theory of civilization nests an account of pristine state formation.
Our work adds to scholarship in political science that has expanded the set of “visions of the state” beyond Tilly’s (Reference Tilly1992) account of European state formation. That expanding set considers different roots of state formation as well as other regions and times. Scholars have highlighted the role of intermediary elites in Africa (Boone Reference Boone2003) and the Middle East (Blaydes Reference Blaydes2017), the attitudes of central elites in ancient China (Tin-bor Hui Reference Tin-bor Hui2005), religious medieval practices in Europe (Grzymala-Busse Reference Grzymala-Busse2020), and coalitional dynamics in Latin America (Mazzuca Reference Mazzuca2021; Soifer Reference Soifer2015). We also shift attention away from modern Europe. Our distinctive mark is a focus on the very first states, on geographic drivers, and a compound outcome—the joint attainment of prosperity and security.
The driving forces in our theory have persisted across historical periods. Examples include ancient Chinese settlers facing raids from Mongol groups, medieval Anglo-Saxon farmers facing raids from Vikings, and Latin American port cities facing predatory caudillos in the 19th century. The dynamics of prosperity and security are also relevant to current debates about how to strengthen fragile states. Like the settler facing the challenger in our model, the fragile states of today grapple with the insecurity posed by predatory actors (World Bank 2011).
Observers have long noted that, in fragile states, foreign aid may not help recipients (Anderson Reference Anderson1999; Terry Reference Terry2002). Researchers have suggested that foreign aid can help stabilize democratic transitions (Savun and Tirone Reference Savun and Tirone2011) and diminish conflict (Savun and Tirone Reference Savun and Tirone2012). Yet, other research has suggested that aid is a curse for growth (Djankov, Montalvo, and Reynal-Querol Reference Djankov, Montalvo and Reynal-Querol2008), that it lengthens conflict (De Ree and Nillesen Reference de Ree and Nillesen2009), and that the effects of aid on governance, if positive, are only temporary (Carnegie and Marinov Reference Carnegie and Marinov2017) or context specific (Beath, Christia, and Enikolopov Reference Beath, Christia and Enikolopov2011). Findlay (Reference Findlay2018) reviews the arguments around the difficult connection between aid and peace, and Zürcher’s (Reference Zürcher2017) review of the evidence shows that aid backfires unless conditions for security are guaranteed.
Our model helps make sense of these findings by suggesting that the effects of aid are starkly conditional. In our model, aid to the settler in the form of an income windfall helps if defense and growth capabilities are high but makes conflict more virulent if defense capabilities are low. In addition, aid helps if used to develop defense capabilities alongside strong growth capabilities. The key message from our theory is that security and prosperity follow not from higher initial income but from stronger capabilities for growth and defense, and that capabilities need to be relatively balanced. We hope these observations will inform future empirical efforts on this important topic.
Institutions have long been considered important drivers of political and economic development (see, e.g., Acemoglu, Johnson, and Robinson Reference Acemoglu, Johnson and Robinson2005; Bates Reference Bates2001; Boix Reference Boix2015; North and Weingast Reference North and Weingast1989; North, Wallis, and Weingast Reference North, Wallis and Weingast2009). Our theory departs from institutionalist approaches, where legal rules constrain actors, in two directions. The first is our emphasis on the geographic roots of capacities for defense and growth. Our attention to natural endowments resonates with studies on whether natural resources pose a blessing or a curse (see, inter alia, Ross [Reference Ross2015] on the link between resources and conflict, Haber and Menaldo [Reference Haber and Menaldo2011] for the link between resources and democratization, and Jones Luong and Weinthal [Reference Jones Luong and Weinthal2006] for how the effects of resources depend on ownership structures).
Our second difference with institutionalism is our focus on coercion. We share this focus with studies of the origin of property rights (Hafer Reference Hafer2006). Yet, our object of interest is more geopolitical in nature and belongs in the vast literature on “guns and butter” analyzing conflictual relationships across groups or states (see, inter alia, Powell [Reference Powell1993] and Grossman and Kim [Reference Grossman and Kim1995] for early contributions and Garfinkel and Skaperdas [Reference Garfinkel, Skaperdas, Sandler and Hartley2007] for a review).
Much of the literature on conflict is static, but time matters in various ways. Time may allow conflict to spread (Kadera Reference Kadera1998), or it may allow for an identical conflict to be repeated (e.g., Maxwell, Reuveny, and Davis Reference Diamond2007). We consider a dynamic setting with only two actors, so conflict cannot spread, but it may reoccur, and time allows for past actions to alter the terms of subsequent conflicts—creating a dynamic linkage. A dynamic linkage is also present in models of conflict where past agreements alter the future balance of power (e.g., Fearon Reference Fearon1995; Powell Reference Powell2012). In our model, actions in one period have consequences later because investment in one period alters the resources available in the next.
We are not the first to consider a growth-defense trade-off (“guns versus butter tomorrow”) in a formal model. Kadera and Morey (Reference Kadera and Morey2008) model that trade-off. We consider a triple trade-off among investment, defense, and current consumption. To the best of our knowledge, we study the first “guns versus butter today versus butter tomorrow” problem. In addition, we derive conflict intensity as a microfounded equilibrium in a traditional model of contests and consider endogenous defense capabilities—that is, we allow for the decision maker to improve its defense technology.
Much of the work on conflict considers deterrence of outside threats through force only. Our model is no exception: the settler deters the challenger by mounting a strong enough defense.Footnote 1 This result is in line with several, long-standing, rationalist theories of deterrence reviewed by Huth (Reference Huth1999). The focus on force does abstract from other instruments of deterrence like alliances (Leeds Reference Leeds2003) or pacts (Mattes and Vonnahme Reference Mattes and Vonnahme2010). These instruments are salient in a modern, multilateral world, but were arguably less relevant during pristine state formation.
State and Civilization: A Conceptual Framework
While they co-occurred empirically, civilization and state are conceptually different. We first present our working definition of state and then how it fits into our conceptualization of civilization.
State
The canonical Weberian definition of the state as a territorial monopoly of (legitimate) violence involves two aspects: internal order (typically created through hierarchy) and external security.Footnote 2 We will consider statehood to emerge when a settlement attains significant security from external threats. Thus, we follow the canonical definition, but focus on the external dimension.
Our focus on external security contrasts with a long tradition in anthropology (referred to in the section “Other explanations”) that conceptualizes the rise of the pristine state as the emergence of an internal hierarchy that separates rulers from the rest of the population. That tradition has largely ignored the state as a source of external security. We restrict attention to the external aspect, not because we think internal hierarchy is unimportant or because our theory cannot accommodate it. Rather, the external security aspect holds the key to solving the paradox of civilization and offers a complement to theories based on hierarchy.
Civilization
The concept of civilization was first defined by archaeologists. Their definition includes surplus-producing agriculture, cities, monumental art and architecture, information recording systems (e.g., writing), organized religion, productive infrastructure (e.g., irrigation), and advances in craft production as parts of a distinct and lasting cultural identity.Footnote 3
What is relevant to our purposes is that these attributes are only possible when material production rises above subsistence levels (i.e., an economic surplus is needed). Therefore, surplus production, or “prosperity,” is an ineliminable attribute of civilization. So we agree with productivists that agricultural surplus is a basis of civilization (Childe’s Reference Childe1936 foundational insight). But surplus production cannot be the only basis for civilization.
Informed by the defense concern of fatalists, we consider that protecting surplus is as important as producing it. Surplus, and the investments that produce it, can be raided. Therefore, surplus producers must trust they will get the future rewards. In addition, security over time is crucial for civilizations to last. Therefore, surplus protection, or “security,” is the other ineliminable attribute of civilization.
Our two ineliminable attributes, surplus production via intensive agriculture and surplus protection via the state, constitute the core attributes of civilization. The other attributes remain peripheral in our conceptualization.Footnote 4 Figure 1 represents the relation between state, civilization core, and civilization overall (the list of peripheral elements is nonexhaustive).
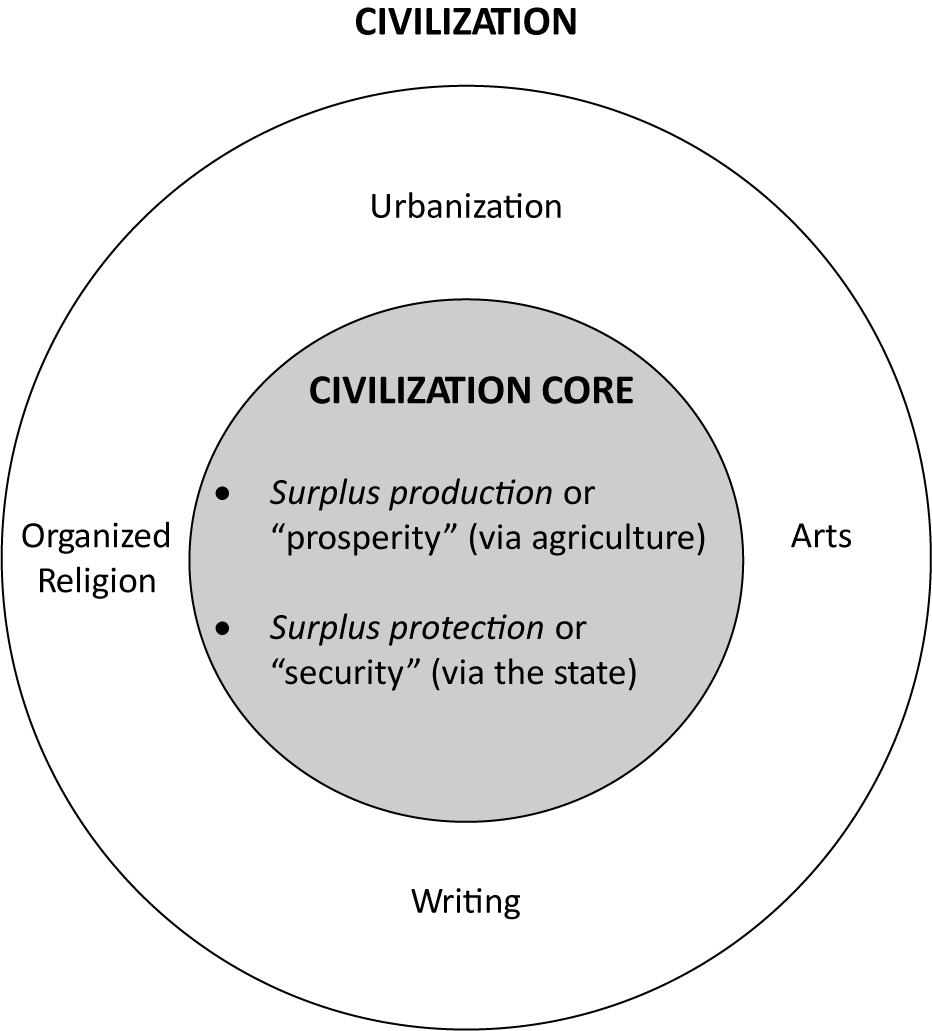
Figure 1. Conceptual Framework—State and Civilization Core
The Causal Chain of Civilization
Our stylized view of the civilization process maps geographic drivers onto prosperity and security outcomes.
We conceptualize the problem of a settlement making the first public choice to balance current consumption, future prosperity, and defense. The outcomes prosperity and security are listed in column 3 of Figure 2. The key decision fundamentals in the model are initial resources or income, and growth and defense capabilities (in column 2). These are, in turn, shaped by observable conditions of the geographic environment (in column 1) such as soil quality, topography, or sources of irrigation.
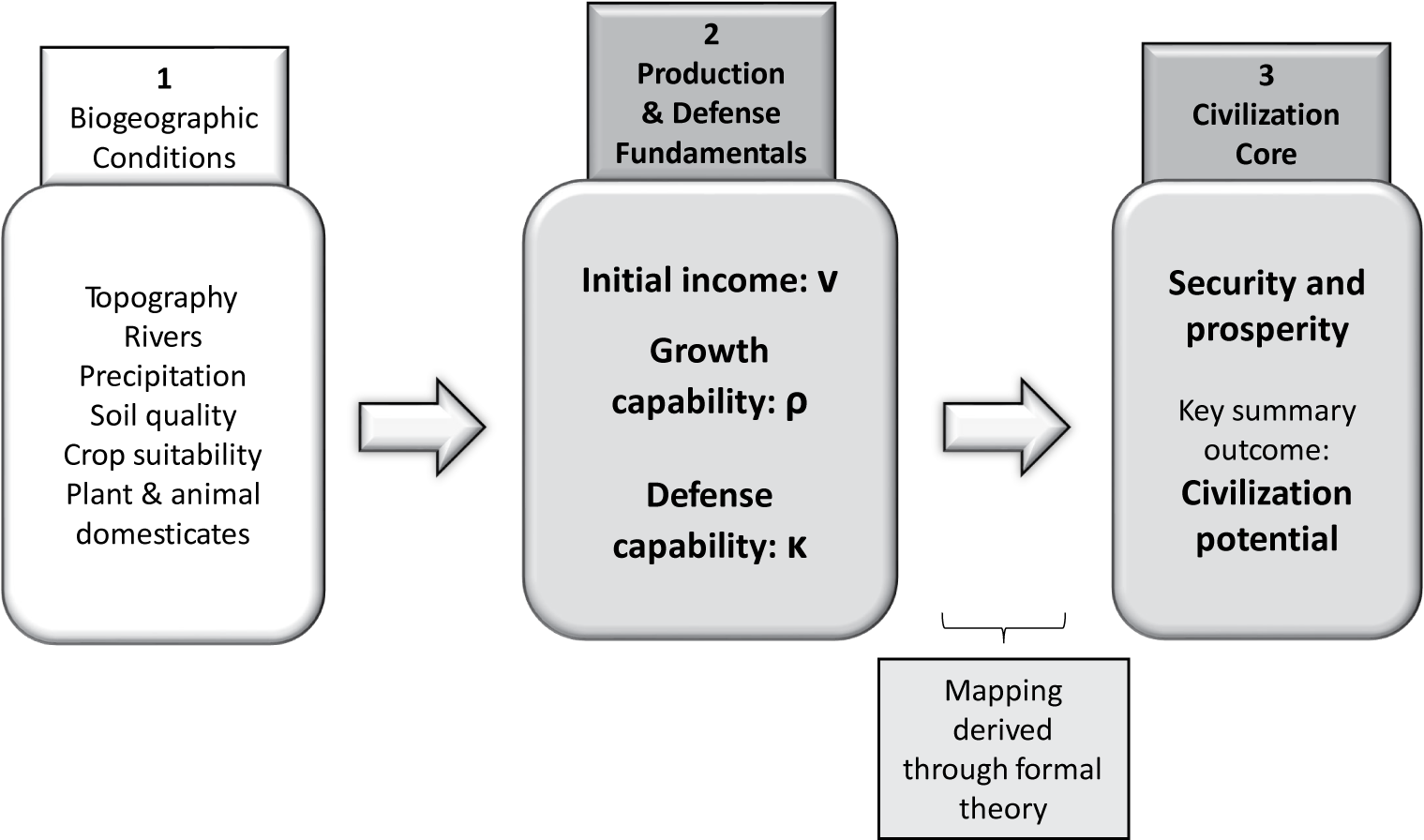
Figure 2. The Causal Chain of Civilization
The elements in columns 1 and 3 are observable. The relationship between geographic elements in column 1 and decision fundamentals in column 2 is informed by abundant scholarship in archaeology, as discussed in our case studies. Thus, theoretical statements linking fundamentals in column 2 and civilization outcomes in column 3 are testable.
The contribution of our formal theory is to show whether some combination of fundamentals in column 2 (and if so, which) can yield a sufficiently high degree of prosperity and security (outcomes in column 3). The empirical realization of civilization in the historical record surely responded not only to systematic forces but also to historical contingency and chance. To avoid a deterministic bias, the key outcome metric in the formal theory will be a score of “civilization potential.” This score combines prosperity and security through a security-adjusted measure of surplus production.
A Formal Theory of the First Public Choice
Baseline Model
Players A “settler” (it) controls a productive asset that yields an income vt > 0 in each of two periods, t = 1,2. The primary example of the asset is a tract of land. The initial income level v 1 tracks properties of the environment (e.g., climate, quality of the soil) that affect the productivity of the land and deliver an income even before the settler makes any improvements to the land. The settler faces a “challenger” (they) in each period, who wants to seize the asset to get its income in the next period. Our settler represents the historical role of agricultural producers that gave rise to the first cities. Our challenger represents the predatory groups, typically nomadic pastoralists, who raided agricultural settlements. Our assumption that each actor is unipersonal makes clear that we abstract from internal social hierarchy.Footnote 5
Actions, resources, technology In each period t, the settler can spend vt across productive investment or defense, consuming any remainder. A productive investment of it units of income adds ρit units to the future yield of the asset, so income in t + 1 is v
t+1 = vt + ρit. The parameter
$ \rho $
captures factors that affect the returns to productive investment, such as the additional crop yields attained by investing in water management. We assume
$ \rho $
> 1, which makes investment possible although not inevitable due to insecurity.Footnote
6 For simplicity, we abstract from depreciation and discounting.
In each period t, the settler can put together a defense dt, which costs the amount
$ \frac{d_t}{\kappa_t} $
, where κt ≥ 0 is the settler’s defense capability. The higher the defense capability of the settler, the higher the “firepower”
$ {d}_t $
attained by a given expense
$ \frac{d_t}{\kappa_t} $
. The parameter
$ {\kappa}_t $
captures the technology of defense—that is, any elements that affect the cost of transforming resources into protection. For instance, if the settler can place soldiers behind a desert or on top of elevated terrain that wears down the approaching challenger, then the settler will be able to mount a stronger defense. We fix κt = κ
1 > 0 in our baseline analysis (e.g., κt is given by natural terrain). In the subsection “Extended Model: Another Path to Civilization,” we allow κt to be improvable (e.g., κt can be enhanced with fortifications).
The challenger can attack the settler with an intensity at ≥ 0. If at = 0, there is peace. If at > 0, conflict occurs at the end of period t. The winner in t will own the asset, and the income it generates, in t + 1.Footnote
7 We adopt the typical Tullock contest success function, so whenever the challenger attacks, the settler prevails with probability
$ P\left( settler\ wins\right)\equiv \frac{d_t}{d_t+{a}_t} $
and the challenger wins with the complementary probability.Footnote
8 If the challenger does not attack, the settler has successfully deterred the challenger, and this lack of challenge results in full security (P(settler wins) = 1).
Timing At the beginning of each period, the settler chooses defense dt and investment it, consuming any remaining resources. After observing (dt,it) the challenger selects their attack at. The winner (the settler, if there is peace) moves to the next period (if any) in control of the asset.
Payoffs Both settler and challenger are risk neutral and care linearly about consumption in each period. The settler while in control of the asset consumes
$ {c}_t\equiv {v}_t-\frac{d_t}{\kappa_t}-{i}_t $
in period t. Thus, in any period t the settler chooses dt and it to maximize the value of being in control of the asset, which is the value of expected intertemporal consumption
$ {V}_t={v}_t-\frac{d_t}{\kappa_t}-{i}_t+\frac{d_t}{d_t+{a}_t}{V}_{t+1} $
, while observing the budget constraint (BC)
$ {v}_t-\frac{d_t}{\kappa_t}-{i}_t\hskip0.3em \ge \hskip0.3em 0 $
. The initial settler’s value is
$ {V}_1={c}_1+\frac{d_t}{d_t+{a}_t}{c}_2 $
. The challenger only cares about the value of being in control of the asset, and in period t chooses at to maximize the value of attacking the settler net of costs
$ \frac{a_t}{d_t+{a}_t}{V}_{t+1}-{a}_t $
. If the challenger does not attack or is defeated, their payoff is zero. Table 1 summarizes the notation of our baseline model.
Table 1. Baseline Model: Summary of Notation
Our focus is on whether the settler invests and is likely to enjoy the returns of investment. Growth does not benefit the settler if the challenger wins. Our definition of civilization as a combination of prosperity and security is operationalized through a security-adjusted measure of growth, our measure of civilization potential
$ CP $
$ =P\left( settler\ wins\right)\times $
$ \left({v}_2^{\ast }-{v}_1\right) $
$ =\frac{d_1^{\ast }}{d_1^{\ast }+{a}_1^{\ast }}\rho {i}_1^{\ast } $
(asterisks indicate equilibrium magnitudes). In words, this is the product of the probability that the settler prevails in equilibrium, or security, times the surplus created by investment, or prosperity. The remainder of this section investigates whether any combination of parameter values v
1, κ
1, and
$ \rho $
gives the settler a positive civilization potential.
Solution concept We solve for a subgame perfect Nash equilibrium by backward induction, starting with the second period, and then studying the first.
Modeling choices and robustness
Our goal is to formalize the first public choice for an agricultural settlement that is striving to achieve civilization. This motivates placing the settler as a key player in our model, facing the attacks of pastoralist groups.
We have only introduced asymmetries between the players that we deem helpful to analyze the trade-offs of interest. Allowing only the settler to invest maintains tractability and matches historical situations where one settled, food-producing group has more room to accumulate than do rival nomadic groups.Footnote 9 Letting the settler move first helps make deterrence possible, an important outcome in our analysis. Last, while defense effort burns limited resources for the settler, attack effort does not deplete a budget for the challenger. This avoids the technical difficulties involving a kink in the challenger’s best response function that would make the analysis less elegant without gaining insight.
The presence of an initial income parameter v
1 is uncontroversial, but the introduction of our two capabilities requires justification. One fundamental trade-off facing the settler involves whether to sacrifice current consumption to make investments that will increase crop yields. That motivates the inclusion of returns on investment
$ \rho $
. However, the trade-off between consuming now and later is affected by insecurity, which creates a second trade-off. The risk, according to the fatalist view, is the possibility of predation, which motivates including the challenger, as well as the possibility of conflict. The parameter ĸ
1 sets the rate at which income can be turned into defense. The two capabilities (κ
1,
$ \rho $
) govern the central trade-offs in the theory.
Our model is robust to a number of extensions available upon request. These include considering more than two periods, populations who choose whether to adopt the role of settlers and challengers, the possibility of transfers between the settler and the challenger, and destruction from conflict.
Solution
Second period Success in conflict pays off one period later, so the challenger does not attack in the second and last period, leaving
$ {a}_2^{\ast }=0 $
. Anticipating this, the settler chooses zero defense expenditures, leaving
$ {d}_2^{\ast }=0 $
. The proceeds from productive investment only materialize in the future, so the settler does not invest in the last period, leaving
$ {i}_2^{\ast }=0 $
. Since neither conflict nor investment will occur in t = 2, the value of keeping the asset is the income that the asset will yield then (i.e.,
$ {V}_2={v}_2\equiv {v}_1+\rho {i}_1 $
), which will be consumed in its entirety (the winner in period 1 will consume c
2 = v
2 in period 2). This captures why the settler might want to invest in t = 1: investment grows future income and, conditional on remaining in control, higher future income yields higher future consumption.
First period After the settler makes its defense and investment choices (d
1,i
1), the challenger chooses the attack intensity a
1 to maximize
$ \frac{a_1}{d_1+{a}_1}{v}_2-{a}_1 $
. The first order condition for the challenger is
$ \frac{d_1}{{\left({d}_1+{a}_1\right)}^2}{v}_2=1 $
. The second derivative of the challenger’s objective function is strictly negative for all a
1, so the optimal attack intensity by the challenger is
$ {a}_1\left({d}_1,{v}_2\right)=\sqrt{d_1{v}_2}-{d}_1 $
if
$ \hskip0.1em {d}_1<{v}_2 $
and zero otherwise.
The challenger’s optimal attack function a
1(d
1,v
2) contributes to the key trade-off facing the settler. Since ρ > 1, investment increases future income, v
2 = v
1 + ρi
1, but lowers the chance that the settler can keep that income as a more valuable asset makes the challenger more aggressive (formally,
$ \frac{\partial {a}_1\left({d}_1,{v}_2\right)}{\partial {i}_1}=\frac{\rho }{2}\sqrt{\frac{d_1}{v_2}}>0 $
whenever d
1 < v
2). This originates the civilizational paradox: attempting future prosperity raises insecurity, which in turn depresses incentives to attempt that prosperity.Footnote
10
The challenger’s attack function a 1(d 1,v 2) also shows that attack intensity becomes zero if the settler raises defense to v 2 or higher. Such full deterrence makes the settler completely secure. Because defense is costly, the settler will never choose a defense higher than the minimum needed to achieve deterrence, implying the optimizing settler will observe a deterrence constraint (DC) d 1 < v 2.
The settler maximizes its expected intertemporal consumption value V 1 subject to the budget constraint (BC) and the deterrence constraint (DC). The settler’s problem in period 1 can then be written as
$$ \underset{d_1,{i}_1}{\max}\left\{{v}_1-\frac{d_1}{\kappa_1}-\hskip0.2em {i}_1+\frac{d_1}{d_1+{a}_1\left({d}_1,{v}_1+\rho {i}_1\right)}\left({v}_1+\rho {i}_1\right)\right\}, $$
subject to
$$ {v}_1-\frac{d_1}{\kappa_1}-{i}_1\hskip0.3em \ge \hskip0.3em 0\hskip0.2em (BC) $$
$$ {v}_1+\rho {i}_1-{d}_1\hskip0.3em \ge \hskip0.3em 0\hskip0.2em (DC) $$
$$ {d}_1\hskip0.3em \ge \hskip0.3em 0 $$
$$ {i}_1\hskip0.3em \ge \hskip0.3em 0. $$
The settler’s objective in equation (1) reflects the fact that defense and investment in t = 1 are costly in terms of current consumption (the second and third terms
$ -\frac{d_1}{\kappa_1}-{i}_1 $
). However, investment i
1 yields returns ρi
1 in the future, and defense raises security, or the probability
$ \frac{d_1}{d_1+{a}_1(.)} $
that the settler keeps its income in period 2. The objective also reflects the gamble of attempting prosperity. The settler is not guaranteed the full return ρi
1 to its investment but only the risk-adjusted return
$ \frac{d_1}{d_1+{a}_1(.)}\rho {i}_1 $
once security is factored in.
We characterize the solution
$ \left({d}_1^{\ast },{i}_1^{\ast },{\lambda}_{BC}^{\ast}\right) $
to the settler’s problem for each parameter combination
$ \left({\kappa}_1,\rho, {v}_1\right)\hskip0.4em \in \hskip0.4em {\mathrm{\mathbb{R}}}_{+}\times \left(1,\infty \right)\times {\mathrm{\mathbb{R}}}_{+}. $
In other words, we establish whether and how much the settler defends itself, invests, and consumes (and, in turn, whether it attains any civilization potential), for each possible combination of the parameter values. Finding the solution is tedious but involves only standard Kuhn–Tucker optimization techniques. The Lagrangian for the settler’s optimization is
$$ {\displaystyle \begin{array}{l}\mathcal{L}={v}_1-\frac{d_1}{\kappa_1}-{i}_1+\frac{d_1}{d_1+{a}_1\left({d}_1,{v}_1+\rho {i}_1\right)}\left({v}_1+\rho {i}_1\right)\\ {}\hskip1.2em +{\lambda}_{BC}\left({v}_1-\frac{d_1}{\kappa_1}-{i}_1\right)+{\lambda}_{DC}\left({v}_1+\rho {i}_1-{d}_1\right)+{\lambda}_d{d}_1+{\lambda}_i{i}_1,\end{array}} $$
where
$ {\lambda}_{BC} $
,
$ {\lambda}_{DC} $
,
$ {\lambda}_d $
, and
$ {\lambda}_i $
are the Lagrange multipliers for each constraint described in Equation 2 – Equation 5. The first order and complementary slackness (c.s.) conditions that characterize the optimum are given by
$$ {\displaystyle \begin{array}{c}\frac{\partial \mathcal{L}}{\partial {d}_1}=\frac{1}{2}\sqrt{\frac{v_1+\rho {i}_1}{d_1}}\hskip0.4em -\hskip0.2em \frac{1}{\kappa_1}\hskip0.2em -\hskip0.2em \frac{\lambda_{BC}}{\kappa_1}\hskip0.2em -\hskip0.2em {\lambda}_{DC}+{\lambda}_d\\ {}\hskip-0.2em =0;{d}_1\hskip0.3em \ge \hskip0.3em 0,{\lambda}_d\hskip0.3em \ge \hskip0.3em 0,{\lambda}_d{d}_1=0\hskip0.6em \mathrm{c}.\mathrm{s}.\end{array}} $$
$$ {\displaystyle \begin{array}{c}\frac{\partial \mathcal{L}}{\partial {i}_1}=\frac{\rho }{2}\sqrt{\frac{d_1}{v_1+\rho {i}_1}}\hskip0.4em -\hskip0.2em 1\hskip0.2em -\hskip0.2em {\lambda}_{BC}+{\lambda}_{DC}\rho +{\lambda}_i\\ {}\hskip-1.1em =0;{i}_1\hskip0.3em \ge \hskip0.3em 0,{\lambda}_i\hskip0.3em \ge \hskip0.3em 0,{\lambda}_i{i}_1=0\hskip0.4em \mathrm{c}.\mathrm{s}.\end{array}} $$
$$ {\lambda}_{BC}\left({v}_1-\frac{d_1}{\kappa_1}-\hskip0.2em {i}_1\right)=0\hskip0.4em \mathrm{c}.\mathrm{s}.,{\lambda}_{DC}\left({v}_1-\hskip0.2em {d}_1+\rho {i}_1\right)=0\hskip0.4em \mathrm{c}.\mathrm{s}. $$
The conditions of equations (7)–(9) are necessary and sufficient for a maximum because the constraints are linear and the objective is smooth and concave in the control variables d 1 and i 1. The Appendix offers technical details on the solution.
To build intuition before we describe the equilibrium, suppose the settler chooses arbitrary investment and defense expenses
$ {i}^o $
and
$ {d}^o $
, respectively. These expenditures buy respectively
$ {i}_1={i}^o $
units of investment and
$ {d}_1={d}^o{\kappa}_1 $
units of defense. Now consider changes to the parameters
$ \rho $
and κ
1. An increase in
$ \rho $
raises future income
$ {v}_2={v}_1+\rho {i}^o $
at the rate
$ {i}^o $
, but this new prosperity makes the challenger more aggressive, increasing insecurity. An increase in κ
1 raises the settler’s defense at the rate
$ {d}^o $
, and even after accounting for the challenger’s adjustment of their attack, it increases security (using the challenger’s attack function
$ {a}_1\left({d}_1,{v}_2\right)=\sqrt{d_1{v}_2}-{d}_1, $
the probability that the settler prevails is
$ \frac{d_1}{d_1+{a}_1\left({d}_1,{v}_2\right)}=\sqrt{\frac{d^o{\kappa}_1}{v_2}} $
, which increases in κ
1). These direct effects of the parameters, before we allow the settler to adjust its choices, are described in Panel (a) of Figure 3, and they represent the critical forces shaping the optimal choice by the settler. The settler may respond to very low investment returns by not investing at all, forgoing any civilization potential. In turn, the settler may find that higher returns bring about so much insecurity that even then investing is ill-advised. Yet, the risk may be acceptable if defense capabilities are high enough for a small expenditure on defense to buy a lot of security. The next proposition elucidates whether and when the settler can buy enough security that it makes sense to attempt prosperity.
Proposition 1 In a world with exogenous defense capabilities,
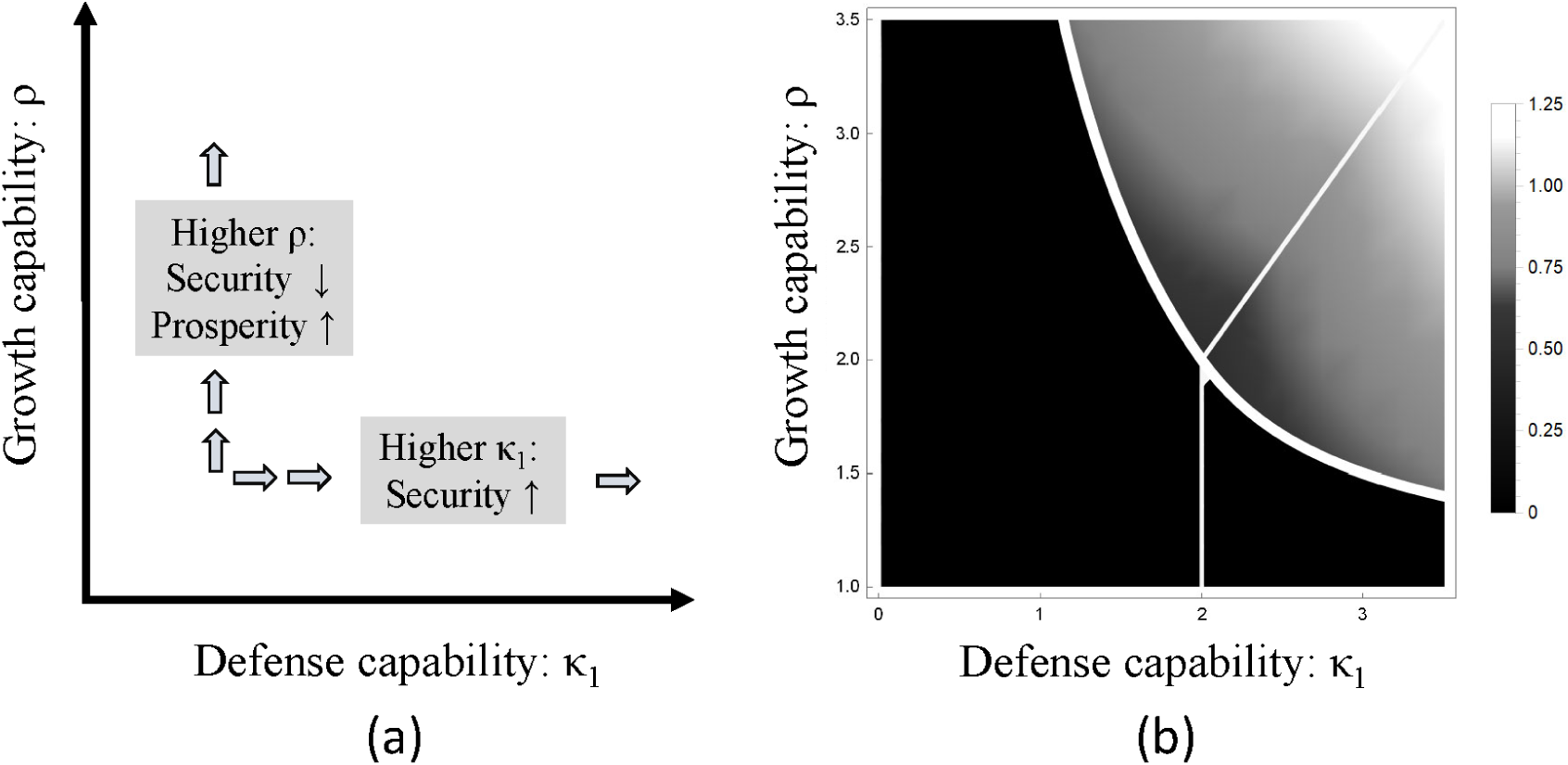
Figure 3. Growth and Defense Capabilities Shape Civilization Potential
Panel (a): Direct effects holding settler actions fixed. Panel (b): Lighter shading represents higher Civilization Potential (computed in equilibrium assuming v1 = 1).
(i) If defense and growth capabilities (κ
1,
$ \rho $
) are both sufficiently high, prosperity arises with partial or full security and higher capabilities increase civilization potential. If either defense or growth capabilities are low, civilization potential remains zero.
(ii) No level of initial income v1—no matter how high—can produce civilization when defense or growth capabilities are low. High levels of initial income increase civilization potential only when both defense and growth capabilities are sufficiently high.
Panel (b) of Figure 3 illustrates the properties of the solution in terms of civilization potential. In a safe environment without a challenger, the settler would invest—and prosperity would arise—everywhere in the quadrant (κ
1,
$ \rho $
). In the presence of the challenger, however, prosperity remains beyond reach for a portion of the parameter space (κ
1,
$ \rho $
). In the dark area to the left and below the thick white convex curve, civilization potential
$ CP=\frac{d_1^{\ast }}{d_1^{\ast }+{a}_1^{\ast }}\rho {i}_1^{\ast } $
remains zero because insecurity discourages investment completely. As per the fatalists, insecurity can indeed preclude civilization. In that dark area, defense capabilities are too low to mitigate security risks, and investment is forgone; conversely, growth capabilities are too low to make investment attractive given the security risk. Throughout, we will refer to capabilities being “low” to indicate the pairs (κ
1,
$ \rho $
) below and to the left of the convex curve, that yield no civilization potential (“high” capabilities are those above the curve).
Against the fatalists, however, civilization is possible. In the areas above the convex curve civilization potential becomes positive, and as the pairs (κ
1,
$ \rho $
) move toward the northeast of the quadrant civilization potential increases (lighter shading in the graph indicates higher values of civilization potential; shading in the graph tracks equilibrium civilization potential assuming v
1 = 1). Because high growth and defense capabilities yield high civilization potential, we consider that combination of fundamentals the predictor of empirically realized civilization.
The position of the convex curve in Panel (b) of Figure 3 is independent of initial income. More income raises civilization potential wherever this potential is positive (above the curve) but does not help if capabilities hold civilization potential at zero (below the curve). This is a surprising result. The intuition is as follows. A higher income allows the settler to buy more defense but also makes the challenger more aggressive. Holding growth capabilities fixed, when defense capabilities are high the settler can buy defense cheaply. Then a higher income helps the settler increase defense fast enough relative to external aggression, so the higher income raises the risk-adjusted returns for an investing settler and raises civilization potential. Below the convex curve, defense capabilities are too low, so if income increases, defense cannot rise fast enough to protect investment, and therefore no amount of income can produce civilization.
The solution to the settler’s problem has three substantive implications. First, taken together, parts (i) and (ii) of proposition 1 imply that what is crucial to create civilization is capabilities, not initial income. Archaeologists emphasize favorable conditions for food production but conflate initial advantages (e.g., rivers offer fish) and the potential for investments (e.g., rivers support infrastructure for water management). The latter aspect, our model shows, is critical.
Second, the exclusive focus on the geography of food production is misleading. Civilization potential can be zero in our model despite a high initial income, or a high return to investment. Security matters, and so do defense capabilities. The third substantive implication is that a broadly balanced profile of capabilities is helpful to civilization. The curve separating the areas with and without civilization potential is strictly convex to the origin and does not intersect the axes, so it does not pay the settler to have 100% of its capabilities concentrated on one axis (either κ
1 or
$ \rho $
). Equal amounts of both capabilities will be more likely to land the settler in the area with positive civilization potential.
In sum, the first key takeaway from the analysis is that the paradox of civilization has a solution. This is a necessary analytical outcome to explain how civilization was possible. The second takeaway is a rectification of the production optimism of archaeologists. Since the civilization core is surplus production and also surplus protection, achieving it requires the settler to be twice-lucky by having high growth and defense capabilities.
Additional remarks The model produces varieties of civilizational success and failure. Both the areas with and without civilization potential include subcases, so not all failures and successes are created equal. The subcases within each area are separated by the thin white lines in Panel (b) of Figure 3. The dark area without civilization potential has a subregion to the right of the value κ 1 = 2 where the settler attains deterrence by forgoing prosperity, echoing Thucydides’s observation. In the subregion to the left of κ 1 = 2, the settler is insecure despite forgoing prosperity—a stagnation-conflict trap. The area with positive civilization potential also shows variation. In the subregion above the 45 degree line, the settler invests despite being unable to fully deter the challenger (the security risk is not so high as to deter all investment), and in the subregion below the 45 degree line the settler both prospers and fully deters the challenger. High levels of civilization potential can be reached with varying combinations of prosperity and security.
These results can inform policy toward contemporary failed states where central authorities are powerless to deter violent predatory actors. In our model, these states are close to the origin in the (κ
1,
$ \rho $
) space, the stagnation-conflict trap where insecurity is high and productive investments are discouraged. Part (ii) of our proposition implies that no income windfall from outside aid will help the society avoid conflict or grow. Part (i) of the proposition implies that changes in capabilities are needed, and that a relatively balanced increase in both capabilities is the best path to security and prosperity.
Extended Model: Another Path to Civilization
In our baseline model, even a settler with high growth capability ρ cannot attain civilization if its initial defense capability κ 1 is too low. But some societies succeeded despite initial insecurity. In fact, the mark of many civilizations were defensive structures built to overcome insecurity. We now extend the model to allow for the endogenous strengthening of defense capabilities and ask whether a settler with low initial defenses can attain civilization.
Setup
In each period, a challenger arrives who seeks to replace the settler and inherit its capabilities. Like in our baseline model, in each period the settler chooses productive investment it and defense dt, but now the settler can also spend resources mt in one period to increase its defense capability in the next, to
$ {\kappa}_{t+1}={\kappa}_t+{m}_t $
. The settler’s budget constraint in period t becomes
$ {v}_t-\frac{d_t}{\kappa_t}-{i}_t-{m}_t\hskip0.3em \ge \hskip0.3em 0 $
.Footnote
11
Now we need to consider three periods, 0, 1, and 2. Since the challenger will never fight in period 2, the settler will never spend to expand defense capability in periods 1 or 2; thus, the decision to expand defense capability is only relevant in period 0. In terms of Figure 3, choosing m
0 > 0 in period 0 to increase defense capabilities in period 1 moves the settler horizontally to the right in the space (κ
1,
$ \rho $
). After observing the settler’s choices (m
0,dt,it), the challenger selects its attack intensity at. If at = 0, the settler retains its position in the next period. If at > 0, then war occurs in period t. The winner becomes the settler in the next period (if any), and faces a new challenger then.
Effectively, in this expanded model the settler in t = 0 chooses what version of the game in our previous subsection to play by varying κ 1. The advantage of a higher κ 1 is that it could shift the settler from a situation without civilization potential to one with positive civilization potential. The disadvantage is twofold. First, expanding defense capability reduces consumption in t = 0. Second, since defense capabilities can be inherited by a successful challenger who defeats the settler at t = 0, investments in defense capabilities encourage attacks before those investments mature (just like productive investments).
The case of interest is one where the settler needs to overcome defenselessness. So we consider a settler that in the absence of improvements in defense capability would find itself under attack and making no productive investments in t = 1.
Solution
As before, we solve the model through backward induction. Actions in periods 1 and 2 follow the logic in our baseline model. Given the initial parameters (v
0,κ
0,
$ \rho $
), the choices (i
0,m
0) of the settler in t = 0 position the settler into the game of our baseline model with capabilities (κ
1,
$ \rho $
). Investments m
0 in defense capabilities increase security in t = 1 and therefore increase the settler’s payoff starting in period 1, provided that the settler survives conflict in period 0. Once in period 1, the settler has a continuation value of
$ {V}_1\left({i}_0,{m}_0\right)=\left({v}_0+\rho {i}_0\right)\times S\left({m}_0\right) $
, where the function
$ S\left({m}_0\right) $
(detailed in the Appendix) captures how payoffs in t = 1 change with m
0. Given the continuation value
$ {V}_1\left({i}_0,{m}_0\right) $
, we can solve for decisions in period 0.
After the settler has selected m
0, d
0, and i
0, the challenger decides whether to fight. Using the same logic as in the baseline model, the challenger’s attack function is
$ {a}_0\left({d}_0,{i}_0,{m}_0\right)=\sqrt{d_0{V}_1\left({i}_0,{m}_0\right)}-{d}_0 $
if
$ {d}_0<{V}_1\left({i}_0,{m}_0\right) $
and zero otherwise. The value
$ {V}_1\left({i}_0,{m}_0\right) $
of being in control of the asset in t = 1 is increasing in both productive (i
0) and defensive (m
0) investments, so both kinds of investment incentivize challenge in t = 0.
Given the challenger’s best response function, the settler chooses d 0,i 0, and m 0 to maximize its expected value V 0. The settler’s optimization problem is
$$ \underset{d_0,{i}_0,{m}_0\hskip0.3em \ge \hskip0.3em 0}{\max }{v}_0-{m}_0-\frac{d_0}{\kappa_0}-{i}_0+\frac{d_0}{d_0+{a}_0\left({d}_0,{V}_1\left({i}_0,{m}_0\right)\right)}{V}_1\left({i}_0,{m}_0\right), $$
subject to the nonnegativity constraints
$ {d}_0\hskip0.3em \ge \hskip0.3em 0,{i}_0\hskip0.3em \ge \hskip0.3em 0,{m}_0\hskip0.3em \ge \hskip0.3em 0 $
, the budget constraint
$ {v}_0-{m}_0-\frac{d_0}{\kappa_0}-{i}_0\hskip0.3em \ge \hskip0.3em 0, $
and the deterrence constraint
$ \left({v}_0+\rho {i}_0\right)S\left({m}_0\right)-{d}_0\hskip0.3em \ge \hskip0.3em 0 $
.
We now establish,
Proposition 2
Given unfavorable initial defense capabilities κ0, if initial income v
0 is low enough, then no investments in defense capabilities are made and civilization potential remains zero. However, a high enough initial income v
0 yields a positive civilization potential. Specifically, defense investments are made in t = 0 to increase defense capabilities κ1 in t = 1; the increased defense capabilities in t = 1 make productive investments i
1 secure, making civilization potential positive. This civilization potential, in turn, increases with growth capabilities
$ \rho $
.
This proposition says that when initial income v 0 is low, it is preferable to consume in the present rather than augment predatory risk by making any kind of investments. A little initial income does not translate into a little investment in defense capabilities because improvements in defense capabilities also incite immediate predation and only become protective in the following period. A “critical mass” of income is needed. When v 0 is high enough, two advantages materialize. First, the settler can finance a higher defense effort while it waits for defense investments to mature. Second, a critically large investment in defense capability is possible at t = 0; as a consequence, the additional security in t = 1 is large enough to make the effective rate of return in t = 1 attractive for productive investment. The result is prosperity in t = 2. That expected prosperity justifies bearing the initial costs and risks associated with investments in defense. The force at play is an intertemporal complementarity between defense and productive investments. Stronger defense capabilities make possible a positive civilization potential, and this civilization potential is higher when growth capabilities are high.
We have derived two propositions that connect parameter values and civilization potential. The predictions differ from the blunter observation that a high value of every parameter is good for civilization. The key point is that high initial income and growth capabilities are not individually sufficient for civilization.Footnote 12 Instead, high growth capabilities must be paired either with high natural defenses or a high initial income to build artificial defenses. In other words, there are two broad paths to civilization, represented schematically in Figure 4. When both growth and defense capabilities are high, civilization potential arises as in our baseline model. When natural defense capabilities are low, a high income can finance artificial ones.
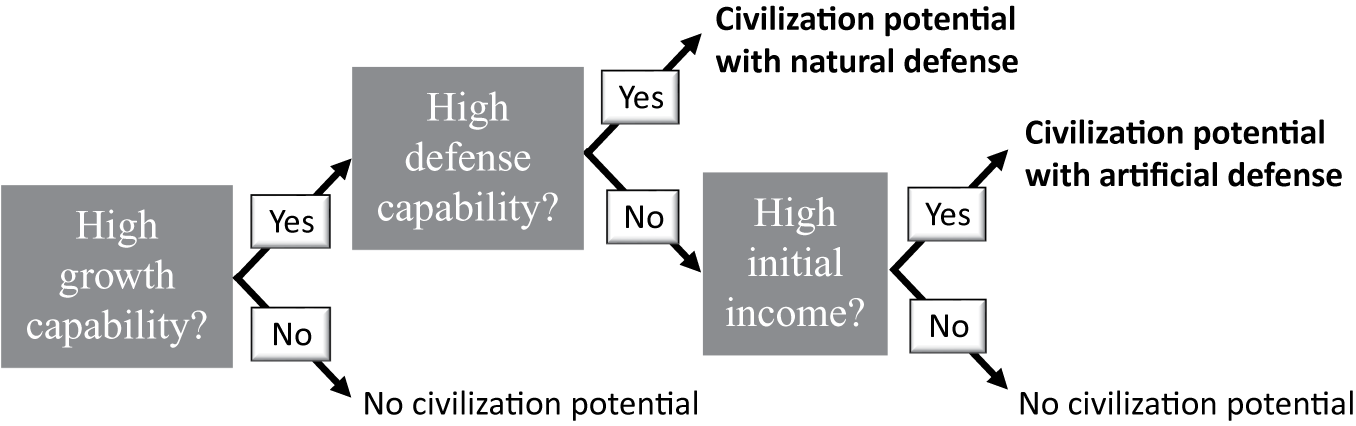
Figure 4. Paths to Civilization
The requirements for the second path to civilization—high growth capability and high income—may seem close to the conditions highlighted by productivists. However, our results make clear that initial income and growth capabilities each play a different role in the civilization process. Income matters in the second path because it finances defense infrastructure, a mechanism beyond the scope of conflict-free productivism.
Historical Illustrations: Sumer and Egypt
Sumer and Egypt are the most prominent pristine civilizations. Sumer, located in Southern Mesopotamia, supported the first substantial surpluses in human evolution, the first city-states, and gave rise to the first major civilization. Egypt was the first society to attain security and prosperity on a large scale—temporally and territorially.
The case studies in this section make two contributions. First, they help assess our assumptions—that is, whether the theory captures the main challenges and opportunities facing the first civilizations. Second, the cases illustrate the theoretical results on what it takes to escape the paradox of civilization. Each historical case matches one of the two paths to civilization identified by our theory.
Shared Growth Capabilities and Similar Investments in Productive Infrastructure
Sumer was located in a riverine valley, along the Tigris and Euphrates, exceptionally endowed for alluvial agriculture. The alluvium greatly expanded soil fertility. But to make the best use of the alluvium, Sumerians made massive investments in irrigation infrastructure, securing extraordinary returns. According to Mann (Reference Mann1986, 78), “If [the alluvium] can be diverted onto a broad area of existing land, then much higher crop yields can be expected… . Rain-watered soils gave lower yields.” The spreading of alluvial flows required investments in canals, and these investments repaid the efforts. Liverani (Reference Liverani and Snell2008, 5) gives an idea of the increase in yields: “The agricultural production of barley underwent a notable, possibly tenfold, increase thanks to the construction of water reservoirs and irrigation canals.”
Like Sumerians, Egyptians could vastly increase their economic output by investing in water management, which in the Nile valley took the form of basin irrigation. Egyptians used a grid of basins to trap the floodwater and increase soil fertility.Footnote
13 Scholars agree that in Egypt irrigation agriculture “could generate crop-to-seed yields of between 12:1 and 24:1 … but only at the cost of high capital investments” (Morris and Manning Reference Morris, Manning, Smelser and Swedberg2005, 141). For Mann, both in Egypt and Mesopotamia, irrigation agriculture could “generate a surplus far greater than that known to populations on rain-watered soil” (Reference Mann1986, 80). The consensus is that investments in irrigation created the earliest forms of systematic surplus. The high returns to investments in irrigation infrastructure for both Egypt and Sumer correspond to a high value of the growth capability
$ \rho $
in our model.
Different Defense Capabilities and Different Investments in Defense Infrastructure
Historians have remarked that territorial isolation protected settlers along the Nile from enemies. According to Bradford (Reference Bradford2001, 9), “The sea to the North and the deserts West and East isolated the Egyptians from the rest of mankind, except for merchants, some infiltrators, and the occasional raid.” The sea acted as a shield during the formative period of Egyptian civilization. Yet, the largest and most durable protection for Egyptians was afforded by the deserts surrounding the Nile basin. The desert made invasions much less likely than in other food-producing centers for two reasons. It discouraged the emergence and settlement of hostile neighbors nearby and acted as a barrier against more distant rivals. In terms of our model, Egypt’s territorial isolation maps into a naturally high κ 1. Although the desert had no economic value, it was a key security asset.
As a result, Egypt matches the description of a twice-lucky location, boasting high growth and defense capabilities, and exemplifies locations to the northeast area of Figure 3, which are predicted by our baseline model as having a high civilization potential.
In contrast to Egypt, Sumer was exposed to numerous threats. As Bradford (Reference Bradford2001, 4) puts it, “Their neighbors to the West … infiltrated Mesopotamia… . The neighbors to the East, who dwelled in the mountains, were the Gutians and the Elamites. The Gutians and, to a lesser extent, the Elamites considered Sumer and Akkad a treasurehouse to be raided.” Sumer was located in a plain “ringed to North and East by mountains, the millennial home of barbarous highlanders, always ready and eager to descend on the wealthy cities below” (Finer Reference Finer1997, Book I, 105). In terms of our model, the vulnerability of Sumerian settlements to invaders means that natural defense capability was lower than in Egypt.
But if output was insecure in Sumer, how could the first human civilization emerge? Our model with endogenous defense capabilities provides an answer. According to Proposition 2, the key requirement was for Sumerians to have a high initial income v 0 they could use to build the defense capabilities nature did not provide. This would raise their defense capability κ 0 to a higher level κ 1 that would shift Sumer from a part of the parametric space without civilization potential to a part with high potential, thus mimicking the Egyptian profile of capabilities. We illustrate such a shift in Figure 5.
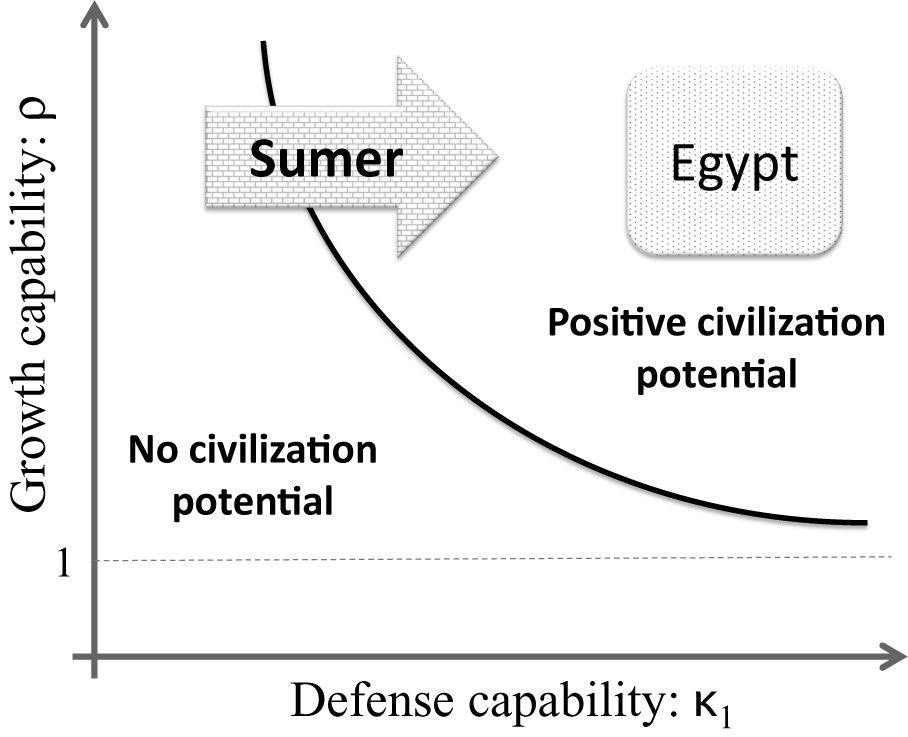
Figure 5. Historical Realization of the Two Paths to Civilization
Two pieces of evidence must be present for the Sumerian case to match our theory. There must be archaeological evidence of investments to improve defense and of a high initial income that could fund those investments.
Indeed, the archaeological record offers evidence of important investments to improve security. Ditches, moats, and perimeter walls emerged with the first settled groups, and grew in complexity over time, to make Sumerian cities large-scale fortifications. Perimeter walls are prominent in maps of Sumerian cities (Figure 6 illustrates). Virtually all ancient cities in Mesopotamia and the Levant—Jericho being a famous early example—had walls.Footnote 14 Walls were the endogenous, artificial substitute for the missing natural protection that was present in Egypt (where typical cities did not have walls).
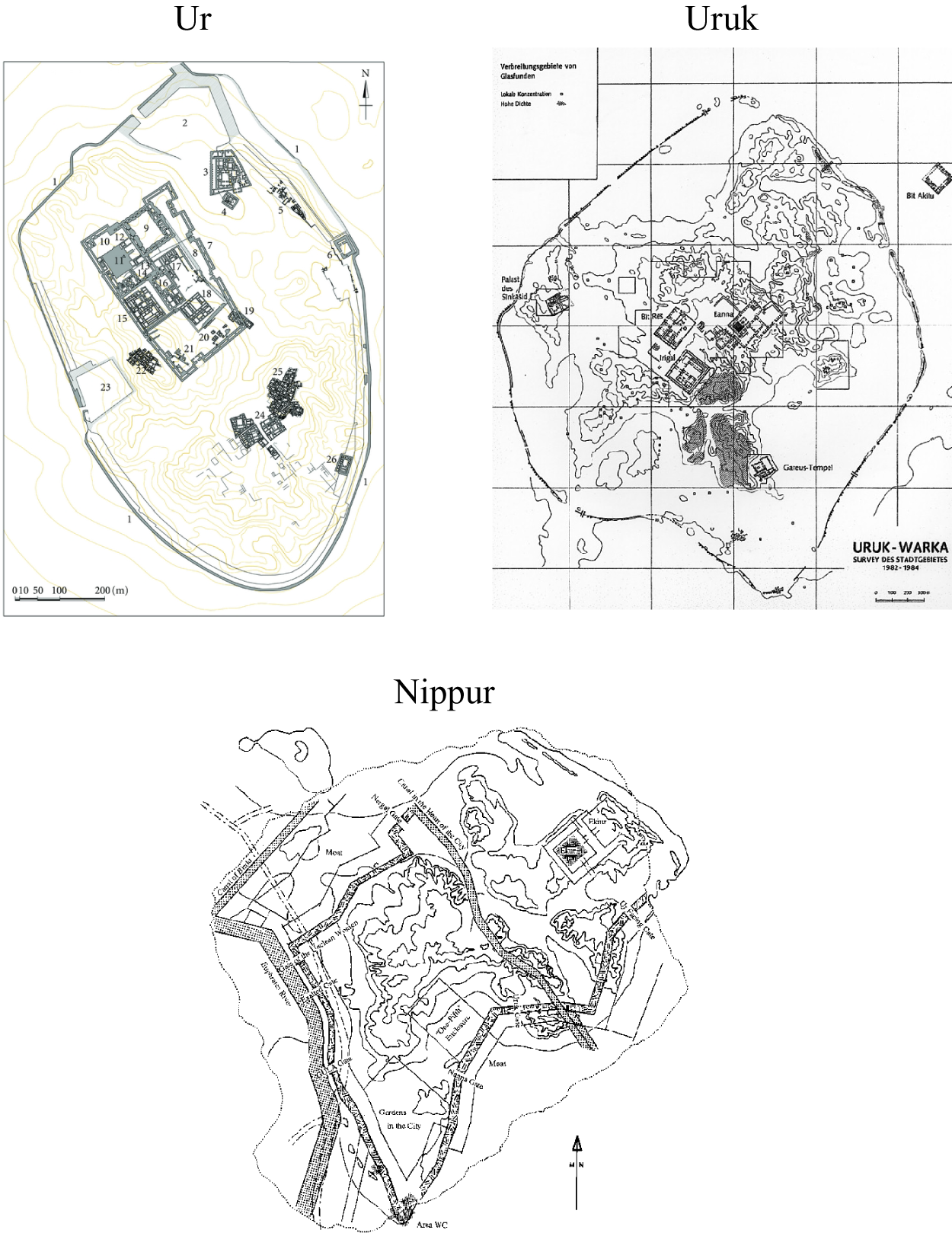
Figure 6. Plans of Sumerian Cities
Sources: Ur: Di Giacomo and Scardozzi (Reference Di Giacomo and Scardozzi2012), drawn by F. Ghio; Uruk: Jordan (Reference Jordan1931); Nippur: Gibson (Reference Gibson1993), drawn by A. McMahon. Plans reproduced with permission where pertinent.
The cost of defense investments in rising city-states was high and would have been prohibitive to societies with low initial incomes. Both walls and the often complementary moats have been estimated to involve large expenses (e.g., the cost estimate for the moat in the Babylonian city of Dur-Jakin is ten thousand men working for three and a half months (Van de Mieroop Reference Van de Mieroop1997, 76). Meeting these high costs surely required a high initial income v 0 (as in Proposition 2). If the presence of defense infrastructure is one empirical requirement to match our model to the Sumerian case, evidence that Sumer had high initial income is the other.
Sumer had high levels of initial income, according to the archaeological consensus in the productivist view (see for instance Algaze Reference Algaze2008; Pollock Reference Pollock1999). Although the Tigris and Euphrates had less attractive properties than the Nile, like two-way navigability and a regular flood pattern, Sumer had favorable conditions for food production. The rivers offered transportation, variation in terms of diet and, as noted above, alluvial agriculture offered high yields even before investments were made. Moreover, the Sumerian territory combined the alluvium with an unparalleled initial endowment of plant and animal domesticates. According to Trigger (Reference Trigger2003, 281), domesticated animals afforded large gains in labor productivity and may have greatly helped develop civilization. Diamond (Reference Diamond1997, Chap. 8) states that all eight founder crops in the Neolithic were present in the area as well as four of the five most important domesticated animals.Footnote 15 The aforementioned properties, fertility, ecological diversity, and plant and animal endowments, map into a high v 0 in our model.
Two Paths to Civilization
The conventional wisdom is that geography played an important role in the rise of both Egypt and Sumer. Most environmental advantages are thought to be common to the two areas. Our model confirms the notion that common growth advantages must have helped Egypt and Sumer. In addition, our model identifies two different paths to civilization depending on how a society solves the political problem of defense. The archaeological record also backs up the interpretation that Egypt and Sumer differed in how they got their defense capabilities. The Egyptians found them in nature, while Sumerians had to build them. This difference is apparent to those familiar with archaeology, but had never been identified as intimately connected to how these two societies escaped the paradox of civilization.
Other Explanations
Since Childe (Reference Childe1936), production optimists have tied the civilization process to developments in agriculture, focusing on the means and relations of production while abstracting from the accompanying innovations in military protection. As described earlier, productivism has molded the conventional wisdom, focusing on the advantages of riverine environments coupled with domesticable plants and animals to explain why some regions generated surpluses while others did not.
Fatalists explicitly connected food production with protection needs (e.g., Mann Reference Mann1986, 48). Their focus on violence implies that security is as crucial as prosperity. Archaeological research attests to the paramount role of investments in protection, such as fortifications, walls, and moats, in the erection of the first cities (see also Service Reference Service1975, 299–300). However, we are not aware of any account that has explicitly focused on the interplay of surplus production and surplus protection to point out a solution to the civilizational paradox.
Important anthropological theories of early states emphasize social stratification and control as defining features.Footnote 16 For example, Fried (Reference Fried1960) espouses the Marxian notion that the state arose as an instrument to consolidate class domination. For Carneiro (Reference Carneiro1970), states originated as growing populations preferred to submit to the authority of inchoate rulers in fertile areas over migrating to less productive land.Footnote 17 The Nile valley, surrounded by deserts, is a good candidate location for such an argument. Our model generates a similar empirical prediction. However, the predicted outcome is not driven by exploitation but by the fact that Egypt’s surrounding deserts were a protective buffer against challengers. In contrast to Carneiro’s theory, our model does not appeal to population pressure, an assumption that has been challenged by other scholars (Allen Reference Allen1997).
The focus on social stratification and control is also present in recent political science work on early states. Mayshar, Moav, and Neeman (Reference Mayshar, Moav and Neeman2017) derive different types of state depending on the observability of production, as this affects the ease with which rulers can raise taxes.Footnote 18 Stasavage (Reference Stasavage, Bisin and Federico2021) considers writing as an instrument of social control. Scott (Reference Scott2017) reviews various arguments on state formation with an emphasis on control by elites over scarce productive land. All of these arguments have merit, as do those by anthropologists focusing on social control. They have in common a focus on the internal dynamics of social hierarchy.
We do not abstract from hierarchy because we think it is unimportant—it was inarguably connected to the process of building the machinery of early states. But we focus on external security for three reasons. First, irrespective of how societies were internally organized, in order to prosper they needed to manage external aggression, which is the problem we analyze. Second, the external security dimension of the early state has received little to no attention. The third reason is methodological: abstracting from hierarchy helps to focus attention on the settler-challenger interaction and extract the insights that emerge exclusively from it.
Conclusion
We focus on civilization as the co-occurrence of two core conditions: prosperity and security. Managing the problem that prosperity attracts predation constituted the first public choice of agricultural settlements and made the rise of civilization not a geographic inevitability but a political possibility.
We study that first public choice through a formal model in the tradition of positive political theory. The choice of components in the model is informed by the historical and archaeological literatures and integrates both productive and defense fundamentals.
Our theory yields three messages. First, the paradox has a solution, against fatalists. Second, against productivists, the solution does not hinge solely on good fundamentals for food production. Civilization is possible if settlements are twice-lucky in terms of their capabilities for growth and defense. Thus, civilization is possible, but should not arise as frequently as we would expect from an exclusive focus on the geography of food production.
Our third message is that civilization could follow two paths, depending on whether defense capabilities were natural or human-made. This provides a new perspective on the emergence of Sumer and Egypt, the first two civilizations. The two cases had one factor in common, and one key difference. The commonality was a high growth capability; the biogeography of both Egypt and Sumer amply rewarded productive investment. The key difference was that Egypt got its protection from the terrain, while Sumerians had to build costly defensive structures. This observation accounts for a major aspect of archaeological remains: the perimeter walls in Sumerian cities were not an epiphenomenon of the civilizational process but a foundational component.
A broader message coming out of our theory is that the paradox of civilization was resolved not by institutions seen as formal rules of the political game but by tangible assets shaped by the geographic environment. Yet, civilization was not the result of geographic determinism. Instead, it arose from settlements optimizing their first public choice concerning the calculus of defense. To the extent that intergroup conflict is what politics looks like before institutions, the rise of civilization was a geopolitical process.
In contrast with theories of early states focusing on internal hierarchy, our theory makes progress by isolating the external defense dimension of statehood as a component of civilization. An interesting path for future research on early states is to formalize the interactions between external defense and internal sociopolitical hierarchy.
Acknowledgments
We thank Robert Allen, Alberto Bisin, Pedro Dal Bó, David de la Croix, Vicky Fouka, Francis Fukuyama, Oded Galor, Andrew Hall, Nicolas Jabko, Becky Morton, Santiago Oliveros, Ben Olken, Demian Pouzo, Robert Powell, Alvaro Sandroni, David Schönholzer, Andrew Schotter, Adam Sheingate, Enrico Spolaore, David Stasavage, Steven Teles, Mathias Thoenig, Thierry Verdier, Romain Wacziarg, Etienne Wasmer, David Weil, Melanie Xue, Noam Yuchtman, and seminar and conference participants at Berkeley, Bocconi, Brown, NBER Political Economy Program, Northwestern, Pompeu Fabra, Princeton, Stanford GSB, and Yale for helpful comments.
Appendix
Proof of Proposition 1: Since the marginal benefit of d
1 goes to infinity as d
1 goes to zero (a typical feature of contests), the optimum must feature d
1 > 0 and
$ {\lambda}_d=0 $
. Therefore, the solution requires checking eight cases in which the remaining three Lagrange multipliers
$ {\lambda}_{BC} $
,
$ {\lambda}_{DC} $
, and
$ {\lambda}_i $
are positive or zero, corresponding to whether each optimization constraint is binding or slack. A tedious but straightforward verification shows that only four cases have consistent solutions as detailed below, and these yield a partition of the parameter space
$ \left({\kappa}_1,\rho, {v}_1\right) $
into two regions:
No civilization potential
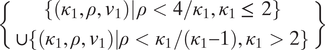$ \left\{\begin{array}{c}\left\{\left({\kappa}_1,\rho, {v}_1\right)|\hskip0.1em \rho <4/{\kappa}_1,{\kappa}_1\hskip2pt \le \hskip4.00pt 2\right\}\\ {}\cup \left\{\left({\kappa}_1,\rho, {v}_1\right)|\rho <{\kappa}_1/\left({\kappa}_1-1\right),{\kappa}_1>2\right\}\end{array}\right\} $
.
This is the dark area below the convex curve in Panel (b) in Figure 3. The convex curve is given by the functions
$ \rho =4/{\kappa}_1 $
(if
$ {\kappa}_1\hskip2pt \le \hskip2pt 2 $
), and
$ \rho ={\kappa}_1/\left({\kappa}_1-1\right) $
(if
$ {\kappa}_1>2 $
). This region is composed of two subregions:
Stagnant Insecurity (Subregion SI):
$ \left\{\left({\kappa}_1,\rho, {v}_1\right)|{\kappa}_1\hskip2pt \le \hskip2pt 2,\rho <4/{\kappa}_1\right\} $
.
Solution:
$ \left\{{d}_1^{\ast }={v}_1{\left(\frac{\kappa_1}{2}\right)}^2,{i}_1^{\ast }=0,{V}_1={v}_1\left(1+\frac{\kappa_1}{4}\right),{a}_1^{\ast }={v}_1\left(\frac{\kappa_1}{2}\right)\left(1-\frac{\kappa_1}{2}\right), CP=0\right\} $
.
Stagnant Security (Subregion SS):
$ \left\{\left({\kappa}_1,\rho, {v}_1\right)|{\kappa}_1>2,\rho <{\kappa}_1/\left({\kappa}_1-1\right)\right\} $
.
Solution:
$ \left\{{d}_1^{\ast }={v}_1,{i}_1^{\ast }=0,{V}_1={v}_1\left(2-\frac{1}{\kappa_1}\right),{a}_1^{\ast }=0, CP=0\right\}. $
Positive civilization potential
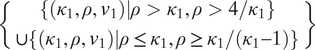$ \left\{\begin{array}{c}\left\{\left({\kappa}_1,\rho, {v}_1\right)|\rho >{\kappa}_1,\rho >4/{\kappa}_1\right\}\\ {}\cup \left\{\left({\kappa}_1,\rho, {v}_1\right)|\rho \hskip2pt \le \hskip2pt {\kappa}_1,\rho \hskip2pt \ge \hskip2pt {\kappa}_1/\left({\kappa}_1-1\right)\right\}\end{array}\right\} $
.
This is the area above the convex curve in Panel (b) in Figure 3. This region is composed of two subregions:
Prosperity Despite Insecurity (Subregion PDI):
$ \left\{\left({\kappa}_1,\rho, {v}_1\right)|\rho >{\kappa}_1,\rho >4/{\kappa}_1\right\} $
.
Solution:
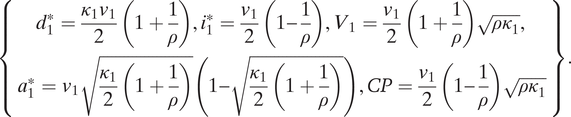$ \left\{\begin{array}{c}{d}_1^{\ast }=\frac{\kappa_1{v}_1}{2}\left(1+\frac{1}{\rho}\right),{i}_1^{\ast }=\frac{v_1}{2}\left(1-\frac{1}{\rho}\right),{V}_1=\frac{v_1}{2}\left(1+\frac{1}{\rho}\right)\sqrt{{\rho \kappa}_1},\\ {}{a}_1^{\ast }={v}_1\sqrt{\frac{\kappa_1}{2}\left(1+\frac{1}{\rho}\right)}\left(1-\sqrt{\frac{\kappa_1}{2}\left(1+\frac{1}{\rho}\right)}\right), CP=\frac{v_1}{2}\left(1-\frac{1}{\rho}\right)\sqrt{{\rho \kappa}_1}\end{array}\right\}. $
Prosperous Security (Subregion PS):
$ \left\{\left({\kappa}_1,\rho, {v}_1\right)|\rho \hskip2pt \le \hskip2pt {\kappa}_1,\rho \hskip2pt \ge \hskip2pt {\kappa}_1/\left({\kappa}_1-1\right)\right\} $
.
Solution:
$ \left\{{d}_1^{\ast }={v}_1\frac{\kappa_1\left(1+\rho \right)}{\kappa_1+\rho },{i}_1^{\ast }={v}_1\frac{\kappa_1-1}{\kappa_1+\rho },{V}_1={v}_1\frac{\kappa_1\left(1+\rho \right)}{\kappa_1+\rho },{a}_1^{\ast }=0, CP=\rho {v}_1\frac{\kappa_1-1}{\kappa_1+\rho}\right\}. $
We restrict attention to the bidimensional space
$ \left({\kappa}_1,\rho \right) $
because the shape of the four regions is invariant in v
1 (although attack intensity
$ {a}_1^{\ast } $
(weakly) increases in v
1). Inspection of the convex frontier {
$ \rho =4/{\kappa}_1 $
if
$ {\kappa}_1\hskip2pt \le \hskip2pt 2 $
,
$ \rho ={\kappa}_1/\left({\kappa}_1-1\right) $
if
$ {\kappa}_1>2 $
} reveals that a low enough
$ \rho $
or κ
1 precludes civilization: areas with high
$ \rho $
but low κ
1 yield Stagnant Insecurity and areas with high κ
1 but low
$ \rho $
yield Stagnant Security; since
$ {i}_1^{\ast }=0 $
in those subregions,
$ {v}_2^{\ast }-{v}_1=0 $
and civilization potential is zero regardless of v
1. Using
$ {d}_1^{\ast } $
,
$ {i}_1^{\ast } $
into the civilization potential
$ CP=\frac{d_1^{\ast }}{d_1^{\ast }+{a}_1^{\ast }}\left({v}_2^{\ast }-{v}_1\right) $
also establishes that civilization potential rises to positive and increasing levels as
$ \left(\rho, {\kappa}_1\right) $
rise above the convex frontier. This establishes the first part of the proposition. In the regions PS and PDI, civilization potential is positive and increasing in v
1 (differentiation shows immediately that
$ \frac{\mathbf{d} CP}{\mathbf{d}{v}_1}>0 $
), yielding the second part of the proposition.■
Proof of Proposition 2: We focus on the case where the settler would be unable to exit the SI subregion in the absence of improvements in defense capabilities. This involves the technical requirement that
$ {\kappa}_0\rho \left(1+\rho \right)<4 $
and
$ {\kappa}_0<2 $
. From the expressions for V
1 in Proposition 1, as the incumbent lands, in t = 1, in each of the subregions PS-SS, the value V
1 is
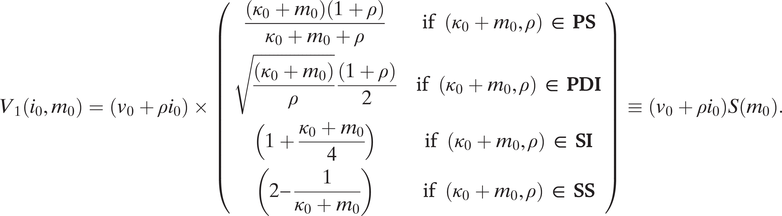$$ {V}_1\left({i}_0,{m}_0\right)=\left({v}_0+\rho {i}_0\right)\times \left(\begin{array}{cc}\frac{\left({\kappa}_0+{m}_0\right)\left(1+\rho \right)}{\kappa_0+{m}_0+\rho }& \mathrm{if}\hskip0.4em \left({\kappa}_0+{m}_0,\rho \right)\hskip0.4em \in \hskip0.4em \mathbf{PS}\\ {}\sqrt{\frac{\left({\kappa}_0+{m}_0\right)}{\rho }}\frac{\left(1+\rho \right)}{2}& \mathrm{if}\hskip0.4em \left({\kappa}_0+{m}_0,\rho \right)\hskip0.4em \in \hskip0.4em \mathbf{PDI}\\ {}\left(1+\frac{\kappa_0+{m}_0}{4}\right)& \mathrm{if}\hskip0.4em \left({\kappa}_0+{m}_0,\rho \right)\hskip0.4em \in \hskip0.4em \mathbf{SI}\\ {}\left(2-\frac{1}{\kappa_0+{m}_0}\right)& \mathrm{if}\hskip0.4em \left({\kappa}_0+{m}_0,\rho \right)\hskip0.4em \in \hskip0.4em \mathbf{SS}\end{array}\right)\equiv \left({v}_0+\rho {i}_0\right)S\left({m}_0\right). $$
Once m
0 is set, the problem of choosing (d
0, i
0) to solve the program in (10) is analogous to the choice of (d
1, i
1) in the baseline model, except now the continuation value depends explicitly on m
0 through S(m
0). Straightforward (and again, tedious) verification shows that only two of the eight cases for whether
$ {\lambda}_{BC} $
,
$ {\lambda}_{DC} $
, and
$ {\lambda}_i $
are positive or zero hold. Both cases feature
$ {i}_0^{\ast }=0 $
, and two levels of defense
$ {d}_0 $
obtain depending on whether m
0 exceeds a level denoted with
$ \overline{m} $
. When
$ {m}_0<\overline{m} $
(so that
$ \frac{v_0S\left({m}_0\right)}{\left({v}_0-{m}_0\right)}<\frac{4}{\kappa_0} $
), we have
$ {d}_0=\frac{\kappa_0^2}{4}{v}_0S\left({m}_0\right) $
(Case 1), and if
$ {m}_0\hskip0.3em \ge \hskip0.3em \overline{m} $
(so that
$ \frac{v_0S\left({m}_0\right)}{\left({v}_0-{m}_0\right)}>\frac{4}{\kappa_0} $
), we have
$ {d}_0={\kappa}_0\left({v}_0-{m}_0\right) $
(Case 2).
If v
0 is low enough, resources are insufficient to move away from region SI and away from Case 1 where
$ \frac{v_0S\left({m}_0\right)}{\left({v}_0-{m}_0\right)}<\frac{4}{\kappa_0} $
. Then, expected utility for the settler is
$ {V}_0={v}_0-{m}_0+\frac{\kappa_0}{4}{v}_0S\left({m}_0\right)={v}_0-{m}_0+\frac{\kappa_0}{4}{v}_0\left(1+\frac{\kappa_0+{m}_0}{4}\right) $
. Since V
0 decreases in m
0 for v
0 small enough, the settler chooses
$ {m}_0^{\ast }=0 $
and stays in region SI. We next show that if v
0 is high enough, the settler chooses m
0 > 0 to land in region PS in t = 1, which yields positive civilization potential. We show this for the case
$ \rho $
< 2 (the case with
$ \rho $
≥ 2 is analogous). Starting in region SI, increases in m
0 take the settler first into region SS and then PS. It is easy to show that if
$ {v}_0>\frac{\frac{4}{\kappa_0}\left(\frac{\rho }{\rho -1} - {\kappa}_0\right)}{\frac{4}{\kappa_0} - \frac{1+\rho }{\rho }} $
, then
$ \overline{m} $
is above the level that takes the settler from SS to PS. Therefore, everywhere in SI and SS the expected utility of the incumbent corresponds to Case 1 but in PS expected utility switches to that corresponding to Case 2 for
$ {m}_0\hskip0.3em \ge \hskip0.3em \overline{m} $
. Some algebra shows that if
$ {v}_0>{\left(\frac{\rho }{\rho -1}\right)}^2\frac{4}{\kappa_0} $
,
$ {V}_0 $
increases in m
0 as long as κ
1 lies in SI and SS. Therefore, the settler will choose m
0 to be high enough that κ
1 will at least weakly enter region PS. In addition, it is easy to show that V
0 is initially increasing and concave in m
0 in region PS. Therefore, if v
0 is high enough the optimal solution
$ {m}_0^{\ast } $
places the settler in the interior of PS, guaranteeing positive civilization potential in t = 1 (which, from Proposition 1, increases in
$ \rho $
). ■
Open access
Comments
No Comments have been published for this article.