Article contents
The Desired Political Entropy
Published online by Cambridge University Press: 01 August 2014
Extract
In an article published in the December 30, 1967 issue of the Dutch weekly magazine Vrij Nederland, Mr. Frans Grosfeld suggested the following modification of the procedure of parliamentary representation of political parties. Instead of the conventional method of allocating to each party a number of representatives proportional to the number of votes cast for the party, he proposed to allocate a number of representatives which is proportional to the square of the number of votes. Thus, when there are n parties and when p1, …, pn are the proportions of the total number of votes obtained by these parties, the idea is to allocate a fraction qi of the representatives to the ith party determined by
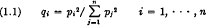
Mr. Grosfeld made this suggestion for the Dutch political system, because in his view n is so large and even the largest pi belongs to a minority party, so that on many occasions several months of negotiations were necessary to obtain a coalition cabinet of one form or another. By squaring the pi's one obtains much larger relative differences between the larger and the smaller parties, and one party or a pair of politically related parties then has a much better chance of obtaining a parliamentary majority. Also, the system (1.1) provides an incentive for parties to merge, which contributes to a reduction of the degree to which the country is politically divided. This system should be contrasted with another system which is applied on a rather large scale, viz., that of declining any seat to those parties whose pi is less than a pre-assigned fraction θ (for example, θ = .03).
- Type
- Research Notes
- Information
- Copyright
- Copyright © American Political Science Association 1969
References
1 Since the number of representatives allocated to each party must be a nonnegative integer, the actual q i's will be slightly different from those defined in (1.1) and (1.2). This feature will be disregarded in the present note, but it should be stressed that the criterion used in Section 2—the minimization of the information expectation defined in eq. (2.4)—can be used to handle this problem. The approach is then to minimize the information expectation subject to the constraint that each q i,- be a nonnegative multiple of 1/N, where N is the total number of parliamentary seats.
2 Plus the case α = ∞ (i.e., allocating all seats to the ruling party), a procedure used in some of the democratically less advanced countries.
3 For a brief introduction to the informational concepts used in this section, see e.g. Chapters 1 and 2 of the author's Economics and Information Theory (Chicago: Rand McNally and Company, and Amsterdam: North-Holland Publishing Company, 1967)Google Scholar. The idea of using the entropy for this particular purpose is due to Mr. B. M. S. van Praag of the Econometric Institute in Rotterdam.
4 Even for n = 2 the entropy does not determine the q's uniquely, because (θ, 1–θ) and (1–θ, θ) have the same entropy for any θ in the interval (0, 1). It is obvious, however, that the present discussion loses much of its interest when n = 2 instead of n > 2.
5 This becomes particularly clear when I(q:p) is expanded according to powers of (q i–p i)/p i. If we use natural logarithms (which is done throughout this paper) and disregard third and higher powers, the result is
provided that the p's and q's are pairwise sufficiently close to each other (so that the expansions converge). The right-hand side of this approximation is proportional to a chi-square with the p's as theoretical probabilities and the q's as observed frequencies.
6 To make the discussion more concrete, we will talk about parties and parliamentary seats rather than about both these and the geographic representations such as those of IFORS and the U.S. Senate.
7 Write p 1 for the largest p i, then q 1 converges to 1 as α → ∞, so that H q = 0 in the limit. If p 1 =p 2 and if all other p i's are smaller, then q 1 = q 2 = ½ in the limit and hence H q>0 even when α = ∞. In the case of a k-fold multiple maximum, p 1 = … = p k>p k+1 ≥ … ≥p n, the interval for H q mentioned in Theorem 1 should be confined to (log k, log n).
8 By substituting log q i for α log p i – log C in the second line of (2.12) we obtain a result that can be written as follows:
which means that a small relative increase in α reduces the entropy H q by k times this increase, where k is the variance of the distribution whose values are –log q 1, … , –log q n and whose probabilities are q 1, …, q n. Obviously, the mean of this distribution is the entropy H q.
9 For details, see e.g. Economics and Information Theory (quoted in footnote 3), p. 7, or Koopman, B. O. and Kimball, G. E., “Information Theory,” Chapter 9 of Notes on Operations Research 1959, assembled by the Operations Research Center, Massachusetts Institute of Technology (Cambridge, Mass.: The Technology Press, M.I.T., 1959)Google Scholar.
10 This will of course require the teaching of logarithms at an early stage. Mathematics teachers should regard it as a challenge to teach a subject with immediate political science applications.
- 29
- Cited by



Comments
No Comments have been published for this article.