1. INTRODUCTION
Increasing complexity of products design and fierce competition of market have always led to the search for reuse historical design knowledge to integrate solutions of new discovered functions into a structure or explore multidisciplinary knowledge to stimuli novel promising solutions (Chen et al., Reference Chen, Liu and Xie2012). Conceptual design is defined as the phase in which the design requirements are described and promising solutions are generated. Studies show that about 70%–80% of the product life cycle cost is determined in conceptual design (Kota & Lee, Reference Kota and Lee1993). Moreover, it is pivotal in defining new, creative products for the sake of it is hard to smooth a poor conceptual design decision in the following stages. Research to support creative conceptual design has been widely reported for decades (Liu et al., Reference Liu, Li, Pan and Li2011). Many creative conceptual design models have been proposed, which can be classified into design strategies centered models and knowledge reuse centered models. Design strategies centered models prompt design solutions generation by using various novel ideas creation strategies. Examples include the genetic algorithm based model (Santillan-Guiterrez & Wright, Reference Santillan-Gutierrez, Wright and Sharpe1996), the case-based reasoning (CBR) model (Gero, Reference Gero1990; Goel, Reference Goel1997; Yang & Chen, Reference Yang and Chen2011), the hierarchical decomposition and recomposition based model (Chakrabarti & Blessing, Reference Chakrabarti and Blessing1996; Li et al., Reference Li, Hu and Peng2010), the function–behavior–structure (FBS) model and its extensions (Goel, Reference Goel1997, Reference Goel and Bhatta2004; Gero, Reference Gero2000; Gero & Kannengiesser, Reference Gero and Kannengiesser2007; Ma et al., Reference Ma, Hu, Zheng and Peng2013), and the TRIZ based model (Becattini, Reference Becattini, Borgianni, Cascini and Rotini2012). Knowledge reuse centered models aim at modeling and reuse design knowledge for exploring design knowledge previously unknown to the designers. Examples include the axiomatic design model (Suh, Reference Suh2001), the intelligent creative conceptual design (ICCD) model (Chen et al., Reference Chen, Liu and Xie2012), and the heuristic based model (Stone et al., Reference Stone, Wood and Crawford2000; Chong et al., Reference Chong, Chen and Leong2009). However, these models focus on research of practical methods of products design and emphasize partial optimization of the design process. The research of a combined approach for creative conceptual design is neglected.
The objective of this paper is to support creative conceptual design by proposing a combined approach, including a unified consistent knowledge representation model that can be applied to a multidiscipline environment, a hybrid similarity measure that realizes multidisciplinary knowledge retrieval, and an intelligent creative conceptual design system (ICCDS) that supports creative conceptual design directly. The remainder of this paper is organized as follows. Section 2 is a literature review on CBR based creative conceptual design models and similarity measures for case retrieval. Section 3 describes key techniques of the proposed approach, including FBS knowledge cell construction, the adapted CBR model, and the hybrid similarity measure. Section 4 presents the implementation of the combined approach, a case study of ICCDS, and its performance evaluation. Finally, the conclusions are given in Section 5.
2. LITERATURE REVIEW
CBR is a problem-solving paradigm that retrieves, reuses, and revises historical cases to fulfill new design requirements through imitating the problem-solving mechanism of human beings. Comparing with other major creative conceptual design models, CBR has several advantages: it enables learning nonlinearly separable categories and continuous functions with low computational cost, it simulates a practical scientific reasoning process of human beings that is human understandable, and it supports multidomains knowledge reuse successfully (Liu & Chen, Reference Liu and Chen2012). Goel and Bhatta (Reference Goel and Bhatta2004) proposed a model based analogy to transfer design patterns of sources to address creative design problems. Han and Lee (Reference Han and Lee2006) presented a case-based computational framework for design synthesis that implemented virtual function generators as reusable design blocks to generate novel design solutions. Yang and Chen (Reference Yang and Chen2011) described a novel model to accelerate ecoinnovation product design by integrating advantages of CBR and TRIZ. Janthong et al. (Reference Janthong, Brissaud and Butdee2010) combined axiomatic design principles with CBR for mechatronics products design. However, these models focus on creation design strategies research and pay little attention to defining a consistent knowledge representation model, lowering the reusability of design knowledge. The FBS model (Gero, Reference Gero1990) is one of the first functional models that represent design cases, for example, products or artifacts, in terms of function. It supports conceptual design by taking hierarchical functional decomposition as the bridge between high-level design requirements and low-level detailed structure representation and provides design process with a consistent knowledge representation model. It can realize exploration of the innovative space of the products between different design fields fleetly through adopting casual mapping between design elements as the driver. Other researchers have described similar models based on the triplet of knowledge (function, behaviour, and structure) with modifications, such as the FBS model of Umeda and Tomiyama (Reference Umeda and Tomiyama1995), the structure–behavior–function model of Goel (Reference Goel1997; Goel & Bhatta, Reference Goel and Bhatta2004), the function effect behavior structure model of Deng (Reference Deng2002), and the requirement function behavior structure of Christophe et al. (Reference Christophe, Bernard and Coatanéa2010). However, more attention should be paid to proper tools and strategies for design knowledge reuse. Considering the characteristics of the above models, this paper integrates Gero's FBS model into the CBR paradigm and attempts to create a fusion of their advantages. A consistent design knowledge representation model, named the FBS knowledge cell model, is designed to better represent and reuse design knowledge. The design strategies of CBR are retained to facilitate the design process while employing FBS knowledge cells instead of case families as design knowledge carriers to realize product design.
The case retrieval process is pivotal in finding the most similar cases to provide immediate ideas or useful design knowledge. Most applications of case retrieval use the nearest neighbors to measure the similarity between specified design requirements and stored cases considering various types of knowledge representation. Thus, the selection of similarity measures and its weighting methods has been among the most popular research issues (Liu & Chen, Reference Liu and Chen2012). Contents of design knowledge can be mainly classified into two categories: numeric expression knowledge and semantic description knowledge. Commonly, distance functions derived from Euclidean distance or Manhattan distance (Qi et al., Reference Qi, Hu, Peng, Wang and Zhang2009) are implemented for numeric expression knowledge matching. Meanwhile, similarity evaluation of semantic description knowledge is always conducted by computing the similarity between terms. Existing semantic similarity measures can be categorized into node distance (ND) based measures, information content (IC) based measures, and hybrid measures (Li et al., Reference Li, Bandar and McLean2003). ND measures similarity through statistics and the shortest path distances between lexicon terms. However, nonuniform link strength between adjacent terms affects its reliable, and the accuracy of ND yields 60%. For example, IS-A links: Tesla IS-A Machine and Car IS-A Vehicle, the IS-A link between the former covers a larger conceptual distance than the latter. IC is conducted on the premise that the sharing information of two lexicon terms is proportionate to their similarity, with an accuracy of 82%. Hybrid measures inherit the edge counting schema of ND and implement the information content calculation of IC as a decision factor to develop a combined similarity measure that improves the semantic similarity calculation accuracy up to 87% (Jiang & Conrath, Reference Jiang and Conrath1997). Liao et al. (Reference Liao, Zhang and Mount1998) developed a hybrid similarity measure for similarity calculation with a mixture of crisp and fuzzy features. Qi et al. (Reference Qi, Hu, Peng, Wang and Zhang2009) used triangular functions for fuzzy numeric knowledge and fuzzy linguistic knowledge evaluation. Based on the NIST functional basis taxonomy, Fernandes et al. (Reference Fernandes, Grosse, Krishnamurty, Witherell and Wileden2011) presented the semantic relatedness uniqueness metric to provide designers a measure of their effectiveness by generating unique design concepts. Hu et al. (Reference Hu, Hu, Peng and Cao2012) proposed a two-level clustering algorithm for case retrieval considering four types of design knowledge: numeric, linguistic terms, fuzzy sets, and Boolean. Guo et al. (Reference Guo, Hu and Peng2012) proposed a hybrid similarity measure for injection mold design based on ontology. Fan et al. (Reference Fan, Li, Wang and Liu2014) proposed a hybrid similarity measure considering the situation of five formats, including crisp symbol, crisp number, interval number, fuzzy linguistic, and random variable, and gave a systematic literature review on proposed similarity measurements of numeric expression. However, little attention has been paid to the hybrid similarity measure considering both numeric expression and semantic description, and semantic understanding ability is lacking. Therefore, an in-depth study of a hybrid similarity measure is worthwhile.
3. KEY TECHNIQUES OF THE INTELLIGENT CBR SYSTEM
3.1. Adapted CBR model using FBS knowledge cells
The CBR model uses FBS knowledge cells as function blocks to produce novel design ideas, as given in Figure 1. It starts right after extracting required functions from design requirements and is followed by searching the FBS knowledge cell library to obtain a set of similar knowledge cells. Then the designer attempts to reuse the retrieved FBS knowledge cells after adapting them. Once no satisfied FBS knowledge cell is retrieved, designer should further decompose the required function into subfunctions and repeat the retrieval process. When all required functions obtain their suitable FBS knowledge cells, the retrieved knowledge cells will be recomposed by a backtracking function decomposition process to arrive at suggested solutions. If necessary, designers revise or adapt the suggested solutions after further evaluating the quality of generated design solutions. Finally, the output design solutions are retained as a new design experience and added into the FBS knowledge cell library. Compared with the traditional CBR model, there are two main differences: using the FBS knowledge cell library as a knowledge base instead of cases family, and hierarchical function decomposition to retrieve suitable FBS knowledge cells and recomposition of the retrieved FBS knowledge cell to build suggested solutions. These differences are convenient to understand and reuse design knowledge.
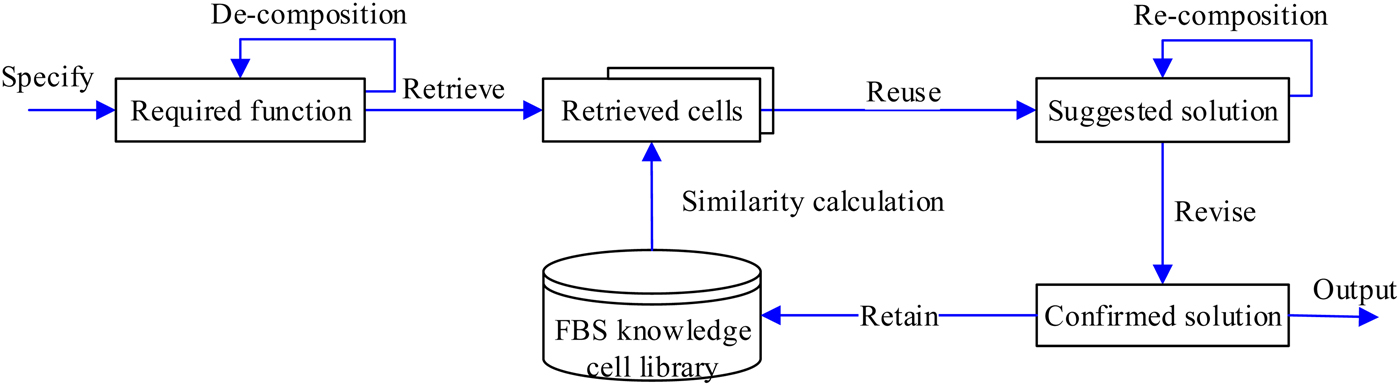
Fig. 1. The adapted CBR model uses FBS knowledge cell.
3.2. FBS knowledge cell representation schema
Based on the function knowledge decomposition theory and function knowledge cell (FKC)/function microknowledge cell (FMKC) given by Li et al. (Reference Li, Hu and Peng2010), an approach of FBS knowledge cell is proposed. There are two significant advantages in Li's model: function knowledge decomposition theory offers a method to judge the endpoint of function decomposition to decompose a complex mechanism into simpler function blocks as well as guarantee reusability and robustness of obtained knowledge cells; and FKC/FMKC provides the design process with a unified consistent knowledge representation schema that facilitates multidisciplinary knowledge storage, manipulation, retrieve, and reuse. However, FKC/FMKC integrates function representation with structure representation but neglects separation of behavior from function, which plays a vital role in offering design procedures with reasons behind the structure and with casual relations among the states or behavior variables. Because confusion and mixing of behavior and function lower the reusability of design knowledge, it is necessary to separate them (Sasajima et al., Reference Sasajima, Kitamura and Ikeda1995). For example, the function of a hydraulic cylinder, whose behavior is to convert hydraulic pressure into mechanical energy and vice versa, becomes different when it is planted in different equipment. When it is used in lifting equipment to realize the function lift object, its behavior is “to realize reciprocating motion and maintain stability movement of plunger.” When it is used in buffer device to absorb shock, its behavior becomes “to absorb the vibration energy and to protect the equipment from being affected and damaged.” In this study, the process of modeling FBS knowledge cell is given in Figure 2. The FBS knowledge cell is designed by building function–behavior mapping and behavior–structure mapping to integrate behavior knowledge with obtained FS knowledge cells in modeling the FMKC process.

Fig. 2. Integrating behavior knowledge with FS knowledge cell to build FBS knowledge cell.
FBS knowledge cell representation describes essential design knowledge and possesses internal links to corresponding elaborate function, behaviour, and structure representation. The FBS knowledge cell representation schema is given in Figure 3. In the schema, function reveals the abstract of specific capability that the system can achieve. Pahl and Beitz's (Reference Pahl and Beitz1988) syntax of transitive verb + noun + complement and transitive verb lexicon defined by Stone et al. (Reference Stone, Wood and Crawford2000) are adopted in function name representation to avoid ambiguity. Driving _input and Function _output flow (Stone et al., Reference Stone, Wood and Crawford2000) state the formal definition of input and output flow of energy (E), signal (S), and material (M) required by design systems. An additional description is added in Annotation to provide designers with more essential design knowledge. Behavior representation pertains to the structure and realizes its function. It describes intermediate states of structures or mechanisms and provides the design process with more precise design knowledge on how the structure behaves in achieving a certain function. Structure describes basic geometry information in terms of parametric representation and semantic description. Working as function blocks, sets of obtained FBS knowledge cells are saved in a FBS knowledge cell library hierarchically according to the decomposition process.

Fig. 3. FBS knowledge cell representation.
3.3. Proposed hybrid similarity measures for case retrieval
FBS knowledge cell retrieval is the key phase in the proposed CBR model where the assessment of similarity between required functions and target FBS knowledge cells plays a vital role because near-most or most suitable solutions can be retrieved and ranked if superior similarity measures exist. During the retrieval process, the required functions are specified in the form of attribute-value pairs plus additional semantic descriptions [Eq. (1)]. Attributes are represented in the form of semantic descriptions, values are given either semantically or numerically, and the additional semantic description is given to provide more retrieval information. The specified function ![]() ${{\rm \cal K}}$ can be represented as the following:
${{\rm \cal K}}$ can be represented as the following:
where ![]() ${{\cal S}}$,
${{\cal S}}$, ![]() ${{\cal N}_{\rm C}}\comma\ {\mkern 1mu} {\rm and} \;{\mkern 1mu} {{\cal N}_{\rm F}}$ represent semantic knowledge, the crisp/interval value, and the fuzzy numeric value separately.
${{\cal N}_{\rm C}}\comma\ {\mkern 1mu} {\rm and} \;{\mkern 1mu} {{\cal N}_{\rm F}}$ represent semantic knowledge, the crisp/interval value, and the fuzzy numeric value separately.
3.3.1. FBS knowledge cells preselection
The introduction of preselection aims at narrowing the retrieval range and reducing computation loads in subsequent steps. The set of preselected FBS knowledge cells is determined by retrieving the standard transitive verb vocabulary and flow vocabulary to judge the consistency of verb in Function_ name and Input/output flow of Driving_ input/ Function_ output of ![]() ${F_{\rm C}^{\,j}}$ (the function of the jth FBS knowledge cell in the FBS knowledge cell library
${F_{\rm C}^{\,j}}$ (the function of the jth FBS knowledge cell in the FBS knowledge cell library ![]() $\{{C_{\rm FBS}^{\,p}}\}$) and
$\{{C_{\rm FBS}^{\,p}}\}$) and ![]() ${F_{\rm R}^{\,i}}$ (the ith specified required function). Equation (2) states that the FBS knowledge cell has synonymous verbs and the same input/output flow with the required function preselected. The set of preselected FBS knowledge cells of
${F_{\rm R}^{\,i}}$ (the ith specified required function). Equation (2) states that the FBS knowledge cell has synonymous verbs and the same input/output flow with the required function preselected. The set of preselected FBS knowledge cells of ![]() ${F_{\rm R}^{\,i}}$ is denoted as
${F_{\rm R}^{\,i}}$ is denoted as ![]() $\{{C_{i}^{\,j}}\}$.
$\{{C_{i}^{\,j}}\}$.
 $$\eqalign{{\rm Sim}_{\rm pre}\lpar {\rm \cal S}_{\rm R}\comma\;{\rm \cal S}_{\rm C} \rpar = & \big[ {verb\left(F_{\rm R}^{\,i} \sim F_{\rm C}^{\,j} \right) ?1:0} \big] \cr & \cup \big[ {Inpu{t_{\,flow\left( {F_{\rm R}^{\,i} = F_{\rm C}^{\,j}} \right)}}?1:0} \big] \cr & \cup [ {Output\_\,flow\left( {F}_{\rm R}^{\,i} = {F}_{\rm C}^{\,j}\right) ?1:0} ] \; \lpar {i\hbox{,}\;j \in N} \rpar}. $$
$$\eqalign{{\rm Sim}_{\rm pre}\lpar {\rm \cal S}_{\rm R}\comma\;{\rm \cal S}_{\rm C} \rpar = & \big[ {verb\left(F_{\rm R}^{\,i} \sim F_{\rm C}^{\,j} \right) ?1:0} \big] \cr & \cup \big[ {Inpu{t_{\,flow\left( {F_{\rm R}^{\,i} = F_{\rm C}^{\,j}} \right)}}?1:0} \big] \cr & \cup [ {Output\_\,flow\left( {F}_{\rm R}^{\,i} = {F}_{\rm C}^{\,j}\right) ?1:0} ] \; \lpar {i\hbox{,}\;j \in N} \rpar}. $$3.3.2. Similarity measure for semantic knowledge
To realize multidisciplinary design knowledge retrieval, a broad coverage corpus is required to work as an underlying reference for semantic similarity calculation. Authors typically exploited WordNet, contains around 100,000 terms, as an ontology for natural language terms in measuring semantic similarity between a pair of synsets (George & Christiane, Reference George and Christiane2006). In WordNet, terms with distinct concepts are grouped into different sets of synonyms and interlinked by means of semantic and lexical relations (is-a, part-of, similar, and inverse relations). Motivated by this, this study carried out some new attempts to improve semantic similarity calculation accuracy by combing ND and IC together while using WordNet ontology as a reference, and a three-level semantic similarity calculation approach was proposed.
First-level semantic calculation based on IC
Terms of semantic description are extracted manually from the compared requirordNet based similarity definition with nodes state the terms and links state the relations between terms as shown in Figure 4.
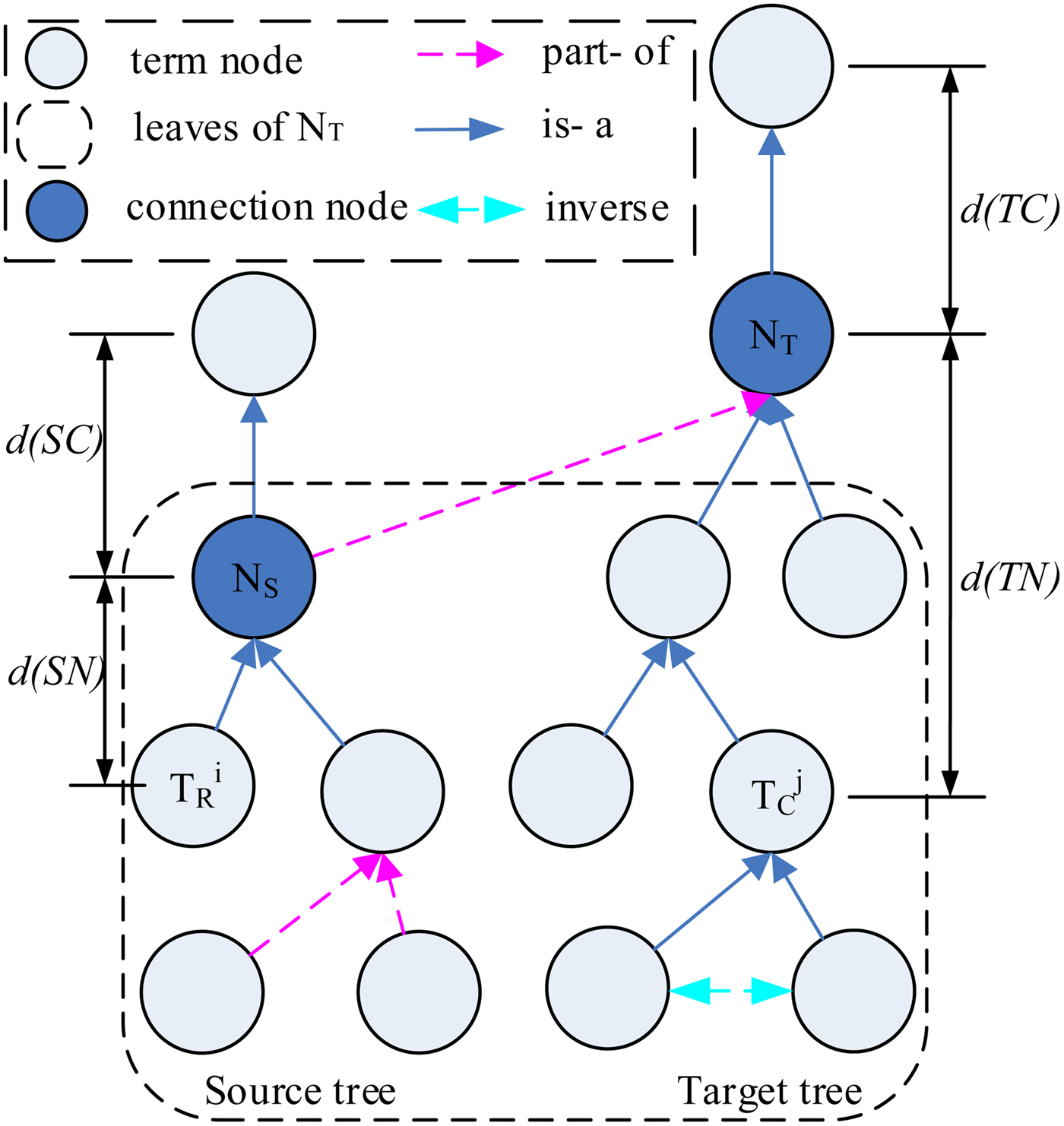
Fig. 4. WordNet based similarity definition.
WordNet based similarity definition with nodes state the terms and links state the relations between terms as shown in Figure 4.
The IC of a term can be quantified as log of the inverse of the probability that it is observed. Similarity of two compared terms is extent to the specific term that subsumes them both in the taxonomy. Therefore, assume the specific term N T that subsumes both ![]() $ T_{\rm R}^{\,i}\in T_{\rm R}$ and
$ T_{\rm R}^{\,i}\in T_{\rm R}$ and ![]() $ T_{\rm C}^{\,j}\in T_{\rm C}$ is the “lowest upper node” among those terms that subsume them. Information content based similarity (
$ T_{\rm C}^{\,j}\in T_{\rm C}$ is the “lowest upper node” among those terms that subsume them. Information content based similarity (![]() ${\rm Sim}_{\rm SS}^{\rm IC} {\lpar {T_{\rm R}^{\,i}\comma\; T_{\rm C}^{\,j}} \rpar _{k}^{\prime\prime}}$) of
${\rm Sim}_{\rm SS}^{\rm IC} {\lpar {T_{\rm R}^{\,i}\comma\; T_{\rm C}^{\,j}} \rpar _{k}^{\prime\prime}}$) of ![]() ${{T_{\rm R}^{\,i} \ {\rm and}\ T_{\rm C}^{\,j}} }$ of the kth pair of compared function can be defined as
${{T_{\rm R}^{\,i} \ {\rm and}\ T_{\rm C}^{\,j}} }$ of the kth pair of compared function can be defined as
 $${\rm Sim}_{{\rm SS}}^{{\rm IC}} {\rm }{\left( {T_{\rm R}^{\,i} \comma\; T_{\rm C}^{\,j} } \right)_k{{\prime\prime}}} = \mathop {\max }\limits_{{N_{\rm T}} \in {\rm Sup}\left( {T_{\rm R}^{\,i} \comma T_{\rm C}^{\,j} } \right)} {\rm }\left\{ { - {\rm log}\left( {{P_{{\rm children}}}\left( {{N_{\rm T}}} \right)} \right)} \right\}\comma $$
$${\rm Sim}_{{\rm SS}}^{{\rm IC}} {\rm }{\left( {T_{\rm R}^{\,i} \comma\; T_{\rm C}^{\,j} } \right)_k{{\prime\prime}}} = \mathop {\max }\limits_{{N_{\rm T}} \in {\rm Sup}\left( {T_{\rm R}^{\,i} \comma T_{\rm C}^{\,j} } \right)} {\rm }\left\{ { - {\rm log}\left( {{P_{{\rm children}}}\left( {{N_{\rm T}}} \right)} \right)} \right\}\comma $$where P children(N T) is the probability of occurrence of all terms derived from N T (including itself) and P children(N T) = (0, 1].
When all IC based similarities oeach compared term pair have been obtained, normalized similarities ![]() ${\rm Sim}_{{\rm SS}}^{{\rm IC}} {\lpar {T_{\rm R}^{\,i}\comma\; T_{\rm C}^{\,j}} \rpar _k}$ can be calculated by implementing Eq. (4) to keep the value between 0 and 1.
${\rm Sim}_{{\rm SS}}^{{\rm IC}} {\lpar {T_{\rm R}^{\,i}\comma\; T_{\rm C}^{\,j}} \rpar _k}$ can be calculated by implementing Eq. (4) to keep the value between 0 and 1.
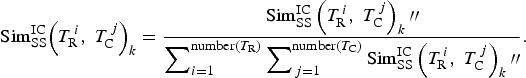 $${\rm Sim}_{{\rm SS}}^{{\rm IC}} {\left( {T_{\rm R}^{\,i} \comma\; T_{\rm C}^{\,j} {\rm }} \right)_k} = \displaystyle{{{\rm Sim}_{{\rm SS}}^{{\rm IC}} {\rm }\left( {T_{\rm R}^{\,i} \comma\; T_{\rm C}^{\,j} } \right)_k{{\prime\prime}}} \over {\displaystyle\sum\nolimits_{i = 1}^{{\rm number}\left( {{T_{\rm R}}} \right)} {\displaystyle\sum\nolimits_{\,j = 1}^{{\rm number}\left( {{T_{\rm C}}} \right)} {{\rm Sim}_{{\rm SS}}^{{\rm IC}} } } {\rm }\left( {T_{\rm R}^{\,i} \comma\; T_{\rm C}^{\,j} } \right)_k{{\prime\prime}}}}. $$
$${\rm Sim}_{{\rm SS}}^{{\rm IC}} {\left( {T_{\rm R}^{\,i} \comma\; T_{\rm C}^{\,j} {\rm }} \right)_k} = \displaystyle{{{\rm Sim}_{{\rm SS}}^{{\rm IC}} {\rm }\left( {T_{\rm R}^{\,i} \comma\; T_{\rm C}^{\,j} } \right)_k{{\prime\prime}}} \over {\displaystyle\sum\nolimits_{i = 1}^{{\rm number}\left( {{T_{\rm R}}} \right)} {\displaystyle\sum\nolimits_{\,j = 1}^{{\rm number}\left( {{T_{\rm C}}} \right)} {{\rm Sim}_{{\rm SS}}^{{\rm IC}} } } {\rm }\left( {T_{\rm R}^{\,i} \comma\; T_{\rm C}^{\,j} } \right)_k{{\prime\prime}}}}. $$Second-level semantic similarity calculation based on ND
In this study, ND based similarity calculation takes not only hierarchical node depth related link strength but also distinct relations related link strengths into consideration.
1. Hierarchical node depth related link strength. Under considering the semantic difference of different links in different layers, hierarchical node depth related link strength between adjacent terms T s and T sub(s) can be formally defined as
(5)where d(T sub(s)) represents the depth of T sub(s) from the root node to node T sub(s) and T sub(s) is the subnode of T s. The choice of root node depends on the specific term N T. $${{\rm \omega} _{\rm s}}({T_{\rm s}}\comma\; {T_{{\rm sub}\lpar s \rpar })} = 1 + 1/{2^{\lpar {d\lpar {{T_{{\rm sub}\lpar s \rpar }}} \rpar - 1} \rpar }}$$
$${{\rm \omega} _{\rm s}}({T_{\rm s}}\comma\; {T_{{\rm sub}\lpar s \rpar })} = 1 + 1/{2^{\lpar {d\lpar {{T_{{\rm sub}\lpar s \rpar }}} \rpar - 1} \rpar }}$$2. Distinct relations related similarity. Distinct relations between two adjacent terms have different link strength. The weights of the distinct relations are assigned in the following order: exact match (µe = 1) > similar (µm) > is-a (µis) > part-of (µp) > inverse (µin = 0). Values of relations weights are obtained through experiments or related domain experts (empirically set µm = 0.86, µis = 0.64, µp = 0.36).
Node distance is the product of hierarchical node depth related link strength and distinct relations related link strength. The node distance algorithm is given in Figure 5.

Fig. 5. Pseudocode for nodes distance algorithm.
In order to transform the node distance into a similarity, the inverted function is introduced. Thus, ND similarity (![]() ${\rm Sim}_{{\rm SS}}^{{\rm ND}} {\lpar {T_{\rm R}^{i}\comma\; T_{\rm C}^{\,j}} \rpar _k}$) of terms
${\rm Sim}_{{\rm SS}}^{{\rm ND}} {\lpar {T_{\rm R}^{i}\comma\; T_{\rm C}^{\,j}} \rpar _k}$) of terms ![]() ${{T_{\rm R}^{i}} }$ and
${{T_{\rm R}^{i}} }$ and ![]() $T_{\rm C}^{j}$ of the kth compared functions pair is calculated implementing Eq. (6).
$T_{\rm C}^{j}$ of the kth compared functions pair is calculated implementing Eq. (6).
 $${\rm Sim}_{{\rm SS}}^{{\rm ND}} {\lpar {T_{\rm R}^{\,i}\comma\; T_{\rm C}^{\,j}} \rpar _k} = \displaystyle{1 \over {{\rm ND}{{\lpar {T_{\rm R}^{\,i}\comma\; T_{\rm C}^{\,j}} \rpar }_k} + 1}}.$$
$${\rm Sim}_{{\rm SS}}^{{\rm ND}} {\lpar {T_{\rm R}^{\,i}\comma\; T_{\rm C}^{\,j}} \rpar _k} = \displaystyle{1 \over {{\rm ND}{{\lpar {T_{\rm R}^{\,i}\comma\; T_{\rm C}^{\,j}} \rpar }_k} + 1}}.$$
The total semantic similarity of compared terms ![]() ${{T_{\rm R}^{\,i} \ {\rm and}\ T_{\rm C}^{\,j}} }$ can be defined as
${{T_{\rm R}^{\,i} \ {\rm and}\ T_{\rm C}^{\,j}} }$ can be defined as
 $$\eqalign{{\rm Si}{{\rm m}_{{\rm SS}}}{\lpar {T_{\rm R}^{\,i}\comma\; T_{\rm C}^{\,j}} \rpar _k} & = {\rm \gamma} \times {\rm Sim}_{{\rm SS}}^{{\rm IC}} {\lpar {T_{\rm R}^{\,i}\comma\; T_{\rm C}^{\,j}} \rpar _k} + \lpar {1 - {\rm \gamma}} \rpar \cr & \quad \times {\rm Sim}_{{\rm SS}}^{{\rm ND}} {\lpar {T_{\rm R}^{\,i}\comma\; T_{\rm C}^{\,j}} \rpar _k}}, $$
$$\eqalign{{\rm Si}{{\rm m}_{{\rm SS}}}{\lpar {T_{\rm R}^{\,i}\comma\; T_{\rm C}^{\,j}} \rpar _k} & = {\rm \gamma} \times {\rm Sim}_{{\rm SS}}^{{\rm IC}} {\lpar {T_{\rm R}^{\,i}\comma\; T_{\rm C}^{\,j}} \rpar _k} + \lpar {1 - {\rm \gamma}} \rpar \cr & \quad \times {\rm Sim}_{{\rm SS}}^{{\rm ND}} {\lpar {T_{\rm R}^{\,i}\comma\; T_{\rm C}^{\,j}} \rpar _k}}, $$
where γ is the weight of information content based semantic similarity![]() $\; {\rm Sim}_{{\rm SS}}^{{\rm IC}} {\lpar {T_{\rm R}^{\,i}\comma\; T_{\rm C}^{\,j}} \rpar _k}$. Considering ND is not very reliable and according to experiment results, the value of r is about [0.85, 0.95].
$\; {\rm Sim}_{{\rm SS}}^{{\rm IC}} {\lpar {T_{\rm R}^{\,i}\comma\; T_{\rm C}^{\,j}} \rpar _k}$. Considering ND is not very reliable and according to experiment results, the value of r is about [0.85, 0.95].
Third-level global semantic similarity calculation based on TF-IFF
The above semantic similarity considers similarity of compared terms. However, the term frequency of occurrence is another factor that should be considered. TF–inverse document frequency (TF-IDF; Salton & Buckley, Reference Salton and Buckley1988) is the common way of term weighting. TF-IDF increases proportionally to the probability of occurrence of a term in the document, but it is offset by the term frequency in the corpus. The original thought of TF-IDF is borrowed here, and some modifications are made to reflect our intensions. Given Tt ∈ T C and ![]() ${{C_{i}^{\,j}} }$, the term frequency TFt,j is calculated as
${{C_{i}^{\,j}} }$, the term frequency TFt,j is calculated as
 $${\rm TF}_{t,j} = \displaystyle{{{\rm NT}\lpar {\; T_{\rm C}^{\,t}\comma \; C_i^{\,j}} \rpar} \over {\sum \nolimits_{t = 1}^{{\rm Term}\_{\rm number}\lpar T_{\rm C}} \rpar {\rm NT}\lpar T_{\rm C}^{t}\comma \; C_{i}^{j}\rpar}} \quad \lpar {t\comma \; \,j \in N} \rpar,$$
$${\rm TF}_{t,j} = \displaystyle{{{\rm NT}\lpar {\; T_{\rm C}^{\,t}\comma \; C_i^{\,j}} \rpar} \over {\sum \nolimits_{t = 1}^{{\rm Term}\_{\rm number}\lpar T_{\rm C}} \rpar {\rm NT}\lpar T_{\rm C}^{t}\comma \; C_{i}^{j}\rpar}} \quad \lpar {t\comma \; \,j \in N} \rpar,$$
where ![]() ${\rm NT}\lpar {T_{\rm C}^{\,t}\comma \; C_i^{\,j}} \rpar $ is the occurrence of
${\rm NT}\lpar {T_{\rm C}^{\,t}\comma \; C_i^{\,j}} \rpar $ is the occurrence of ![]() ${{T_{\rm C}^{\,t}} }$ in
${{T_{\rm C}^{\,t}} }$ in ![]() ${{C_{i}^{\,j}} }$ and the denominator is the total occurrence of all terms of T C in
${{C_{i}^{\,j}} }$ and the denominator is the total occurrence of all terms of T C in ![]() ${{C_{i}^{\,j}} }$. The inverse FBS knowledge cell frequency is calculated as
${{C_{i}^{\,j}} }$. The inverse FBS knowledge cell frequency is calculated as
 $${\rm IF}{{\rm F}_t} = \log \left( {\displaystyle{{{\rm NF}\lpar {T_{\rm C}^{\,t}} \rpar } \over {{\rm NF}}}} \right) \quad \!\lpar {t \in N} \rpar \comma$$
$${\rm IF}{{\rm F}_t} = \log \left( {\displaystyle{{{\rm NF}\lpar {T_{\rm C}^{\,t}} \rpar } \over {{\rm NF}}}} \right) \quad \!\lpar {t \in N} \rpar \comma$$
where IFFt states inverse FBS knowledge cell frequency of ![]() ${T_{\rm C}^{\,t}}\comma\; {\rm NF}\lpar {T_{\rm C}^{\,t}} \rpar $ is the number of FBS knowledge cells that contains
${T_{\rm C}^{\,t}}\comma\; {\rm NF}\lpar {T_{\rm C}^{\,t}} \rpar $ is the number of FBS knowledge cells that contains ![]() ${T_{\rm C}^{\,t}}$, and NF is the total number of FBS knowledge cells in the FBS knowledge cell library.
${T_{\rm C}^{\,t}}$, and NF is the total number of FBS knowledge cells in the FBS knowledge cell library.
On the basis of comprehensive consideration of term similarity and frequency of occurrence, the global semantic similarity between ![]() ${{F_{\rm R}^{\,i}} }$ and
${{F_{\rm R}^{\,i}} }$ and ![]() ${{C_{i}^{\,j}} }$ is calculated as
${{C_{i}^{\,j}} }$ is calculated as
 $$\eqalign{&{G_{{\rm SS}}}\left( {F_{\rm R}^{\,i} \comma\; C_i^{\,j} } \right) \cr & \!= \sum_{t = 1}^{{{\rm Term\_number}}({{T_{\rm C}}})}\left\{ {{\rm T}{{\rm F}_{t\comma \,j}} \times {\rm IF}{{\rm F}_t}\, {\times} \left[ {\sum_{s = 1}^{{\rm Term\_number}( {{T_{\rm R}}} )} {{\rm Si}} {{\rm m}_{{\rm SS}}}{{\left( {T_{\rm R}^{\,s} \comma\; T_{\rm C}^{\,t} } \right)}_k}} \right]} \right\} \cr & \qquad \left( {i\comma\;j\comma\;k \in N} \right)}.$$
$$\eqalign{&{G_{{\rm SS}}}\left( {F_{\rm R}^{\,i} \comma\; C_i^{\,j} } \right) \cr & \!= \sum_{t = 1}^{{{\rm Term\_number}}({{T_{\rm C}}})}\left\{ {{\rm T}{{\rm F}_{t\comma \,j}} \times {\rm IF}{{\rm F}_t}\, {\times} \left[ {\sum_{s = 1}^{{\rm Term\_number}( {{T_{\rm R}}} )} {{\rm Si}} {{\rm m}_{{\rm SS}}}{{\left( {T_{\rm R}^{\,s} \comma\; T_{\rm C}^{\,t} } \right)}_k}} \right]} \right\} \cr & \qquad \left( {i\comma\;j\comma\;k \in N} \right)}.$$ Assume similarities of each function pair (![]() ${{F_{\rm R}^{\,i}} }$,
${{F_{\rm R}^{\,i}} }$, ![]() ${{T_{\rm C}^{\,j}} }$) have been obtained, similarities are normalized by using Eq. (11) to conduct normalization.
${{T_{\rm C}^{\,j}} }$) have been obtained, similarities are normalized by using Eq. (11) to conduct normalization.
 $${a_{{ij}}} = \displaystyle{{{G_{{\rm SS}}}\lpar {F_{\rm R}^{\,i}\comma\; C_i^{\,j}} \rpar } \over {\displaystyle\sum \nolimits_{\,j = 1}^{{\rm number}\lpar {{C_{{\rm FBS}}}} \rpar } {G_{{\rm SS}}}\lpar {F_{\rm R}^{\,i}\comma\; C_i^{\,j}} \rpar }} \quad \!\lpar {i\comma\; j \in N} \rpar \comma$$
$${a_{{ij}}} = \displaystyle{{{G_{{\rm SS}}}\lpar {F_{\rm R}^{\,i}\comma\; C_i^{\,j}} \rpar } \over {\displaystyle\sum \nolimits_{\,j = 1}^{{\rm number}\lpar {{C_{{\rm FBS}}}} \rpar } {G_{{\rm SS}}}\lpar {F_{\rm R}^{\,i}\comma\; C_i^{\,j}} \rpar }} \quad \!\lpar {i\comma\; j \in N} \rpar \comma$$
where a ij is normalized value of ![]() ${\rm G}_{{\rm SS}}\lpar F_{\rm R}^{,i}$,
${\rm G}_{{\rm SS}}\lpar F_{\rm R}^{,i}$, ![]() $F_{\rm C}^{,j}\rpar$. The final normalized global semantic similarities can be denoted by a similarity matrix
$F_{\rm C}^{,j}\rpar$. The final normalized global semantic similarities can be denoted by a similarity matrix ![]() ${\rm Si}{{\rm m}_{{\rm SS}}}\lpar {{{{\rm \cal S}}_{\rm R}}\comma\;{{{\rm \cal S}}_{\rm C}}} \rpar $.
${\rm Si}{{\rm m}_{{\rm SS}}}\lpar {{{{\rm \cal S}}_{\rm R}}\comma\;{{{\rm \cal S}}_{\rm C}}} \rpar $.
 $${\rm Si}{{\rm m}_{{\rm SS}}}\lpar {{{{\rm \cal S}}_{\rm R}},{{{\rm \cal S}}_{\rm C}}} \rpar = \matrix{ {\quad \matrix{ {C_{{\rm FBS}}^1} & {C_{{\rm FBS}}^2} & {\matrix{ \ldots & {C_{{\rm FBS}}^n} \cr}} \cr}} \cr {\matrix{ {\matrix{ {F_{\rm R}^1} \cr {F_{\rm R}^2} \cr}} \cr \ldots \cr {F_{\rm R}^m} \cr} \left[ {\matrix{ {\matrix{ {{a_{11}}} & {{a_{12}}} & {\matrix{ \ldots & {{a_{1n}}} \cr}} \cr}} \cr {\matrix{ {{a_{21}}} & {{a_{22}}} & {\matrix{ \ldots & {{a_{2n}}} \cr}} \cr \ldots & \ldots & {\matrix{ \ldots & \ldots \cr}} \cr {{a_{m1}}} & {{a_{m2}}} & {\matrix{ \ldots & {{a_{mn}}} \cr}} \cr}} \cr}} \right]} \cr}.$$
$${\rm Si}{{\rm m}_{{\rm SS}}}\lpar {{{{\rm \cal S}}_{\rm R}},{{{\rm \cal S}}_{\rm C}}} \rpar = \matrix{ {\quad \matrix{ {C_{{\rm FBS}}^1} & {C_{{\rm FBS}}^2} & {\matrix{ \ldots & {C_{{\rm FBS}}^n} \cr}} \cr}} \cr {\matrix{ {\matrix{ {F_{\rm R}^1} \cr {F_{\rm R}^2} \cr}} \cr \ldots \cr {F_{\rm R}^m} \cr} \left[ {\matrix{ {\matrix{ {{a_{11}}} & {{a_{12}}} & {\matrix{ \ldots & {{a_{1n}}} \cr}} \cr}} \cr {\matrix{ {{a_{21}}} & {{a_{22}}} & {\matrix{ \ldots & {{a_{2n}}} \cr}} \cr \ldots & \ldots & {\matrix{ \ldots & \ldots \cr}} \cr {{a_{m1}}} & {{a_{m2}}} & {\matrix{ \ldots & {{a_{mn}}} \cr}} \cr}} \cr}} \right]} \cr}.$$3.3.3. Similarity measures for crisp/interval values
Crisp values and interval values are delimited by sharp boundaries. There are four occasions when computing crisp/interval numeric similarity between required functions and FBS knowledge cells: similarity calculation for crisp-crisp, crisp-interval, and interval-crisp and interval-interval values.
Similarity measure for crisp-crisp values
Similarity between crisp values can be calculated by implementing a one-dimensional Euclidian distance function. Denote x and y as crisp values of the same attribute from the required function and FBS knowledge cell, respectively. The similarity ![]() ${\rm Sim}_{{\rm CN}}^{\rm CC} \lpar x $,
${\rm Sim}_{{\rm CN}}^{\rm CC} \lpar x $, ![]() $ y \rpar_{k}^{i}$ of the ith compared attribute values pair of the kth compared functions pair is as follows:
$ y \rpar_{k}^{i}$ of the ith compared attribute values pair of the kth compared functions pair is as follows:
Similarity measure for crisp-interval values
Given x and [y 1, y 2] as the crisp value of the required function and the interval value the same attribute of the FBS knowledge cell, respectively, the similarity measure is defined as
where ![]() ${\rm Sim}_{{\rm CN}}^{\rm CI} \lpar x$,
${\rm Sim}_{{\rm CN}}^{\rm CI} \lpar x$, ![]() $ y \rpar_k^i $ represents similarity of the ith attribute values pair of the kth compared functions pair.
$ y \rpar_k^i $ represents similarity of the ith attribute values pair of the kth compared functions pair.
Similarity measure for interval-crisp values
Let [x 1, x 2] be the interval value of the required function and y be the crisp value of the same attribute of FBS knowledge, the similarity measure can be defined as
 $$\eqalign{{\rm Sim}_{{\rm CN}}^{{\rm IC}} \lpar {x\comma\; y} \rpar _k^i & = {\rm Sim}_{{\rm CN}}^{{\rm IC}} {\lpar {[ {{x_1}\comma\;{x_2}} ] \comma\; y} \rpar _k} = \displaystyle{{\mathop \int \nolimits_{{x_1}}^{{x_2}} {\rm Sim}\lpar {x\comma\; y} \rpar dx} \over {{x_2} - {x_1}}} \cr & = 1 - \displaystyle{1 \over {{x_2} - {x_1}}}\mathop \int \nolimits_{{x_1}}^{{x_2}} \displaystyle{{\vert {x - y} \vert } \over {{\rm max}\lpar {x\comma\; y} \rpar }}dx\comma\;} $$
$$\eqalign{{\rm Sim}_{{\rm CN}}^{{\rm IC}} \lpar {x\comma\; y} \rpar _k^i & = {\rm Sim}_{{\rm CN}}^{{\rm IC}} {\lpar {[ {{x_1}\comma\;{x_2}} ] \comma\; y} \rpar _k} = \displaystyle{{\mathop \int \nolimits_{{x_1}}^{{x_2}} {\rm Sim}\lpar {x\comma\; y} \rpar dx} \over {{x_2} - {x_1}}} \cr & = 1 - \displaystyle{1 \over {{x_2} - {x_1}}}\mathop \int \nolimits_{{x_1}}^{{x_2}} \displaystyle{{\vert {x - y} \vert } \over {{\rm max}\lpar {x\comma\; y} \rpar }}dx\comma\;} $$
where ![]() ${\rm Sim}_{CN}^{IC} \lpar x $,
${\rm Sim}_{CN}^{IC} \lpar x $, ![]() $ y \rpar_k^i $ represents similarity of the ith attributes value pair of the kth compared functions pair.
$ y \rpar_k^i $ represents similarity of the ith attributes value pair of the kth compared functions pair.
Similarity measure for interval-interval value
If [x 1, x 2] is the interval value of the required function and [y 1, y 2] is the interval value of the same attribute of FBS knowledge cell, the similarity measure should be
 $$\eqalign{{\rm Sim}_{{\rm CN}}^{{\rm II}} \lpar {x\comma\; y} \rpar _k^i & = {\rm Sim}_{{\rm CN}}^{{\rm II}} {\lpar {[ {{x_1}\comma\; {x_2}} ] \comma\;[ {{y_1}\comma\; {y_2}} ] } \rpar _k} \cr & = {{\displaystyle\int \nolimits_{{x_1}}^{{x_2}} \mathop \int \nolimits_{{y_1}}^{{y_2}} \left( {1 - \displaystyle{{\vert {y - x} \vert } \over {{\rm max}\lpar {x\comma\; y} \rpar }}} \right)dydx} \over {\lpar {{x_2} - {x_1}} \rpar \lpar {{y_2} - {y_1}} \rpar }}\comma} $$
$$\eqalign{{\rm Sim}_{{\rm CN}}^{{\rm II}} \lpar {x\comma\; y} \rpar _k^i & = {\rm Sim}_{{\rm CN}}^{{\rm II}} {\lpar {[ {{x_1}\comma\; {x_2}} ] \comma\;[ {{y_1}\comma\; {y_2}} ] } \rpar _k} \cr & = {{\displaystyle\int \nolimits_{{x_1}}^{{x_2}} \mathop \int \nolimits_{{y_1}}^{{y_2}} \left( {1 - \displaystyle{{\vert {y - x} \vert } \over {{\rm max}\lpar {x\comma\; y} \rpar }}} \right)dydx} \over {\lpar {{x_2} - {x_1}} \rpar \lpar {{y_2} - {y_1}} \rpar }}\comma} $$
where ![]() ${\rm Sim}_{CN}^{IC} \lpar x $,
${\rm Sim}_{CN}^{IC} \lpar x $, ![]() $y \rpar_k^i $ represents similarity of the ith attributes value pair of the kth compared functions pair.
$y \rpar_k^i $ represents similarity of the ith attributes value pair of the kth compared functions pair.
3.3.4. Similarity measure for fuzzy numeric values
Crisp/interval values neither always exist nor can they be derived for all design requirements because related domain knowledge may not be thoroughly understood. Under many circumstance, fuzzy numeric expressions are given and described by a relation (<, ≤, ≈, ≥, and >) together with a target attribute value, for example, the output pressure of injector ≈12.7 kPa, in which the relation is ≈ and the target attribute value is 12.7. Many membership functions have been proposed to calculate the similarity between fuzzy numeric values. Many membership functions, which define how to map the fuzzy value to degree of membership between 0 and 1, have been proposed to calculate the fuzzy numeric similarity, for example, the triangular membership function (Trimf), the trapezoidal membership function (Tramf), and the Gaussian membership function (Gaussmf). To reduce the burden of calculation, Tramf is adopted to calculate the fuzzy similarity. The membership functions for different relations in fuzzy numeric expressions are given in Table 1, where x is the real value, y or [y 1, y 2] is the target value, and min and max represent the lower and upper bound of the attribute value. Denote the weight of crisp/interval values as β ∈ [0, 1]. The global numeric similarity ![]() ${\rm Si}{{\rm m}_{{\rm NS}}}\lpar {F_{\rm R}^{\,i}\comma\; C_i^{\,j}} \rpar $ between required functions and FBS knowledge cells can be defined as
${\rm Si}{{\rm m}_{{\rm NS}}}\lpar {F_{\rm R}^{\,i}\comma\; C_i^{\,j}} \rpar $ between required functions and FBS knowledge cells can be defined as
 $$\eqalign{&{\rm Si}{{\rm m}_{{\rm NS}}}\lpar {F_{\rm R}^{\,i}\comma\; C_i^{\,j}} \rpar \cr & \quad = {\rm \beta} \times {\rm Si}{{\rm m}_{{\rm CN}}}\lpar {F_{\rm R}^{\,i}\comma\; C_i^{\,j}} \rpar + \lpar {1 - {\rm \beta}} \rpar \times {\rm Si}{{\rm m}_{{\rm FN}}}\lpar {F_{\rm R}^{\,i}\comma\; C_i^{\,j}} \rpar \cr & \quad= {\rm \beta} \times \mathop \sum \limits_{i = 1}^m {\rm Si}{{\rm m}_{{\rm CN}}}\lpar {x\comma\; y} \rpar _k^{\,i} + \lpar {1 - {\rm \beta}} \rpar \times \mathop \sum \limits_{\,j = 1}^n {\rm Si}{{\rm m}_{{\rm FN}}}\lpar {x\comma\; y} \rpar _k^{\,j}\comma \;} $$
$$\eqalign{&{\rm Si}{{\rm m}_{{\rm NS}}}\lpar {F_{\rm R}^{\,i}\comma\; C_i^{\,j}} \rpar \cr & \quad = {\rm \beta} \times {\rm Si}{{\rm m}_{{\rm CN}}}\lpar {F_{\rm R}^{\,i}\comma\; C_i^{\,j}} \rpar + \lpar {1 - {\rm \beta}} \rpar \times {\rm Si}{{\rm m}_{{\rm FN}}}\lpar {F_{\rm R}^{\,i}\comma\; C_i^{\,j}} \rpar \cr & \quad= {\rm \beta} \times \mathop \sum \limits_{i = 1}^m {\rm Si}{{\rm m}_{{\rm CN}}}\lpar {x\comma\; y} \rpar _k^{\,i} + \lpar {1 - {\rm \beta}} \rpar \times \mathop \sum \limits_{\,j = 1}^n {\rm Si}{{\rm m}_{{\rm FN}}}\lpar {x\comma\; y} \rpar _k^{\,j}\comma \;} $$
where ![]() ${\rm Sim}_{\rm CN}\lpar x$,
${\rm Sim}_{\rm CN}\lpar x$, ![]() $ y \rpar_k^{i}$ ∈
$ y \rpar_k^{i}$ ∈ ![]() $ \lcub {\rm Sim}_{\rm CN}^{\rm CC} \lpar x $,
$ \lcub {\rm Sim}_{\rm CN}^{\rm CC} \lpar x $, ![]() $ y \rpar_k^{i}$,
$ y \rpar_k^{i}$, ![]() $ {\rm Sim}_{\rm CN}^{\rm CI} \lpar x $,
$ {\rm Sim}_{\rm CN}^{\rm CI} \lpar x $, ![]() $ y \rpar_k^{i}$,
$ y \rpar_k^{i}$, ![]() ${\rm Sim}_{\rm CN}^{\rm IC}$
${\rm Sim}_{\rm CN}^{\rm IC}$ ![]() $ \lpar x $,
$ \lpar x $, ![]() $ y \rpar_k^{i} $,
$ y \rpar_k^{i} $, ![]() $ {\rm Sim}_{\rm CN}^{\rm II} \lpar x $,
$ {\rm Sim}_{\rm CN}^{\rm II} \lpar x $, ![]() $ y \rpar_k^{i} \rcub $; m is the total number of crisp and interval values appeared;
$ y \rpar_k^{i} \rcub $; m is the total number of crisp and interval values appeared; ![]() $ {\rm Sim}_{\rm FN}\lpar x $,
$ {\rm Sim}_{\rm FN}\lpar x $, ![]() $ y \rpar_k^{j}$ ∈
$ y \rpar_k^{j}$ ∈ ![]() $ \lcub {\rm Sim}_{\rm FN}^{\rm LE} \lpar x $,
$ \lcub {\rm Sim}_{\rm FN}^{\rm LE} \lpar x $, ![]() $ y \rpar_k^{j} $,
$ y \rpar_k^{j} $, ![]() $ {\rm Sim}_{\rm FN}^{{\rm B}/{\rm A}} \lpar x $,
$ {\rm Sim}_{\rm FN}^{{\rm B}/{\rm A}} \lpar x $, ![]() $ y \rpar_k^{j}$,
$ y \rpar_k^{j}$, ![]() $ {\rm Sim}_{\rm FN}^{\rm GE} \lpar x $,
$ {\rm Sim}_{\rm FN}^{\rm GE} \lpar x $, ![]() $ y \rpar_k^{,j} \rcub $; and n is the total number of fuzzy numeric values.
$ y \rpar_k^{,j} \rcub $; and n is the total number of fuzzy numeric values.
Table 1. Membership functions for different relations

Note: The math relations signs in the column heads are less than or equal to, less than, between or about, greater than or equal to, and greater than, respectively.
Suppose numeric similarities of all functions pairs ![]() $\lpar F_{\rm R}^{i}$,
$\lpar F_{\rm R}^{i}$, ![]() $ C_{i}^{j} \rpar $ have been obtained, numeric similarities could be normalized by implementing Eq. (18) to keeps the value between 0 and 1.
$ C_{i}^{j} \rpar $ have been obtained, numeric similarities could be normalized by implementing Eq. (18) to keeps the value between 0 and 1.
 $$b_{ij} = \displaystyle{{{\rm Sim}_{\rm NS}(F_{\rm R}^{i},F_{\rm C}^{j})} \over {\sum \nolimits_{i = 1}^{{\rm number}(F_{\rm R})} \mathop \sum \nolimits_{j = 1}^{{\rm number}(C_{\rm FBS})} {\rm Sim}_{\rm NS}(F_{\rm R}^{i},F_{\rm C}^{j})}},$$
$$b_{ij} = \displaystyle{{{\rm Sim}_{\rm NS}(F_{\rm R}^{i},F_{\rm C}^{j})} \over {\sum \nolimits_{i = 1}^{{\rm number}(F_{\rm R})} \mathop \sum \nolimits_{j = 1}^{{\rm number}(C_{\rm FBS})} {\rm Sim}_{\rm NS}(F_{\rm R}^{i},F_{\rm C}^{j})}},$$
where b ij is the normalized value of ![]() ${\rm Sim}_{\rm NS} \lpar F_{\rm R}^{i}$,
${\rm Sim}_{\rm NS} \lpar F_{\rm R}^{i}$, ![]() $F_{\rm C}^{j}\rpar $. The global numeric similarities between each pairs of compared functions can be given in the form of a similarity matrix
$F_{\rm C}^{j}\rpar $. The global numeric similarities between each pairs of compared functions can be given in the form of a similarity matrix ![]() ${\rm Si}{{\rm m}_{{\rm NS}}}\lpar {{{{\rm \cal N}}_{\rm R}}\comma \ {{{\rm \cal N}}_{\rm C}}} \rpar $.
${\rm Si}{{\rm m}_{{\rm NS}}}\lpar {{{{\rm \cal N}}_{\rm R}}\comma \ {{{\rm \cal N}}_{\rm C}}} \rpar $.
 $${\rm Si}{{\rm m}_{{\rm NS}}}\lpar {{{{\rm \cal N}}_{\rm R}},{{{\rm \cal N}}_{\rm C}}} \rpar = \matrix{ {\quad \matrix{ {C_{{\rm FBS}}^1} & {C_{{\rm FBS}}^2} & {\matrix{ \ldots & {C_{{\rm FBS}}^n} \cr}} \cr}} \cr {\matrix{ {\matrix{ {F_{\rm R}^1} \cr {F_{\rm R}^2} \cr}} \cr \ldots \cr {F_{\rm R}^m} \cr} \left[ {\matrix{ {\matrix{ {{b_{11}}} & {{b_{12}}} & {\matrix{ \ldots & {{b_{1n}}} \cr}} \cr}} \cr {\matrix{ {{b_{21}}} & {{b_{22}}} & {\matrix{ \ldots & {{b_{2n}}} \cr}} \cr \ldots & \ldots & {\matrix{ \ldots & \ldots \cr}} \cr {{b_{m1}}} & {{b_{m2}}} & {\matrix{ \ldots & {{b_{mn}}} \cr}} \cr}} \cr}} \right]} \cr} \;.$$
$${\rm Si}{{\rm m}_{{\rm NS}}}\lpar {{{{\rm \cal N}}_{\rm R}},{{{\rm \cal N}}_{\rm C}}} \rpar = \matrix{ {\quad \matrix{ {C_{{\rm FBS}}^1} & {C_{{\rm FBS}}^2} & {\matrix{ \ldots & {C_{{\rm FBS}}^n} \cr}} \cr}} \cr {\matrix{ {\matrix{ {F_{\rm R}^1} \cr {F_{\rm R}^2} \cr}} \cr \ldots \cr {F_{\rm R}^m} \cr} \left[ {\matrix{ {\matrix{ {{b_{11}}} & {{b_{12}}} & {\matrix{ \ldots & {{b_{1n}}} \cr}} \cr}} \cr {\matrix{ {{b_{21}}} & {{b_{22}}} & {\matrix{ \ldots & {{b_{2n}}} \cr}} \cr \ldots & \ldots & {\matrix{ \ldots & \ldots \cr}} \cr {{b_{m1}}} & {{b_{m2}}} & {\matrix{ \ldots & {{b_{mn}}} \cr}} \cr}} \cr}} \right]} \cr} \;.$$3.3.5. Global similarity measure (GSM)
When the matrix 12 and matrix 19 are obtained, the global similarity can be calculated by using the following equation.
where ![]() ${\rm Si}{{\rm m}_{\rm G}}\lpar {F\comma\; C_{{\rm FBS}}^{\,i}} \rpar $ is the global similarity, α is weight of
${\rm Si}{{\rm m}_{\rm G}}\lpar {F\comma\; C_{{\rm FBS}}^{\,i}} \rpar $ is the global similarity, α is weight of ![]() ${\rm Sim}_{\rm SS}\lpar {\cal S}_{\rm R}$,
${\rm Sim}_{\rm SS}\lpar {\cal S}_{\rm R}$, ![]() ${\cal S}_{\rm C} \rpar $ and α ∈ [0, 1]. Note that the similarity between the decomposed function and its solution is the composite of similarities of its subordinates.
${\cal S}_{\rm C} \rpar $ and α ∈ [0, 1]. Note that the similarity between the decomposed function and its solution is the composite of similarities of its subordinates.
4. IMPLEMENTATION AND CASE STUDY
4.1. Implementation
To implement the proposed approach, an FBS knowledge cell based ICCDS has been developed, in Java language with jar files (prefuse, jena, and jgraph) to support creative conceptual design. The relational database (MySQL™) is used to store the FBS knowledge cell. It facilities design knowledge representation, management, and allows designers to access multidisciplinary knowledge. Moreover, it introduces semantic understanding ability into the FBS knowledge cell retrieval process. The main interface of ICCDS is shown in Figure 6.
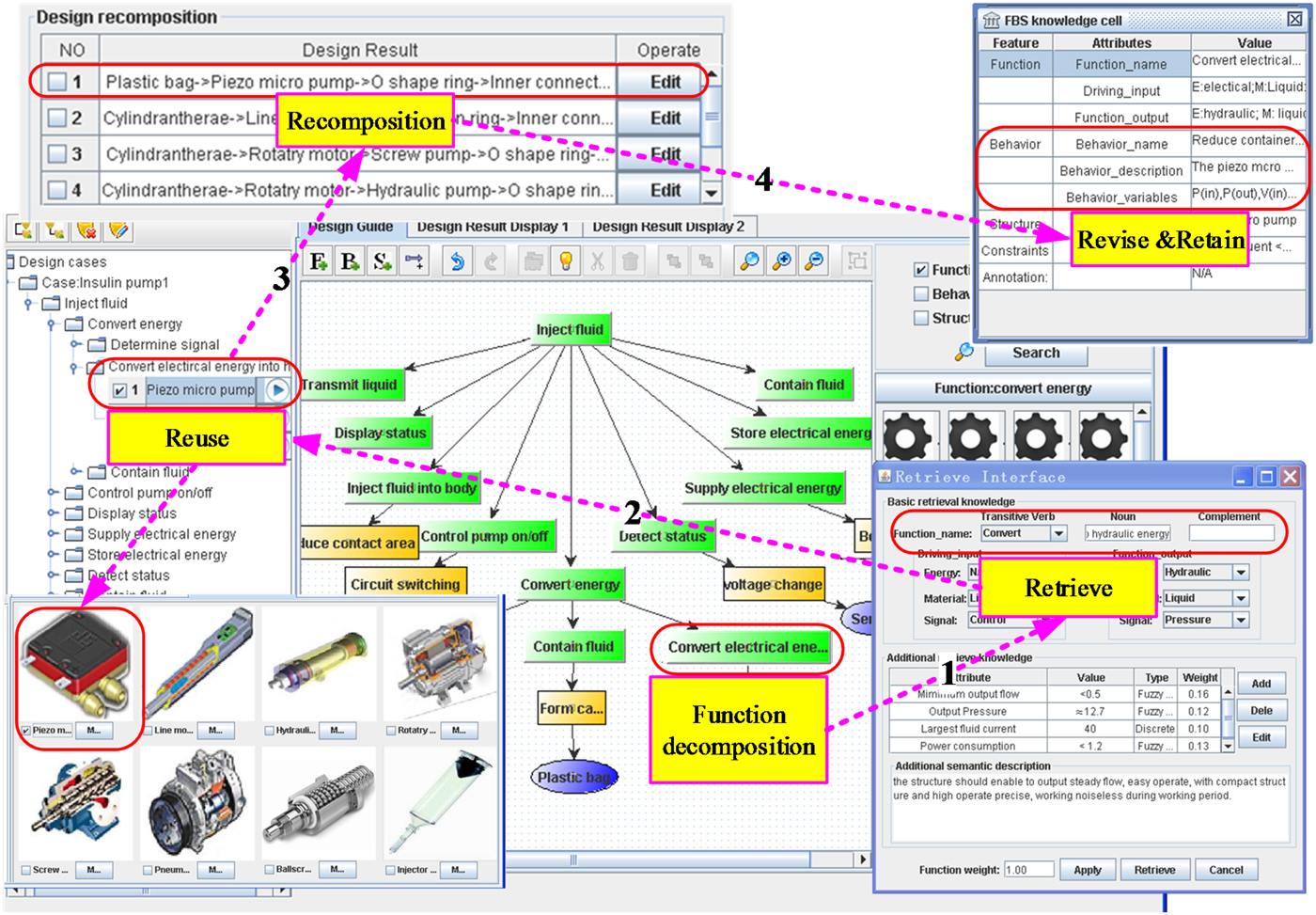
Fig. 6. Interface and demonstration of the developed ICCDS.
As is mentioned above, the FBS knowledge cell library plays a role in function blocks. When confronted with a new design task, it is necessary for designers to extract required functions and decide the basic retrieve knowledge according to the given design requirements. Then specifying the retrieval knowledge to retrieve forth and back between required functions and the FBS knowledge cell library to search for suitable FBS knowledge cells using the proposed hybrid similarity measure, sets of retrieved FBS knowledge cells are added to the corresponding node of the tree-view in the left side of the interface and displayed in tabular form. Designers are allowed to read or adapt design knowledge of each retrieved FBS knowledge cell. FBS knowledge cells in the same tabular node meet the same function, and only one of them is allowed to be chosen to realize its function at every turn. If no suitable FBS knowledge cell is retrieved, the function is decomposed into subfunctions and the retrieval process is repeated. The function decomposition process is displayed in the center of the interface. When all required functions retrieved the satisfied FBS knowledge cells, recompose them through the backtracking function decomposition process and place the FBS knowledge cells end to end to form a design solution chain while ensuring the input flow and the output flow of each FBS knowledge cell are the same with the output flow of the front one and input flow of the back one. Finally, the generated possible design solutions are displayed.
4.2. Illustrative example
An insulin pump makes it possible to accurately deliver insulin and allows for scheduled insulin deliveries of varying amounts at different times of the day for Type 1 diabetes mellitus patients to simulate insulin secretion of the human body. The traditional insulin pump is driven by a high-precision micromotor with the minimum injection dose up to 0.05 U/h. Motivated by proposing better design solutions to improve the performance of the insulin pump through lowering the minimum delivery dose and prolonging the battery life between charges, we attempted to generate some novel design solutions for the insulin pump using our proposed approach. The design process was given as below.
Step 1. Design requirements analysis to extract functions and basic design parameters: Through detailed analysis and discussions of the working mechanisms of a traditional insulin pump, the determined basic functions and the sequential function chain for the flow of the insulin pump were shown as in Figure 7.
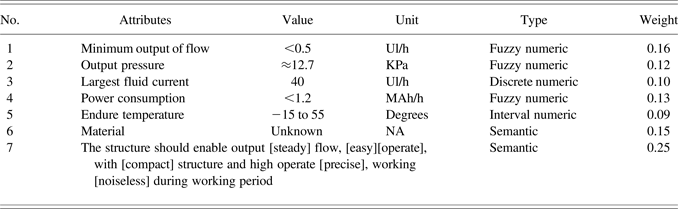
To elaborately demonstrate the retrieval process, one of the most critical functions, Convert electrical energy into hydraulic energy, was taken as an example. The basic retrieval knowledge could be represented as: Function_ name: Convert electrical energy into hydraulic energy; Driving_input: {E: Electrical; M: Liquid; S: Digital}; Function_output: {E: Hydraulic energy; M: Liquid; S: N/A}. The decided additional retrieval knowledge and its weight were given in Table 2, with material unknown to verify the semantic understanding ability of ICCDS. Weights of retrieval knowledge was gotten using the approach of the analytic hierarchy process.
Step 2. FBS knowledge cell retrieval and required function decomposition: Conducting the preselection level to reduce calculation amount according to Section 3.3.1, the preselected FBS knowledge cells and their basic knowledge were given in Figure 8.
It shows that a series of FBS knowledge cells derived from multidisciplinary were retrieved, including electric–mechanical cells (e.g., rotary motor and line motor), mechanic–hydraulic cells (e.g., hydraulic pump and screw pump), electronic–mechanical–hydraulic (e.g., piezo-micro pump), and so on. Specify the given retrieval knowledge into the ICCDS to search for the similar FBS knowledge cells that met the set threshold (θ = 0.7600) and rank them sequentially according to the calculated similarity. However, the value of the attribute Material was difficult for designers without any biomedical background to propose suggestions. Instead of providing professional knowledge, designers could conduct the retrieval process by specifying the relevant term: Medical. The ICCDS would retrieve the FBS knowledge cell library based on WordNet ontology; thus, the FBS knowledge cell contains relevant terms, for example, PVC, PDMS, and POM, and other specified retrieval knowledge would be retrieved. Provided that there was no FBS knowledge cell met the set threshold
 $ {\rm\theta} $, further decompose the function Convert electrical energy into hydraulic energy into Convert electrical energy into mechanical energy and Convert mechanical energy into hydraulic energy, and repeat the retrieval process after determining their basic retrieval knowledge. The retrieved FBS knowledge cells and their retrieval knowledge representation were given in Figure 9.
$ {\rm\theta} $, further decompose the function Convert electrical energy into hydraulic energy into Convert electrical energy into mechanical energy and Convert mechanical energy into hydraulic energy, and repeat the retrieval process after determining their basic retrieval knowledge. The retrieved FBS knowledge cells and their retrieval knowledge representation were given in Figure 9.Step 3. Reuse and recompose: Reuse retrieved FBS knowledge cells by referring to the ranked order of similarity and then remove the unqualified ones. After each function had obtained its suitable FBS knowledge cells, retrieved FBS knowledge cells recomposed to generate suggested design solutions through a backtracking function decomposition process and connecting subfunctions of the same function in chronological order, where output flow of the former FBS knowledge cells were input flow of the latter FBS knowledge cells. The suggested design solutions of the function Convert electrical energy into hydraulic energy were given in Figure 9.
Step 4. Revise: In this step, casual knowledge embedded in the behavior representation of the FBS knowledge cell was used to get a committed design solution. For example, different persons have different skin resistance and need different puncture force to inject insulin into the body, which is difficult to reach for a single piezo micropump (as shown in Fig. 8, the output pressure of piezo micro pump = 6.5 kPa < skin resistance = 12.7 kPa), a revise was stimulated by the attribute Casual_ link of piezo micropump: P out = P in + P produce + P produce (the output pressure is the sum of the output pressure of two single piezo micropumps). The suggested solution was connect two piezo micropumps of two chambers in series, and the connected two piezo micropumps adopts cross working mode: when one piezo micropump absorbs fluid, another piezo micropump drains fluid. Figure 10 demonstrated the revision to solve the problem that the single piezo micro-pump cannot provide sufficient puncture force.
Step 5. Retain: Output design solutions and retain essential design knowledge into database for future design reuse. Analytic hierarchy process could be used as a means to evaluate the performance of the committed design solutions. The accuracy of the injection dose of the improved insulin pump is improved by five times to 0.01 μL, the cost of it is reduced, and the precious battery life is prolonged.
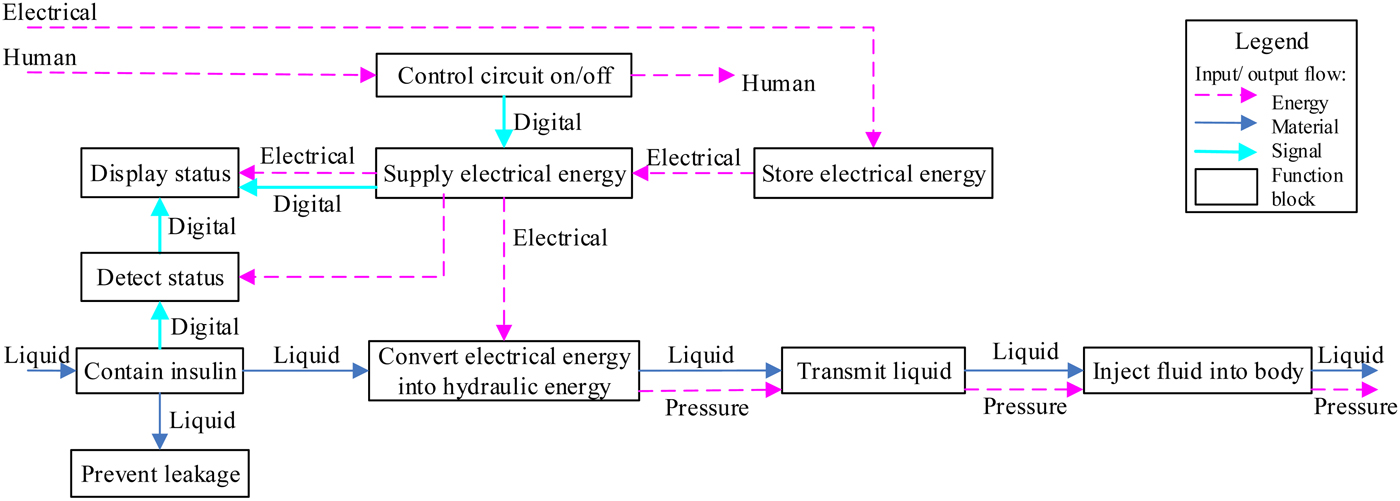
Fig. 7. A sequential function chain for the flow of energy, material and signal of insulin pump.
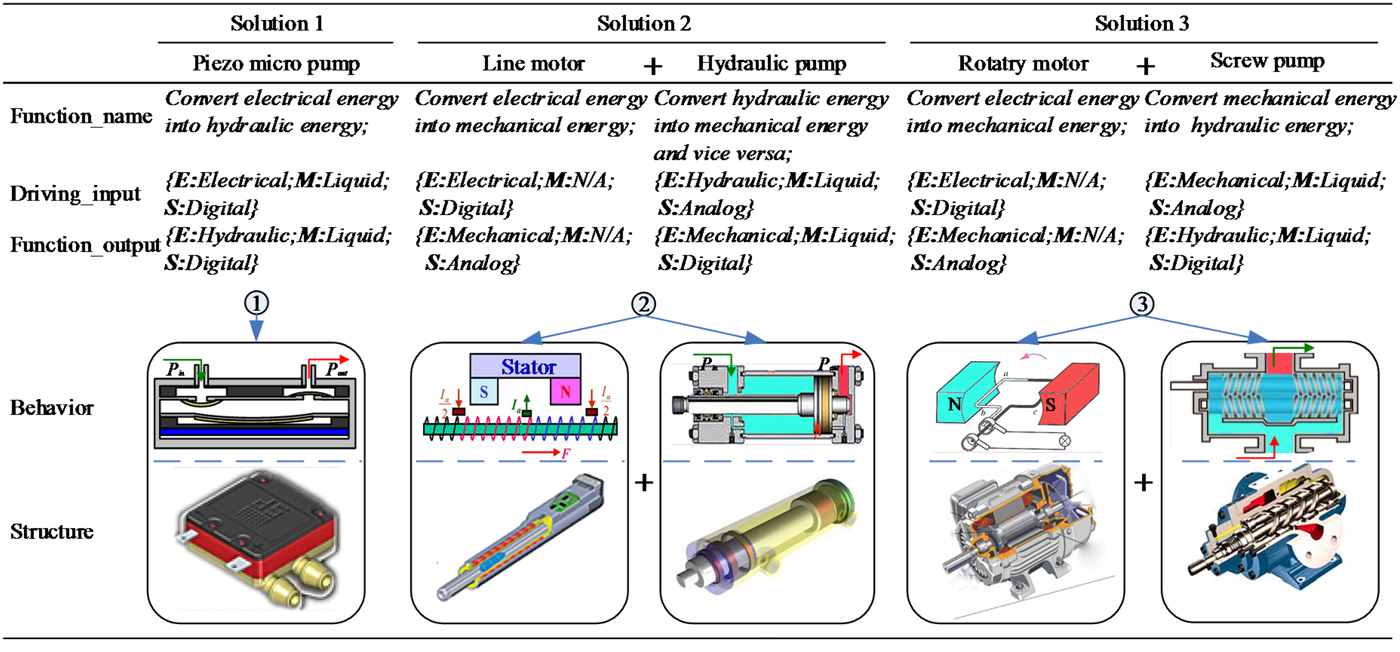
Fig. 8. The preselected FBS knowledge cells and their basic knowledge (partly).
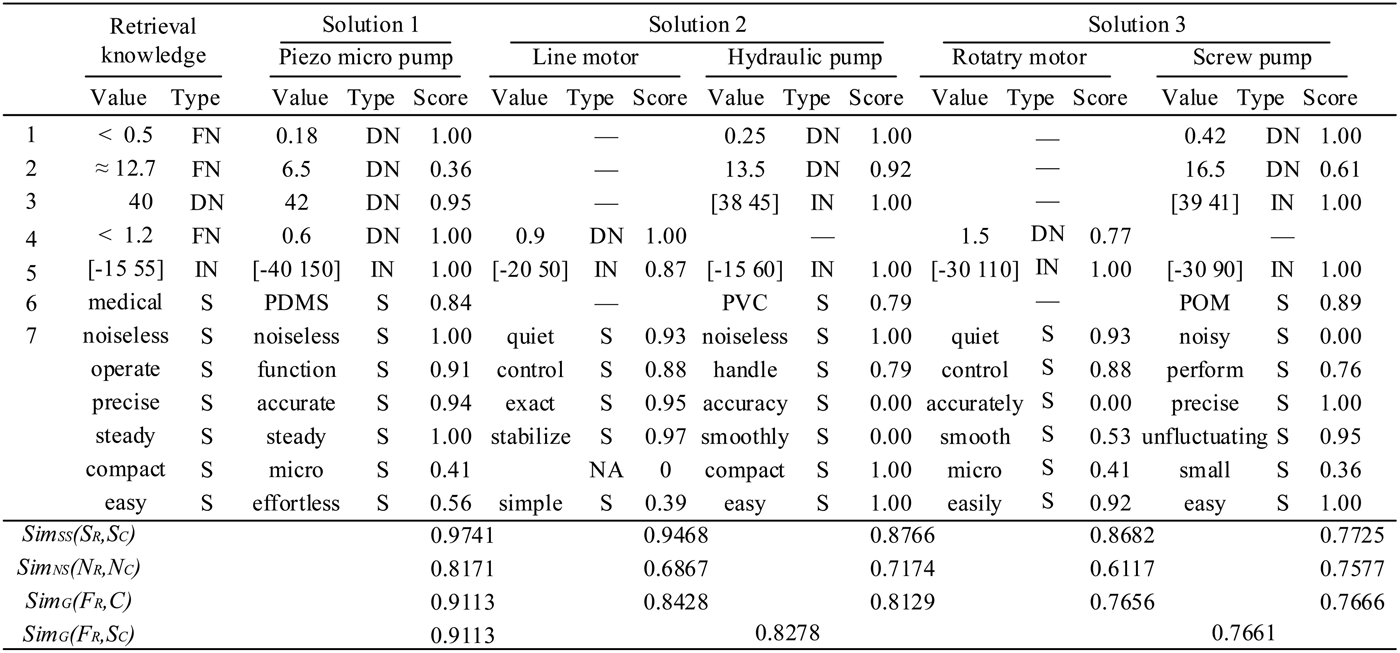
Fig. 9. Comparing FBS knowledge cells with retrieval knowledge of given functions.
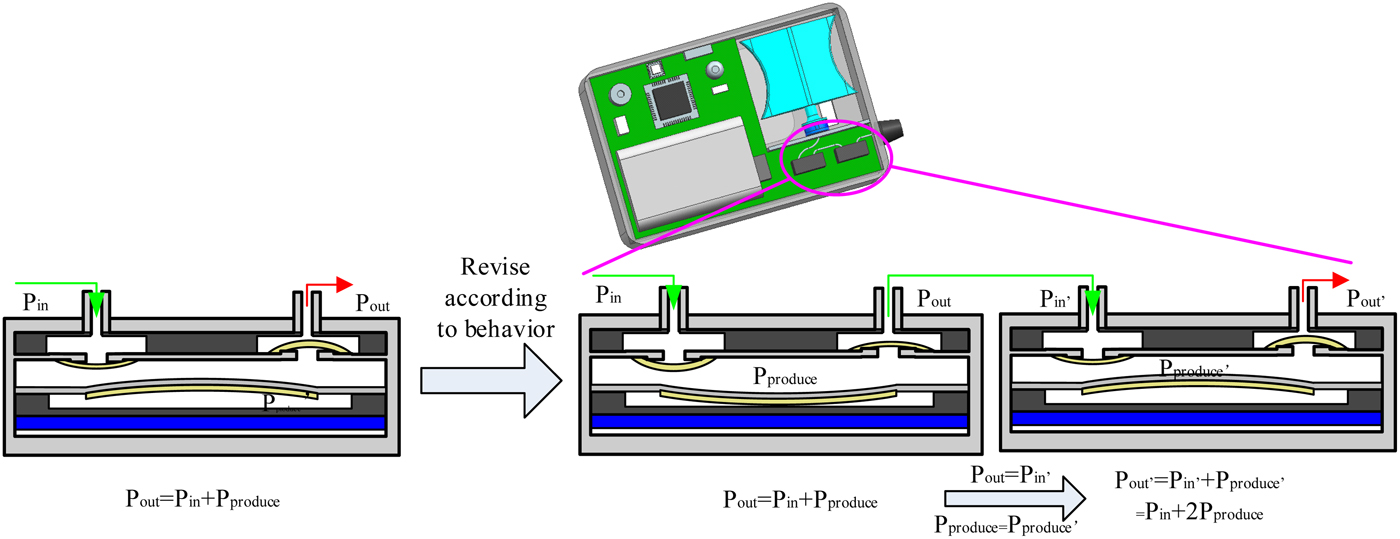
Fig. 10. Revise the design solution to provide sufficient output pressure.
Table 2. The decided additional retrieval knowledge and corresponding weights (α = 0.40, β = 0.32, total weight = 1.00)
4.3. Performance evaluation
To evaluate the performance of the developed ICCDS and the proposed combined approach, 5 graduate students and 10 undergraduate students in the Institute of Knowledge Based Engineering were invited to participate in the experiments with 1189 FBS knowledge cells in the FBS knowledge cell library (obtained from 136 design cases) used as the target function blocks. The participants were selected as subjects because they had creative design related training and some creative design experience, which is necessary for performance evaluation and to ensure the complete concepts recorded. The participants were divided into five groups (G1, G2, G3, G4, and G5), with each group consisting of 1 graduate student and 2 undergraduate students. Nine creative conceptual design tasks (coded 1–9) were adopted to demonstrate the performance of the proposed approach. They were divided into three design levels: the high level with more than two necessary attributes lacking, the medium level with one or two necessary attributes lacking, and the low level with all necessary attributes given clearly. Two experiments were designed to verify the effectiveness of ICCDS. Experiment 1 was conducted to show the effectiveness of the proposed approach in different design levels. Experiment 2 was assigned to improve the reliability of the proposed approach, and a comparative study between the proposed approach and other related approaches was conducted to show how much improvement can be achieved. An expert pane, consisting of 10 famous experts or engineers from five different disciplines (i.e., mechanical engineering, electrical engineering, electronics engineering, hydraulic engineering, and energy engineering) was invited to score the design results using the two indices: novelty (%) and satisfactory (%). They are all experts or engineers with rich conceptual design experience. Novelty is the degree of originality or newness of the generated design solutions. The scores are calculated by the frequency of occurrence of the obtained principles of each of the decomposed subfunctions among the design solutions generated by all the groups (Wilson et al., Reference Wilson, Rosen, Nelson and Yen2010). The more striking or unusual the design solution is, the higher score the group will get. Satisfactory is the degree to which the output design solutions fulfill the design requirement (Guo et al., Reference Guo, Hu and Peng2012). The scores are determined by the design solutions of the decomposed subfunctions.
4.3.1. Experiment 1: A comparative study among different design requirements clarification levels
In this experiment, the performance of ICCDS was summarized taking consideration of the extent of design requirements clarification and the statistic results was shown in Table 3. According to the statistics principle, mean μ(total) and deviation σ(total) were calculated to reflect the distribution of evaluation indexes. From Table 3, we can draw some conclusions. For novelty, the mean μ(total) of novelty ascends from 61.4%, 72.4% to 78.1%, showing that the high-level design activities could generate more striking design solutions because the space of FBS knowledge cells for the designers' choice was compressed and sets of FBS knowledge cells that may stimulate novel design conceptions were eliminated in the retrieval stage. The deviation σ(total) of novelty follows the same trend from 7.3% to 10.9% to 14.3%, revealing that the variation range of novelty of design solutions becomes increasingly larger with the decreasing number of attributes values, presumably because uncertainty and ambiguity of specified design knowledge lead to uncertain design solutions output. For satisfactory, the mean μ(total) of satisfactory of low-level design, medium-level design, and high-level design are 80.1%, 83.2%, and 82.3%, respectively. The low-level design scores are lower than the latter two because it scores relative low in novelty. The high-level design scores lower than the medium one because it consumes more time in retrieve and revise stages. The deviation σ(total)of satisfactory and novelty have the same tendency.
Table 3. Performance comparisons among different design requirements clarification levels
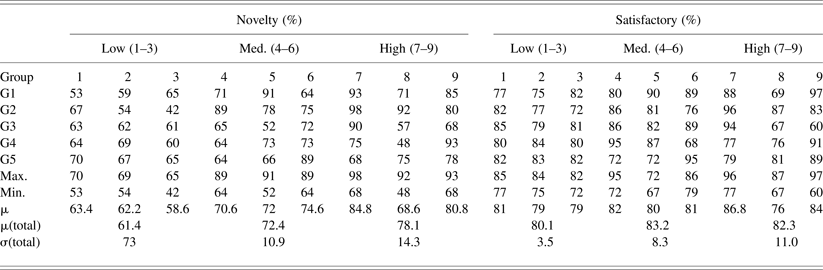
Based on the above analysis, the extent of design requirements clarification had a significant influence on the evaluation indexes. The low-level design has a distinctive advantage in effectively reducing of deviation σ(total). The high-level design performs well in generating striking design solutions but at the expense of the controllability of producing design solutions, for its retrieval performance may be degraded because of missing attribute values are difficult to find. The medium-level design outperforms them in mean μ(total) of satisfactory. There is a trade-off between the extent of design requirements clarification and the quality and number of generated creative design solutions.
4.3.2. Experiment 2: A comparative study between the proposed approach and other approaches
Table 4 presents the comparison of the proposed method and other related methods, for example, traditional CBR (TCBR; Yang & Chen, Reference Yang and Chen2011), multiagent based CBR (MCBR; Epstein et al., Reference Epstein, Yun and Xie2013), genetic algorithm based CBR (GCBR; Yang & Wang, Reference Yang and Wang2008), requirement function behavior principle solutions (Ma et al., Reference Ma, Hu, Zheng and Peng2013), and CFKM based CBR (Hu et al., Reference Hu, Hu, Peng and Cao2012). Table 4 shows that MCBR, GCBR, CFKM and the proposed method perform better than TCBR in all evaluation indexes. GCBR performs better than other models in novelty of low-level design and the average time consumed. The proposed method notably performed better than other models in other indexes except novelty of low-level design and average time consumed. In TCBR, MCBR, and GCBR, while searching for satisfied design cases, the keywords based semantic searching is the most commonly used method, and if the specified keywords are not exactly matching with the design cases in the knowledge database, the retrieval often fails. The proposed method considers numeric expression and semantic description rather than focusing on similarity calculation of one kind of design knowledge or keywords searching. Introduction of WordNet ontology based semantic similarity calculation provides the design process with a semantic understanding ability to extend the design space, and more novel design ideas will be stimulated. Moreover, the proposed hybrid similarity measure improves retrieval accuracy greatly. Thus, in higher level design, the proposed method performs far better than other models.
Table 4. Performance comparisons between the proposed CBR and related models

5. CONCLUSIONS
This paper proposes a combined creative conceptual design approach by integrating the FBS model into the CBR paradigm. It contributes to solving the issues of multidisciplinary knowledge reuse, that is, how to define a reasonable multidisciplinary representation model and how to make the multidisciplinary design knowledge retrieval tractable. For the first issue, the notion of the FBS knowledge cell model, working as function blocks, is proposed to represent design knowledge. Such models are stored and indexed in a database-like library together with a case family for efficient retrieval and reuse. For the second issue, a three-level hybrid similarity measure is presented to increase the overall possibility of retrieving satisfied FBS knowledge cells by considering different types of design knowledge, for example, discrete knowledge, interval knowledge, semantic knowledge, and fuzzy numeric knowledge, and to endow the retrieval process with semantic understanding ability by using WordNet as a reference. An adapted CBR model is presented as the process model to conduct FBS knowledge cells reuse, and an ICCDS has been developed. ICCDS provides the design process with four elements: the FBS knowledge cell library as multidisciplinary knowledge database, a knowledge cells searching tool based on hybrid similarity measure to extend design space, design synthesis based on morphological matrix to generate design solutions, and other creative design methods. Solutions of design requirements are synthesized by combing FBS knowledge cells that are retrieved from the library. The illustrative example demonstrates that the proposed approach and the developed ICCDS can help designers in reusing multidisciplinary design knowledge to stimulate creative thinking and are an important means for generating creative design solutions. Finally, the performance evaluation has shown the high efficiency of the proposed approach. However, even though the proposed method shows very promising results, there is still a lot of work to be carried out in the future. First, the coefficients that appear in our hybrid similarity measure are empirically derived. It is certain that the proposed hybrid similarity measure would be improved further by an optimally designed experiment. Second, different design tasks have different influences on the performance of the proposed method; thus, further effort should be made to separate the influences of different design tasks from different approaches. Third, the developed ICCDS is a prototype system, and it needs continuous improvement, for example, enrich the FBS knowledge cells library and improve the creative design methods.
ACKNOWLEDGMENTS
This research is supported by the National Natural Science Foundation of China (51475288, 51275293), the Innovation Program of Ministry of Science and Technology of China (2015IM010100), and the Shu Guang project supported by Shanghai Municipal Education Commission and Shanghai Education Development Foundation (12SG14).
Jie Hu is a Professor at Shanghai Jiao Tong University. He received his PhD from Zhejiang University, Hangzhou, and conducted his postdoctoral research at Tsinghua University. Dr. Hu leads the National Natural Science Foundation of China under Grants 51075262, 50775140, 50575142, and 60304015. He has developed methods for areas such as concurrent and collaborative design, knowledge fusion, and knowledge-based design. He is interested in concurrent and collaborative design and manufacturing. He has published approximately 100 papers in journals and at conferences.
Jin Ma is a PhD candidate in the Institute of Knowledge-Based Engineering, Mechanical Engineering Department, Shanghai Jiao Tong University. He has participated in research on multidisciplinary creative collaborative design based on knowledge fusion, funded by the National 863 High Technology Research and Development Program of China (2008AA04Z113), and Research on Collaborative Creative Design, funded by National Natural Science Foundation of China (51075262). His current research areas include concurrent and collaborative design and creative conceptual design.
Jinfeng Feng is a PhD candidate in the Institute of Knowledge-Based Engineering at the Mechanical Engineering Department at Shanghai Jiao Tong University. His current research areas of interest include conceptual design and knowledge engineering.
Yinghong Peng is a Professor and Director of the Institute of Knowledge-Based Engineering at Shanghai Jiao Tong University. He received his PhD degree from Central South University, Changsha, and conducted his postdoctoral research at Shanghai Jiao Tong University. Dr. Peng has edited two books and published approximately 100 papers in journals and at conferences.
















