Introduction
The design of complex engineered systems provides a significant challenge to engineering organizations. When designing a complex engineered system with a number of different analyses and concerns, engineers must take into account the many interactions between subsystems in order to optimize the performance of the design. Often this involves coordinating specialists from the relevant disciplines. In the design of a spacecraft, for example, experts in propulsion, computer science, power systems, and many other areas must work together to create a working design (Kroo et al., Reference Kroo, Altus, Braun, Gage and Sobiesky1994). As a result, coordinating these design processes effectively can provide significant increases to the performance of the design organization, increasing the throughput of designs and lowering costs (Smith, Reference Smith1998).
Several frameworks have been used to approach complex engineered systems design, such as integrated concurrent engineering (Smith, Reference Smith1998; Mark, Reference Mark2002), multidisciplinary design optimization (Martins and Lambe, Reference Martins and Lambe2013), and systems engineering (Price et al., Reference Price, Raghunathan and Curran2006). In integrated concurrent engineering, a small team of disciplinary experts, guided by a facilitator, design a complex engineered system over the course of a few 3-hour meetings (Smith, Reference Smith1998; Mark, Reference Mark2002). In multidisciplinary design optimization, an optimization is broken up between disciplines or components to co-optimize different parts of a complex system autonomously (Martins and Lambe, Reference Martins and Lambe2013). In the broader field of systems engineering, different disciplinary areas encompassing all parts or concerns with respect to a design must be brought together to design a functioning system (Price et al., Reference Price, Raghunathan and Curran2006). These approaches rely on delegating the design of different subsystems, components, or disciplinary areas to experts or disciplinary groups, which provides significant challenges to coordinating design activities, as no individual expert is able to comprehensively know how a design change will affect the design as a whole.
The designers (or disciplines, in the case of multidisciplinary design optimization) in each of these organizations are analogous to the agents in a multiagent system in that they act autonomously, but must work together to achieve a desirable design outcome. Additionally, complex engineered systems and the complex systems design process may be represented as networks (Solé et al., Reference Solé, Ferrer-Cancho, Montoya and Valverde2002; Braha et al., Reference Braha, Suh, Eppinger, Caramanis and Frey2006), a typical multiagent systems domain. Multiagent systems have also had success designing policies for other complex systems domains, such as power grids (Dimeas and Hatziargyriou, Reference Dimeas and Hatziargyriou2005; Pipattanasomporn et al., Reference Pipattanasomporn, Feroze and Rahman2009), air traffic control (Agogino and Tumer, Reference Agogino and Tumer2012), and multi-robot coordination (Yliniemi et al., Reference Yliniemi, Agogino and Tumer2014). Consequentially, a multiagent approach has been used as a framework both for designing complex engineered systems (Manion et al., Reference Manion, Soria, Tumer, Hoyle and Tumer2015; Hulse et al., Reference Hulse, Gigous, Tumer, Hoyle and Tumer2017; Soria et al., Reference Soria, Colby, Tumer, Hoyle and Tumer2017) and for modelling design organizations (Jin and Levitt, Reference Jin and Levitt1993; Jin and Levitt, Reference Jin and Levitt1996).
These multiagent models have been used to study negotiation in design settings (Klein et al., Reference Klein, Sayama, Faratin and Bar-Yam2003; Jin and Lu, Reference Jin and Lu2004), mental-model formation in teams (Dionne et al., Reference Dionne, Sayama, Hao and Bush2010; Sayama et al., Reference Sayama, Farrell and Dionne2011), social learning in teams (Singh et al., Reference Singh, Dong and Gero2009), the effect of design problems on optimal team structure (McComb et al., Reference McComb, Cagan and Kotovsky2017), and the effect of designer search behaviors (McComb et al., Reference McComb, Cagan and Kotovsky2015a; Reference McComb, Cagan and Kotovsky2015b). For the purposes of this paper, these models of teams may be placed into two categories: those which represent the full problem to agents and those in which agents act on partial solutions. Those in which agents act on full solutions include the CISAT framework (McComb et al., Reference McComb, Cagan and Kotovsky2015a; Reference McComb, Cagan and Kotovsky2015b), the mental model framework presented in Dionne et al. (Reference Dionne, Sayama, Hao and Bush2010), commonly used optimization methods such as ant (Dorigo et al., Reference Dorigo, Birattari and Stutzle2006) and bee colony optimization (Karaboga and Basturk, Reference Karaboga and Basturk2007), and protocol-based multiagent systems (Landry and Cagan, Reference Landry and Cagan2011). Since these multiagent methods and models of design teams assume that each designer can propose any change in any part of the system, they likely do not represent the coordination challenges present in decomposed, multidisciplinary organizations. As a result, while some studies using these frameworks do produce results showing collaboration improves the design process (Landry and Cagan, Reference Landry and Cagan2011) [which would be expected from engineering research showing that removing barriers to collaboration produces a more effective design process (Smith, Reference Smith1998; Mark, Reference Mark2002)], others do not – instead finding that the best team structures maximize autonomy (McComb et al., Reference McComb, Cagan and Kotovsky2017). It is likely that this is because these models do not account for the ability of designers to exclusively act on a local area of the problem and not the entire design.
Multiagent representations of design in which agents act on partial solutions show more promise towards modeling the effect of collaboration across disciplines on design outcomes, however current work using these models has not approached this specific problem. While early work studied the learning of partial solutions (Moss et al., Reference Moss, Cagan and Kotovsky2004), this model partitioned the roles of agents such that some agents generate solution fragments while others integrate those fragments – essentially coordinating the solution process – making it less representative of coordination problems in a decomposed design process. The model used in Hanna and Cagan (Reference Hanna and Cagan2009) did assign partial solutions to agents, but studied the strategies that emerge in teams as a result of applying an evolutionary process on agents, rather than the effect of collaboration. Additionally, the models presented to study social learning in teams focus on studying the formation of transactional memory and other organizationally desirable behaviors, rather than design outcomes (Singh et al., Reference Singh, Dong and Gero2009; Reference Singh, Dong and Gero2013a, Reference Singh, Dong and Gero2013b). Finally, while models studying negotiating represent the problems inherent in collaborative design well, with agents acting on different subsystems, these models capture a different aspect of collaborative design than is approached in this paper, since in these papers agents are rewarded based on their own part of the design which may or may not be aligned with the overall system objective (Klein et al., Reference Klein, Sayama, Faratin and Bar-Yam2003; Jin and Lu, Reference Jin and Lu2004). In this paper, however, the coordination challenge to model comes not from differing designer objectives, but from the nature of individual designers acting on different parts of the design problem.
Contributions
This work introduces a new multiagent model of design teams specifically targeting complex engineered systems design. This representation allows modeling of independence and collaboration between designers that take into account the core feature of these processes – the decomposition of the ability to design across the topology of the problem. In the multiagent system introduced in this work, this distribution of design agency is represented by having computational designers control different variables of the model which they iteratively propose to optimize the design. Studying behaviors of designers in this model is then used to provide insights into the complex systems design process. The main challenges in developing this model include:
• devising a multiagent learning approach which approximates the collaborative design process by acting as an effective optimization process in which agents act on different variables of the problem
• extending this approach to be compatible with constraints and mixed integer and continuous variables – common features of engineering design problems
• adapting and applying this method to an optimization problem where shared constraints between subsystems must be coordinated
This paper is presented in the following way: ‘Background’ describes the multiagent principles used in this work, and the previous multiagent approaches to design. ‘Application: quadrotor design’ describes the quadrotor design optimization problem used to model a typical multidisciplinary design problem. ‘Multiagent learning for multidisciplinary design’ describes the mechanics of the multiagent optimization method developed in this work. The results section shows and reflects on the effectiveness of using such a method compared with existing optimization approaches and shows the effects of two behaviors – learning and collaboration – on design. Finally, the conclusions section reflects on the insight gained by developing this method and outlines future work in both the method presented in this work.
Background
Developing a multiagent learning-based optimization method requires knowledge of the principles of multiagent learning, optimization, and the problem at hand. This section provides an outline of multiagent systems, multiagent principles which are used in the optimization method, and the previous multiagent approaches in engineering design and optimization.
Multiagent learning
Multiagent systems are systems in which multiple agents autonomously interact with each other and the environment (Stone and Veloso, Reference Stone and Veloso2000; Weiss, Reference Weiss2013). The study of multiagent systems in general covers a broad range of topics such as communication protocols, coordination, and distributed cognition (Weiss, Reference Weiss2013). While a number of architectures exist for designing the cognition of the agents, such as belief-desire-intention, logic-based architectures, and layered architectures, this work relies on the multiagent learning architecture, in which agents use feedback from the environment in terms of rewards to determine which actions to take in a given state. Each of these processes is outlined in the following sections.
Reinforcement learning
Reinforcement learning is a method of predicting or determining the value of actions in an uncertain or stochastic environment based on the previous rewards returned for those actions. It is popularly known for its use in the multi-armed bandit problem (Sutton and Barto, Reference Sutton and Barto1998), in which a gambler hopes to maximize his or her returns on a series of slot machines. Reinforcement learning has also been successfully applied to other problems, such as air traffic control (Agogino and Tumer, Reference Agogino and Tumer2012) and stock price prediction (Lee, Reference Lee2001) in which it is useful to determine returns over time. The simplest case of reinforcement learning is action-value learning, in which an agent keeps a table of values for its actions, and updates the table at each time step according to:
where V(a) is the learned value of the action, r is the reward given for the action taken, and α is the learning rate, which controls the learning step size. More sophisticated methods of reinforcement learning, such as Q-learning (Watkins and Dayan, Reference Watkins and Dayan1992), encode state information in order to allow the agent to learn the values of its actions in different situations, or states, and comparisons with predictions of future rewards. The Q-learning table assignment is:
where Q(s t, a t) is the value given to the action in the current state, α is a learning rate, r t is the reward at the current state, γ is the preference for future rewards, and max(Q(s t+1, a t+1)) is the best value of the next state reached by taking the current action in the current state.
Action selection
Action selection refers to the way agents take actions based on their learned value in a particular situation. Two common approaches are softmax and epsilon-greedy (Weiss, Reference Weiss2013) action selection. For epsilon-greedy action selection, the agent chooses its most highly valued action with probability 1 − ε and a random action with the probability ε. This random action is taken to keep the values associated with each action up-to-date with the current conditions of the environment. In softmax action selection, the agent chooses actions with probabilities based on their relative values. The probability p that an agent takes an action a is based on a temperature parameter τ and value V(a), as shown in the following equation:
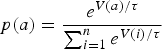 $$p(a) = \displaystyle{{e^{V(a)/\tau}} \over {\mathop \sum \nolimits_{i = 1}^n e^{V(i)/\tau}}} $$
$$p(a) = \displaystyle{{e^{V(a)/\tau}} \over {\mathop \sum \nolimits_{i = 1}^n e^{V(i)/\tau}}} $$where n is the number of actions available to the agent. This temperature parameter τ, which is similar to the temperature parameter used in simulated annealing, acts as a tolerance for sub-optimal values (Richardt et al., Reference Richardt, Karl and Müller1998). For τ → 0 , the agent picks actions greedily, exclusively choosing high-valued actions; for τ → ∞, the actions become equally probable. Softmax action selection is not to be confused with the softmax normalization (also used in this paper), which is used in neural networks to minimize the influence of outliers in a data-set (Priddy and Keller, Reference Priddy and Keller2005).
Reward structure
Reward structure refers to how agents are incentivized based on the results of their actions (Weiss, Reference Weiss2013). When using a local reward, agents are incentivized based on the directly observable results of their actions. When using a global reward, agents are incentivized based on the total result of the actions of all of the agents. When using a difference reward, agents are rewarded based on their individual contribution to global reward. This is calculated by finding the difference between the current global reward, and a hypothetical world in which the agent took a different “counterfactual” action (Agogino and Tumer, Reference Agogino and Tumer2012; Yliniemi et al., Reference Yliniemi, Agogino and Tumer2014). These rewards have attributes that affect the performance of the system as a whole – local rewards are typically most learnable, global rewards are most aligned with the global behavior, and difference rewards capture the good attributes of both (Agogino and Tumer, Reference Agogino and Tumer2008).
Multiagent approaches in engineering design
Multiagent systems have been applied to engineering design problems in a variety of forms, as optimization methods, real and proposed frameworks for design, computational synthesis systems, models of design organizations, and in previous research. These applications are summarized below.
Multiagent optimization methods
A variety of optimization methods have been developed in the past using a multiagent paradigm, including particle swarm optimization, ant colony optimization, and bee colony optimization. In particle swarm optimization, candidate solutions travel through the design space based on information about their own best design and the best design found by all of the agents (Kennedy, Reference Kennedy, Sammut and Webb2011). In ant colony optimization, ants leave “pheromones” communicating the fitness of each solution found and stochastically follow previous trails based on the strength of pheromone (Dorigo et al., Reference Dorigo, Birattari and Stutzle2006). In bee colony optimization, bees communicate the fitness of their route to the next population of bees, which stochastically follow new routes based on the communicated fitness (Karaboga and Basturk, Reference Karaboga and Basturk2007). In each of these optimization methods, agents control candidate solutions rather than design parameters. As a result, these optimization methods are not as analogous to the complex systems design problem as the method presented in this work, making them unfit (as with the models referenced in the introduction) to model decomposition in complex system design, where the agency is instead distributed by components and disciplines.
Multiagent design systems
A variety of multiagent approaches to design have been proposed and applied to perform a variety of design roles. Some multiagent design systems have been proposed to manage the design process, including information flow and design conflicts to enable collaboration or support design activities (Lander, Reference Lander1997). Multiagent design systems have also been applied as computational design synthesis, with agents given different operations to perform on the design, such instantiation, modification, and management (Campbell et al., Reference Campbell, Cagan and Kotovsky1999; Chen et al., Reference Chen, Liu and Xie2014). Finally, multiagent systems have been used to model the engineering design process (Jin and Levitt, Reference Jin and Levitt1993; Jin and Levitt, Reference Jin and Levitt1996; Reza Danesh and Jin, Reference Reza Danesh and Jin2001) and support engineering design (Jin and Lu, Reference Jin and Lu1998; Jin and Lu, Reference Jin and Lu2004). While these systems typically use rule-based agent architectures and not multiagent learning, learning has been proposed as a possible way for agents to discover how their internal conditions affect external conditions (Grecu and Brown, Reference Grecu, Brown, Finger, Tomiyama and Mäntylä2000).
Previous work
Previous work by the authors using multiagent systems to design complex engineered systems involved applying a coevolutionary algorithm to racecar design (Soria et al., Reference Soria, Colby, Tumer, Hoyle and Tumer2017) and applying multiagent learning to the design of a self-replicating robotic manufacturing factory (Manion et al., Reference Manion, Soria, Tumer, Hoyle and Tumer2015). For the racecar application, agents designed sets of component solutions, which were combined into designs. The best performing racecar was selected, and the contribution of each agent was judged by comparing those components with counterfactual components – an adaptation of the difference reward. The team of agents was shown to generate designs which perform better with respect to a set of objectives as designs generated by a real design team. For the self-replicating factory application, each agent was a robot, with roles defining which agents could perform which operations, such as mining regolith or installing solar cells. It was shown that using Q-learning to find the best policies for the agents created a factory which remained productive over the long term, unlike preprogrammed behavior, which was unable to sustain productivity.
While these approaches demonstrated the general applicability of multiagent systems to engineering design, they do not address the problems approached in this paper with respect to problem representation. In the self-replicating factory application, the problem was more focused on designing the policies of the robots that made up the factory than the factory itself. This problem was more comparable to problems commonly encountered in multiagent systems than engineering design since the design solution was a control policy, rather than a set of optimal design parameters. In the racecar application, the problem at hand was very much an engineering design problem, but the brunt of the optimization problem was not handled by the agents themselves, but the cooperative coevolution coordination algorithm. That is, agents in this approach merely represented individual design solutions for each component which were then externally optimized, not the designers of each component which work together to produce an optimal design. The research presented in this paper, on the other hand, is interested in using the agents themselves as the optimization mechanism, rather than an external algorithm, since that is more analogous to complex engineered systems design teams, where the “agents,” or designers, design or optimize based on their own actions, rather than an external algorithm acting on them.
Finally, work by the authors has been shown already towards developing the method presented in this paper using a distributed agent-based optimization method to optimize a quadrotor. This work used an agent-based approach as an optimization method, resulting in the learning assignment used in this work, but without the theoretical justification shown in the section ‘Learning design merit in distributed design’. Additionally, it used an external entity – annealing – to control exploration and exploitation (Hulse et al., Reference Hulse, Gigous, Tumer, Hoyle and Tumer2017), which is tested against other methods of control in the section ‘Meta-agents for multiagent design’. This paper further expands on that paper by extending the case study to a more comprehensive formulation which takes into account more components and operational characteristics, extending the multiagent-based optimization method to act on mixed integer-continuous domains and more explicitly take constraints into account, and using the method as a model to study design teams.
Application: quadrotor design
The method presented in this paper is used to model design teams in conjunction with a quadrotor design problem. This problem was chosen because it embodies the core attributes of a complex engineered systems design problem: constraints which represent the interactions between subsystems and the various requirements which must be met by those interactions. Additionally, as a constrained integer-continuous problem, it provides a significant challenge for our method, as some variables must be acted on differently – while some variables may accept small changes which are not very coupled with others (such as the twist or taper of the propeller), others are highly coupled with each other, and require an optimal configuration (such as the number of batteries to use in series or parallel). It should be stated that problems with inter-disciplinary constraints create considerable challenge towards a decomposed learning-based optimization (as is discussed in the section ‘Learning design merit in distributed design’), since violations of those constraints (for example, caused by an agent choosing a random variable value) necessarily yield extremely bad design outcomes and objective function values. Nevertheless, they are required to properly represent the type of multidisciplinary design that this paper studies, as designers in multidisciplinary design teams must necessarily ensure that their subsystem designs are compatible.
The basic synopsis of the design problem is as follows [a full description is shown in (Hulse, Reference Hulse2017)]. The quadrotor is commissioned to perform ten missions in which it must climb to a height, fly towards, and hover around a number of points of interest, and then descend to its point of origin, visiting the maximum number of points-of-interest possible with its available energy. The objective of the design is to maximize profit based on the revenue of these missions (generated by viewing points of interest) and the cost of the quadrotor. This single-objective approach to an otherwise multiobjective problem (e.g. with mass, cost, and other performances as objectives) is inspired by decision-based design, in which a multi-attribute design problem is transformed into a single-attribute design problem of maximizing profit by using a demand model (Chen and Wassenaar, Reference Chen and Wassenaar2003) – instead of weighting the various objectives, the importance of each objective is modeled based on the value generated. The variables and constraints of the problem are shown in Tables 1 and 2, respectively. Since the mission has a number of operational characteristics (hovering, climbing, and steady flight), these constraints are considered for each characteristic. Note that for our purposes the model is considered a black box, with all equality constraints (as well as an external model) considered a part of the objective rather than a constraint given to the optimizer. This multidiscipline-feasible optimization framework was used because the coupling variables of each subsystem have a higher dimensionality than the subsystem design variables [making it a preferred framework (Allison et al., Reference Allison, Kokkolaras and Papalambros2009)], and because this research is studying the coordination of designers – not the model structure. Additionally, this structure makes the one-variable-per-agent multiagent system a more realistic model of design, since the impact of each design variable is large and in several cases (such as the motor or battery cell) directly sets several other parameters of the design. The full description of these models is shown in (Hulse, Reference Hulse2017), however, for the purposes of this paper it merely provides a multidisciplinary mixed-integer problem domain that encompasses challenges that multidisciplinary teams encounter: inter-disciplinary requirements that cause the optimal selection of a variable of one discipline to be coupled with the variable values in other disciplines.
Table 1. Design choices for each component for the quadrotor design application
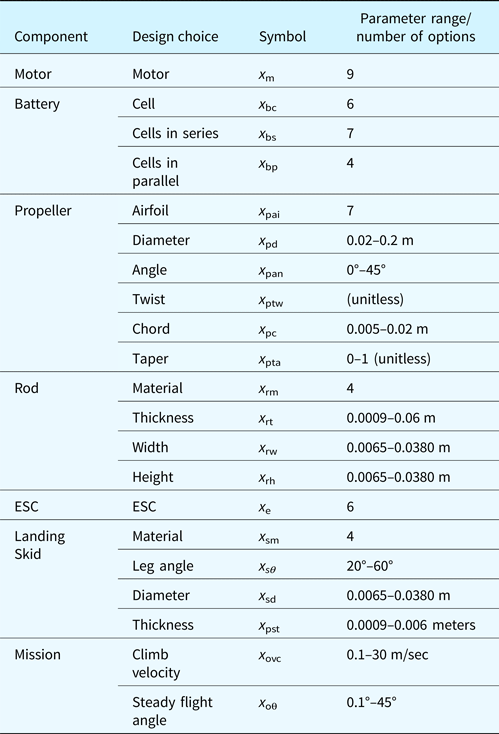
Shown are the components each variable is associated with, the design choice that variable represents, the symbol used by that variable, and the parameter range (for continuous variables) or number of options available (for discrete variables) for that variable.
Table 2. Design constraints for quadrotor design application

Shown are the components the constraints belong to, the equation of the constraint in negative-null form, and an explanation of the constraint.
Multiagent learning for multidisciplinary design
This section presents a multiagent learning-based optimization method which this paper uses to study decomposed, multidisciplinary design. The core representation of learning from the environment when a problem is decomposed between individual designers is presented in the section ‘Learning design merit in distributed design’, along with a game-theoretic justification of the custom learning heuristic presented in this paper. Then the stochastic optimization method based on this representation is presented in the section ‘Multiagent learning-based design optimization method’, along with a summary of important parameters in the section ‘Implementation’.
Learning design merit in distributed design
This method presented in this work is based on a custom learning heuristic specifically designed to represent optimization on a problem which has been decomposed across disciplinary lines to different designers. While multiagent learning systems have been shown to optimize the time-based actions of agents on distributed problem domains, their application to a general design optimization context is hindered because the merit of actions in a design context is highly coupled with the other actions taken. In distributed design, interdisciplinary constraints mean the design of one subsystem and another subsystem have a significant impact on the overall performance of the system.
To understand how this property of distributed design hinders multiagent learning, consider the simple design problem shown in Figure 1 using the notation of game theory with a single reward for both agents. In this problem, each designer must pick a design (A or B) for their subsystem, which, when put together with the other designer's subsystem, has the best performance. While design A–A and B–B are compatible, A–B and B–A are not, such that they fundamentally have no merit as designs. However, while Design B–B has better performance than design A–A, design A–B is less infeasible than design B–A. If the designers traverse the entire space of designs A–A, A–B, B–B, and B–A in four time-steps, the learned value of each design for each designer using the standard reinforcement learning heuristic V(a) ← V(a) + α(r − V(a)) with α = 0.1 is shown in the middle of Figure 1. Based on their learned values, the designers would conclude that design A-B was the best, despite being an infeasible (and third-worst) design. This is because this learning heuristic captures the “average” value of an action, which is overly skewed by infeasible reward values.
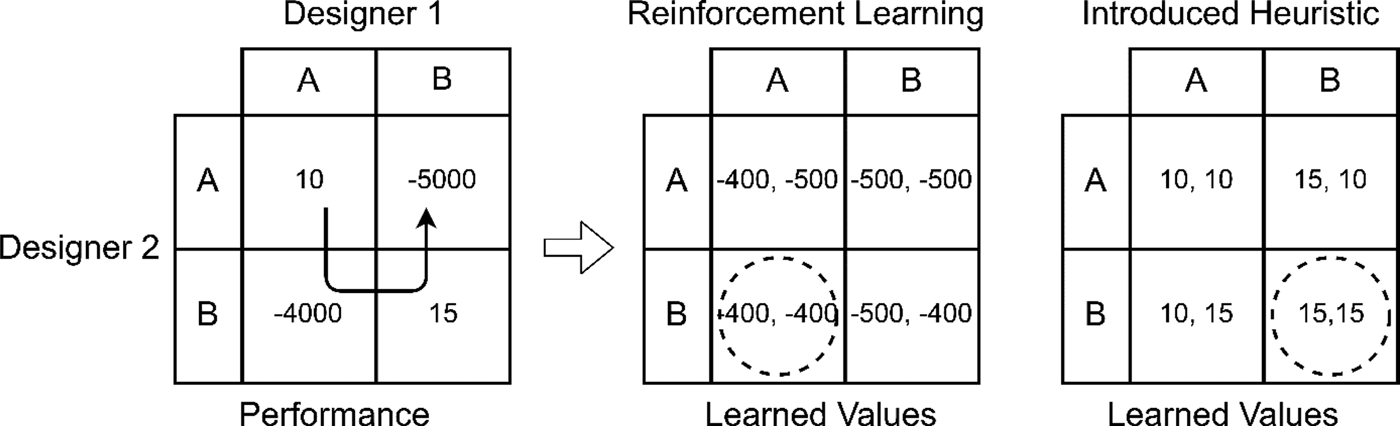
Fig. 1. Learned values of reinforcement learning and this paper's introduced heuristic on a simple example problem meant to capture the coupling between different designer's choices. Each agent has two designs which may be picked – A and B. Traversing the full space of designs, reinforcement learning designers do not encode the optimal design, while designers using the introduced heuristic do.
In the learning heuristic presented in this paper, this problem is solved by having designers simply learn the best value for their action entered so far. This approach can be thought of as a simplification and adaptation of leniency in multiagent learning. With leniency, agents ignore poor individual rewards (which may be due to poorly-matched actions with their team-mates) in order to focus on higher rewards from good joint actions, which helps agents proceed from poor Nash equilibria to optimal Nash equilibria (Panait, Reference Panait, Tuyls and Luke2008). If the designers traverse the entire design space using this heuristic, V(a) ← max(V(a), r), their values for each variable are shown on the right side of Figure 1. As can be seen, while the learned values are inaccurate for the infeasible designs, they are accurate for the feasible designs. Most importantly, the heuristic allows the designers to identify the optimal design, as it has the highest learned values for both designers. It should also be noted that this heuristic does not change values (as would reinforcement learning) depending on how the designers explore the space (e.g. designer 2 choosing design A more than B giving it a lower value over time), but gives a constant value based on the actual performance given so far by the problem. This shows how this introduced heuristic better represents the collaborative design process compared with reinforcement learning.
Multiagent learning-based design optimization method
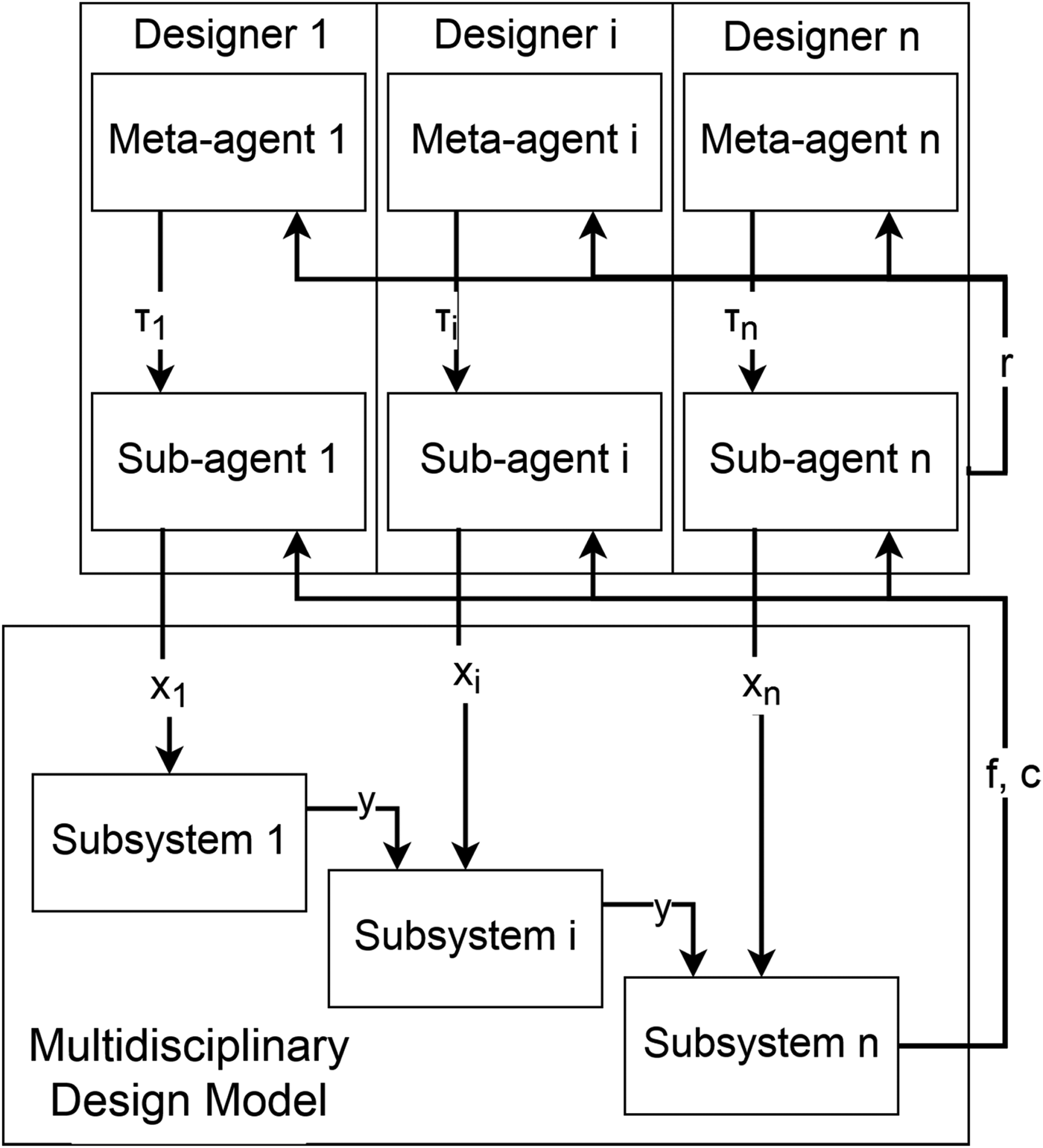
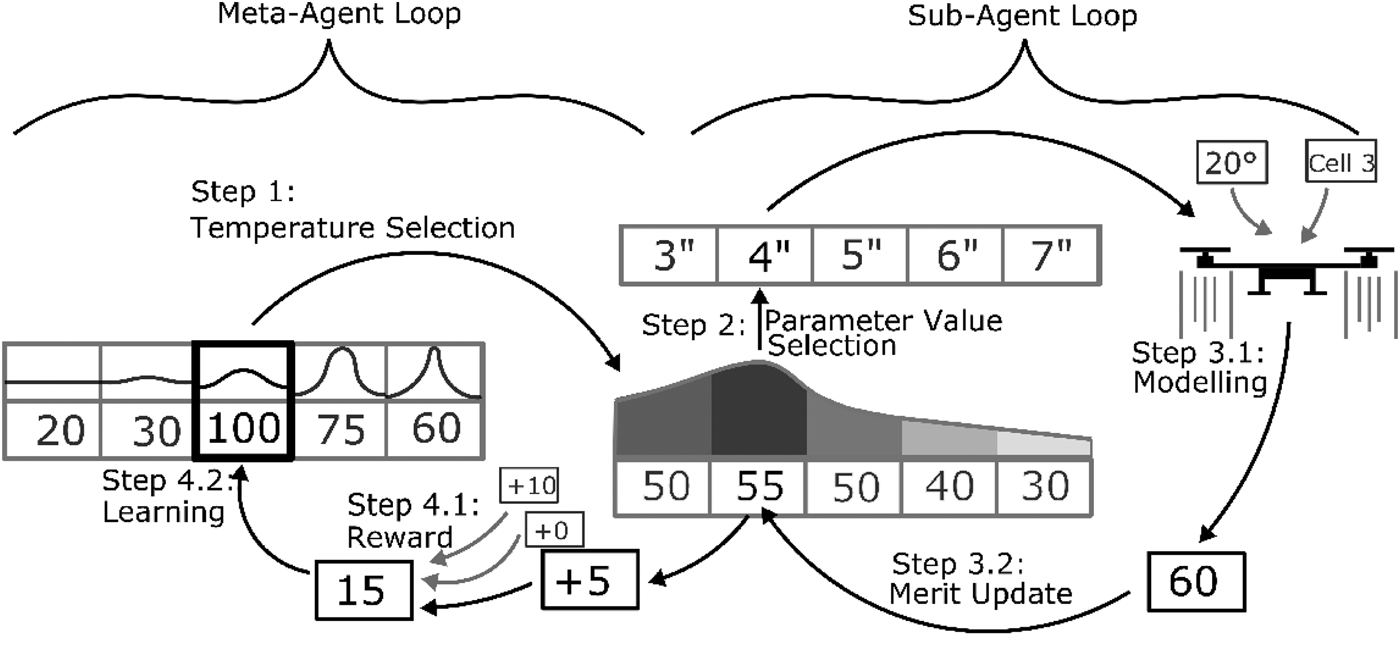
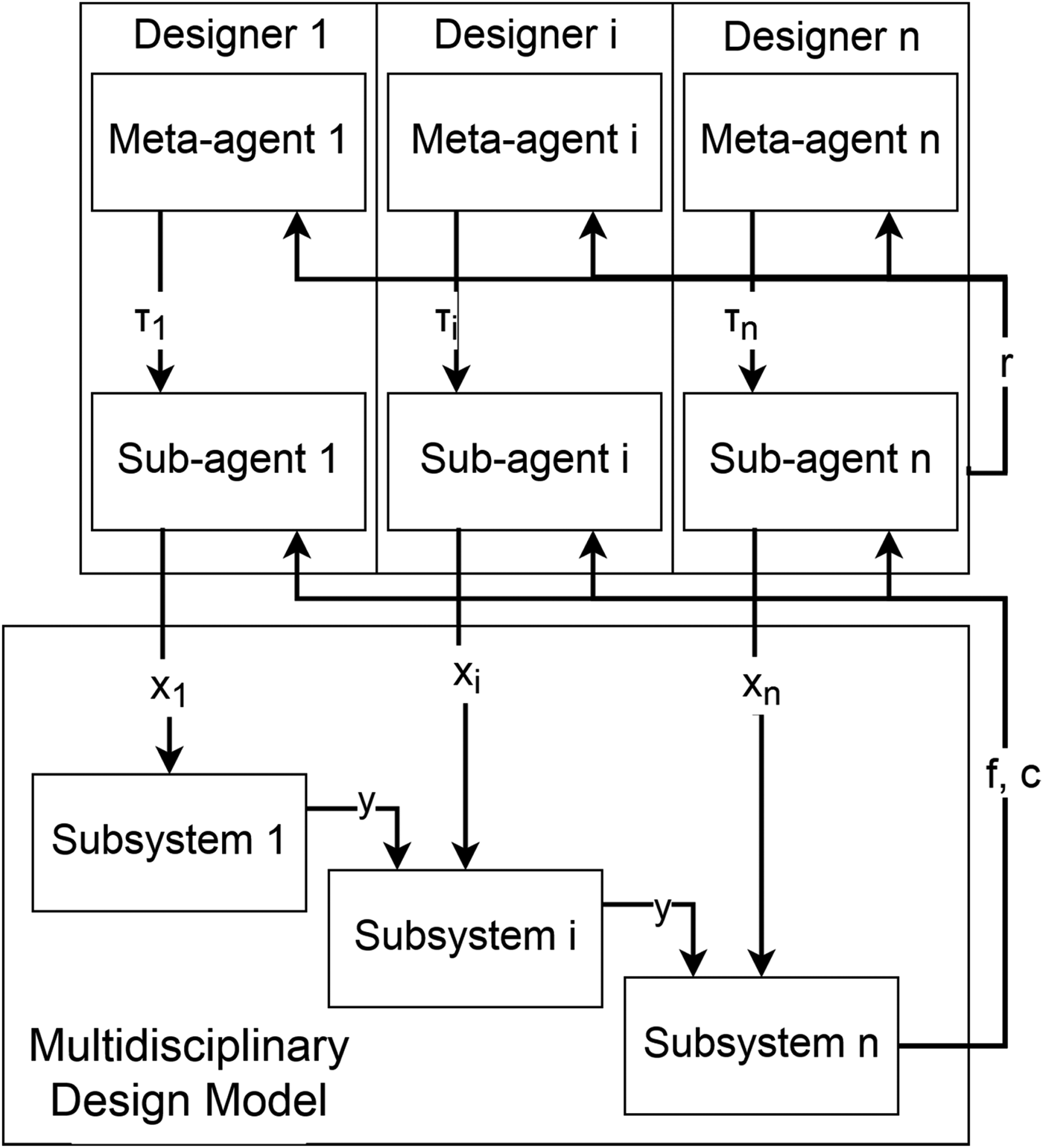
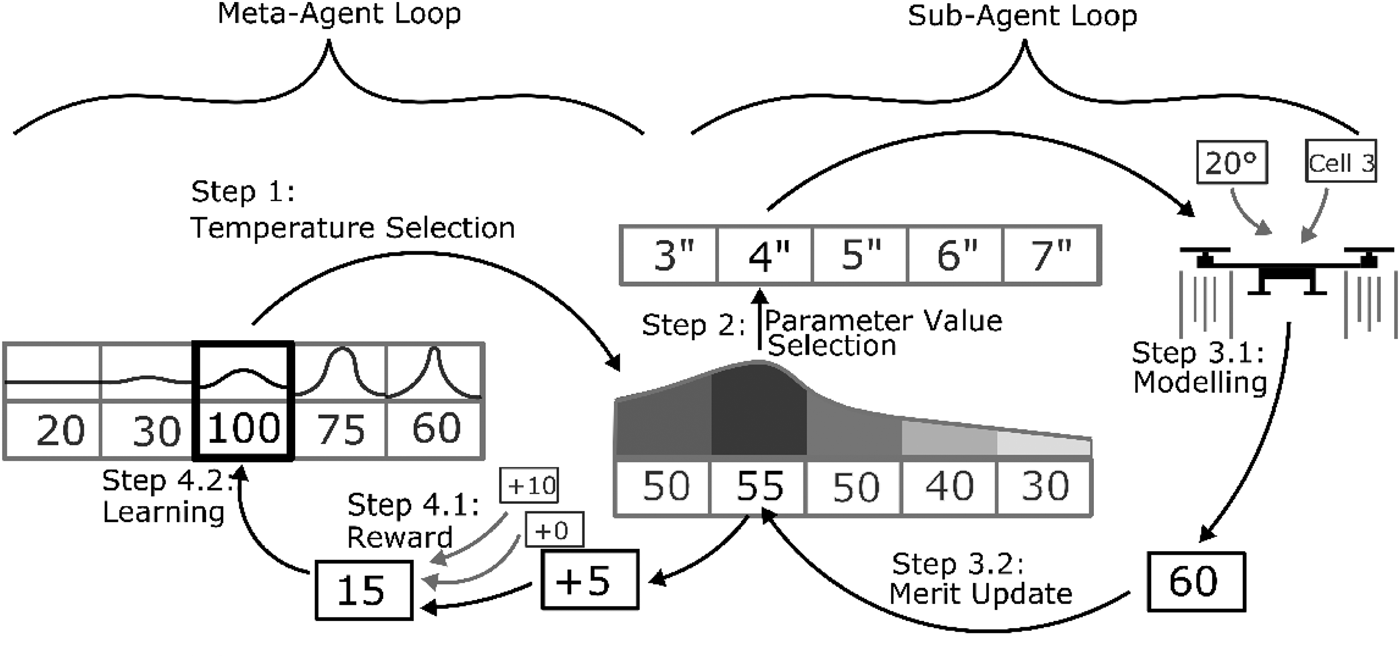
Designers in this framework are best thought of as meta-agents controlling the exploration of sub-agents which in turn pick which variable values to submit to the model at each iteration of the algorithm, as shown in Figure 2. Each computational designer is delegated the design of one variable value in the model and learns two things based on feedback with the environment: which variable values are good (through the sub-agent) and whether to explore new variable values or exploit the current best values (through the meta-agent). The sub-agents use the heuristic introduced in the section ‘Learning design merit in distributed design’, while the meta-agents use stateless reinforcement learning to control the degree of exploration or exploitation of those sub-agents in picking variable values since the required amount of exploration is likely to change throughout the design process. The general steps of the algorithm shown below are illustrated in Figure 3.
Step 1. Meta-Agent Action Selection: Using an epsilon-greedy action selection process, the meta-agents choose the temperature (level of exploration) to use in picking the value of the design variable.

Fig. 2. High-level structure of the multiagent optimization method and design model. Designers consist of meta-agents control sub-agents which pick design parameter and receive rewards based on design performance.

Fig. 3. Overview of method described in the section ‘Multiagent learning-based design optimization method’ shown for a single agent in the multiagent system. The meta-agent chooses a temperature, which the sub-agent uses to compute probabilities of design parameters based on their learned value. After modeling generates objective and constraint values, they return to the sub-agent, which updates the merit according to a heuristic. The new learned values by each of the sub-agents then returns to the meta-agent as a reward to be learned.
Step 2. Sub-Agent Design Parameter Selection: Based on this temperature value and a table listing the merit of each parameter value, the sub-agents choose the parameter values of the design.
Step 3. Sub-Agent Merit Update: The model gives the performance of the resulting design in terms of the objective and overall constraint violation. Per the learning technique introduced in the section ‘Learning design merit in distributed design’, if this performance is better than the performance previously in the table of any agent, the value in that table is updated.
Step 4. Meta-Agent Rewards and Learning: The increase in value in each table is given to the Meta-agent as a reward. Depending on the reward structure, these rewards are added together (global reward) or given individually (local reward) to each agent. The meta-agents learn this reward for their chosen temperature using reinforcement learning.
Steps 1–4 are repeated until a stopping condition is reached. Each step is described in depth in the following sections. Note that the notation for actions and rewards differs from the general notation, with actions and rewards for the sub-agent i stated as x i, and a combination of the objective and constraint values f and c, respectively, while actions and rewards generated by meta-agent i is denoted as τ i, and ![]() $r_{f_i}$, and
$r_{f_i}$, and ![]() $r_{c_i}$, respectively.
$r_{c_i}$, respectively.
Meta-agent action selection
Meta-agents are mechanisms which control the exploration and exploitation level in order to act based on current knowledge or seek new knowledge of the merit of the design variable. They are used to coordinate the sub-agents to find the optimal design parameters quicker by causing sub-agents to explore untried combinations of variable values. This is done by having each meta-agent i choose the temperature τ i based on its value table for a given set of temperatures. The action selection process for meta-agents is epsilon-greedy, as described in the section ‘Action selection’, choosing the best temperature with a certain probability and a random temperature with a certain probability.
Sub-agent design parameter selection
Sub-agents realize the level of exploration or exploitation by using the selected temperature to pick the variable value based on the performance of past designs. This performance is encoded in a table which stores the best previous value of each parameter value in terms of objectives f s(x i) and constraint violation c s(x i). By storing the best previous value of each parameter value, the sub-agents collectively store the best design point found so far, as well as the relative known merit of each design parameter, unbiased by incompatible previous designs. To generate a single metric of merit for the action selection process, these quantities are combined using:
where M(x i) is the combined metric of merit, x i is the variable value i, f s(x i) is the stored objective value, c s(x i) is the stored constraint violation value, and σ is a scaling factor which is similar to penalties used in common constrained optimization methods (Fiacco and McCormick, Reference Fiacco and McCormick1966).
This merit is then normalized using a softmax normalization, putting the variable values with the worst possible merit at 0 and the variable values with the best possible merit at 1. This normalization is used to reduce the influence of outlying stored values on the action selection process, and allows the action selection process to work regardless of the scale it acts on. This normalization follows the equation:
where M(x i)n is the normalized merit, M(x i) is the non-normalized merit, and μ x and σ x are the mean and standard deviation of the merit of the n variable values [x 1…x i…x n ] available to the agent, respectively.
The variable value is then chosen based on the softmax action selection process outlined in the section ‘Action selection’, with the probability of choosing a variable value determined by the equation:
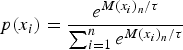 $$p(x_i) = \displaystyle{{e^{M{\lpar {x_i} \rpar }_n/\tau}} \over {\mathop \sum \nolimits_{i = 1}^n e^{M{\lpar {x_i} \rpar }_n/\tau}}}$$
$$p(x_i) = \displaystyle{{e^{M{\lpar {x_i} \rpar }_n/\tau}} \over {\mathop \sum \nolimits_{i = 1}^n e^{M{\lpar {x_i} \rpar }_n/\tau}}}$$where p(x i) is the probability of choosing a variable value x i, M(x i)n is the normalized merit of variable value i, and τ is the temperature. In this framework, this temperature is chosen by the meta-agent as outlined in the section ‘Meta-agent action selection’.
Sub-Agent merit update: design performance
Sub-agents learn the merit of each variable value through interaction with the model using an adaptation of the learning heuristic introduced in the section ‘Learning design merit in distributed design’. After each of the variable values has been chosen by the sub-agents, the design is modeled with each of those variable values, generating an objective function value f and constraint violation value c. This design information is captured by updating the stored value of each variable value f s(x i) or c s(x i) if the found objective and/or constraint violation value is better than the currently stored value, per the learning heuristic introduced in the section ‘Learning design merit in distributed design’, but with further adaptations for determining how values compare with each other given both objective and constraint values. In addition, the reward for the meta-agents is calculated based on this learning process as the difference between the old value and the updated value.
The control logic for this is shown in Algorithm 1. If the found constraint value is better than the stored constraint value, the objective and constraint value is updated, and a reward is calculated for the meta-agent based on the decrease of the constraint value and the objective value if the objective value decreased. If the found constraint value is the same as the stored constraint value, but the objective function is better than the stored objective value, the stored objective value is updated and a reward is calculated. Otherwise, the currently stored merit is kept and a reward of zero is returned for that agent's variable. The result of this adaptation is that feasibility is always considered the primary consideration in saving a design value, followed by performance – no high performance (but ultimately meaningless) design is considered better than a feasible design for the purposes of learning.
Adaptation to continuous variables
This learning process is further adapted to continuous variables by separating continuous space into zones [z 1…z i…z n] represented by the best possible values [f zr1…f zri…f zrn] and [c zr1…c zri…c zrn] at points [x zr1…x zri…x zrn] inside the respective zones. A piecewise cubic hermite polynomial interpolation is then made between each point, creating objective and constraint functions f s and c s for the variable at each value of the variable analogous to the value table used for the discrete variables. The vectors returned by this interpolation x = [x 1…x n], c s = [c x1…c xn], and f s = [f x1…f xn] are then used in the same way as discrete merit tables to pick a variable value. Learning for continuous variables then follows the same process as with discrete variables, except instead of having a better value than the stored value of the current variable value, the found value must be better than the point which represents of the zone. This is, f zri and c zri are used in Algorithm 1 instead of f s and c s. This process is illustrated in Figure 4.

Fig. 4. Visualization of the continuous merit update process described in the section ‘Adaptation to continuous variables’. A spline is fit through the best points found in each zone of the continuous space.
Meta-Agent rewards and learning: improvement over expected values
The rewards for the meta-agents are calculated as the increase in knowledge gained by exploring or exploiting that variable. This reward is calculated from the increases in objective and constraint value ![]() $r_{f_i}$ and
$r_{f_i}$ and ![]() $r_{c_i}$ for each agent/variable i which are calculated as shown in Algorithm 1. The reward r i generated by each agent is then:
$r_{c_i}$ for each agent/variable i which are calculated as shown in Algorithm 1. The reward r i generated by each agent is then:
where σ is a scaling factor which takes the place of a penalty factor.
Two reward structures can be easily constructed based on these rewards: a local reward structure in which meta-agents are rewarded solely on the information gained by their sub-agents, and a global reward in which the meta-agents are rewarded by the sum of the rewards of the sub-agents. In this case it is expected that the global reward should be used, since there are no barriers to calculation and because it better aligns the meta-agents’ actions with the desired purpose of the overall behavior, and achieves better results on common multiagent systems domains (Agogino and Tumer, Reference Agogino and Tumer2008), however, both will be tested in the section ‘Meta-agents for multiagent design’. The local reward L i and global reward G i are calculated for each meta-agent i as:
 $$G_i = \mathop \sum \limits_{i = 1}^n r_i$$
$$G_i = \mathop \sum \limits_{i = 1}^n r_i$$where r i is the reward based on new knowledge generated by each corresponding sub-agent i.
Implementation
When using this method, a few adjustment parameters should be considered. These parameters, as well as a short explanation and the values used in the following tests, are shown in Table 3. Stopping conditions must also be considered, which may be (like other optimization methods) based on the number of function evaluations without improvement, the total number of evaluations, or reaching a desired objective function value. This optimization method would also allow for unique stopping conditions based on learning, such as the number of evaluations without learning or the decrease in the magnitude of rewards over time.
Table 3. Method adjustment parameters, including the symbol they are referred to in the text, an explanation of the symbol, and the value taken
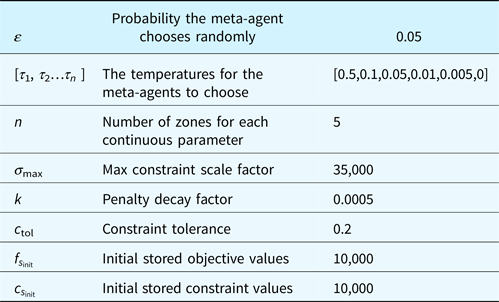
When applying the method to a given problem, the method must also be given a few things in order to initialize and define the agents. For each integer variable, the method must be given the number of available values the variable can take. For each continuous variable, the method must be given the upper and lower bounds of the variable, the number of zones to split that variable into, and the minimum tolerance for the variable at which there is no discernible difference. Additionally, the method must be adapted to the constrained problem through a single metric of feasibility, which in these tests was chosen to be:
 $$c = \mathop \sum \limits_{\,j = 1}^n \hbox{c}_j^2$$
$$c = \mathop \sum \limits_{\,j = 1}^n \hbox{c}_j^2$$where c is the metric of feasibility, m is the number of constraints, and c j is an individual constraint. These constraints have a large impact on the problem, and in practice, it was found that the penalty factor works best when it is increased over time according to:
where e is the current evaluation, k is a decay constant, and σ max is the maximum value of the penalty parameter. This method of combining constraints with the objective used in this paper is similar to what is done in most penalty methods, such as SUMT, in which the penalty is increased over time when the optimization approaches an apparent minimum (Fiacco and McCormick, Reference Fiacco and McCormick1966).
Results
The following tests demonstrate the effectiveness of the multiagent approach presented and then use the approach to study the complex systems design process. This is done in the following sections by:
1. comparing the multiagent method with centralized algorithms in the section ‘Viability of the multiagent design method’, demonstrating the effectiveness and validity of the representation
2. showing the effect of meta-agents on the computational designers in the section ‘Meta-agents for multiagent design’, showing how the multidisciplinary design process is affected by designers’ preferences for exploration over time, and
3. showing how synchronization and independence of computational designers affects multiagent design in the section ‘Collaboration and decomposition in multiagent design’ to study collaboration in multidisciplinary design.
The results are discussed in their respective sections and summarized in the section ‘Summary’.
Viability of the multiagent design method
The following tests compare the effectiveness of the decentralized multiagent optimization method with existing centralized optimization methods to show the effectiveness of the method for complex systems design in order to demonstrate the validity of the representation. This is important because the validity of the problem representation forms the basis for the validity of the results presented in the sections ‘Meta-agents for multiagent design’ and ‘Collaboration and decomposition in multiagent design’, and is being used to make conclusions about the design process. Therefore, it is important to show that this method is a viable optimization method, and not simply an optimizing process which may, due to some flaw in process or implementation, reach an artificial minimum. To test this, this paper compares the method presented here with a common stochastic optimization method (a genetic algorithm), and a stochastic hill-climbing algorithm which we expect to perform poorly by reaching a local minimum – essentially showing the behavior expected from a flawed stochastic optimizing process.
The comparison methods are a centralized genetic algorithm and a stochastic hill-climbing algorithm. This centralized genetic algorithm was set up using default parameters for MATLAB's ga function, with 200 generations of population 100 to show how a global optimization method searches the space. The stochastic hill-climbing algorithm was set up using MATLAB's simulannealbnd function by choosing a low temperature (T = 5) to simulate stochastic hill-climbing to simulate how a flawed stochastic optimization process would search the space, as it is known that stochastic hill-climbing will converge to a local minimum. Custom annealing functions for the mixed continuous-integer problem to show how an optimizer that gets stuck in local optima searches the space. These comparisons give a picture of whether the algorithm developed in this paper is capable of global optimization (causing performance comparable with the centralized genetic algorithm) or is prone to get stuck in local minima (causing performance comparable to stochastic hill-climbing).
Figure 5 shows the general trend of the distributed multiagent optimization method using the global reward structure compared with centralized optimization methods like the genetic algorithm and stochastic hillclimbing over 20,000 objective function evaluations by showing the median value of the optimization and distribution of results over 10 runs. Throughout the process, the multiagent method outperforms the centralized genetic algorithm, reaching better objective values in less computational time. In addition to showing the general optimization effectiveness of the method, this result also shows the ability of the method to not get caught in early local minima, as is the case with stochastic hill-climbing on this domain. This shows that the method indeed optimizes without obvious process flaws holding it back. Additionally, the final results distribution shows that the overall variability in results of the method is similar or better than the comparison algorithms, showing that the method finds the minimum reliably. While this result shows the general effectiveness of the method, it should be noted that it is not a comprehensive comparison – just a check to confirm the validity of the method. While it shows the multiagent method to perform well on this problem, future work is needed to show how it performs on a variety of problems to judge its effectiveness in practice.
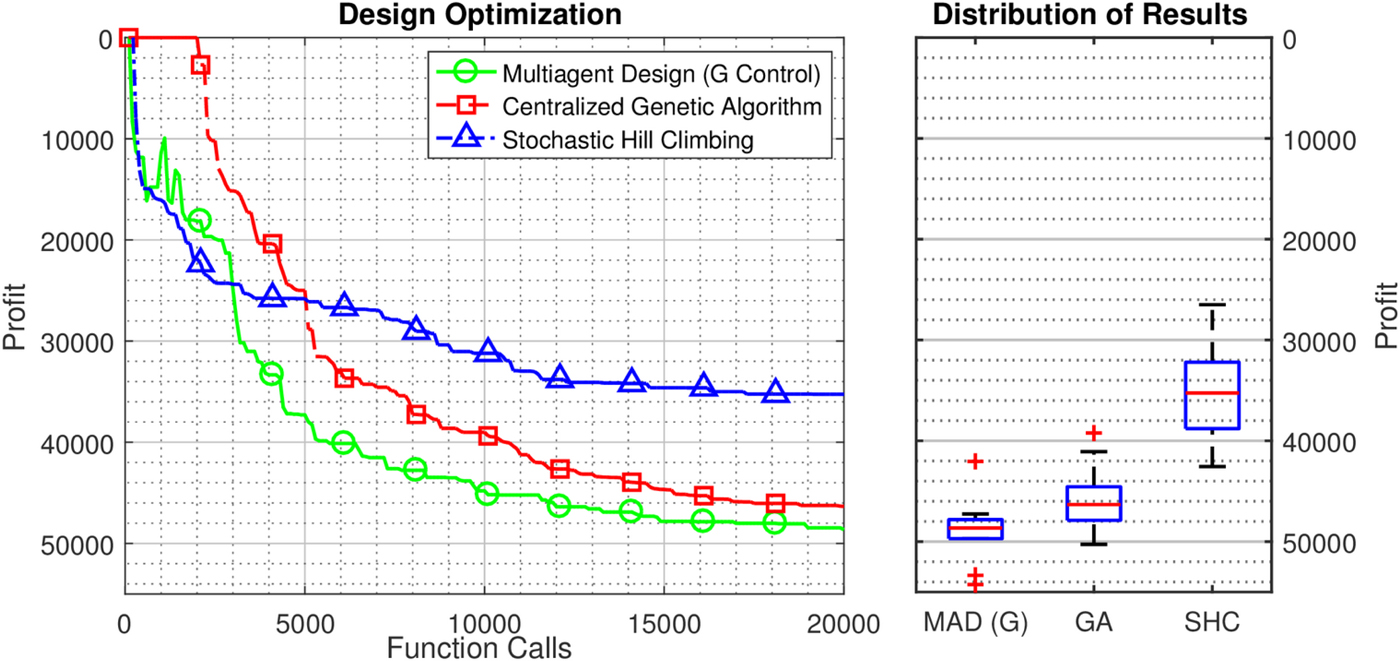
Fig. 5. Performance of multiagent design compared with a centralized genetic and stochastic hill-climbing algorithm. Multiagent design outperforms both, demonstrating the validity of the optimization method introduced in the section ‘Multiagent learning-based design optimization method’.
Meta-agents for multiagent design
The following tests show the effect of different methods of controlling the multidisciplinary design process by comparing the reinforcement-learning meta-agents introduced in the section ‘Meta-agents for multiagent design’ with annealing and a random table selection. Annealing was used in previous work by the authors as a heuristic to control the exploration/exploitation parameter τ of the agents (Hulse et al., Reference Hulse, Gigous, Tumer, Hoyle and Tumer2017), so this result demonstrates further development of this algorithm to model exploratory design behavior. Additionally, a random selection of temperatures from the same tables the agents choose from is presented to give a control for how much reinforcement learning meta-agents really improve the process. Two reward structures – the “global reward” based on the improvement of all of the agents' value functions and the “local reward” based on the improvement of the individual agent's value function – are additionally compared to show how rewards influence the performance of the meta-agent.
The results are shown in Figure 6. As can be seen, agent-based table selection (denoted by “Random Control,” “G-Control,” and “L-Control”) vastly outperforms decaying temperatures over the entire optimization process. Additionally, a few different trends are visible for the controllers. First, controlling using the global reward, while slow to start, outperforms a random control strategy at about 75,000 function calls, settling in a lower minima than a random strategy by the end of the optimization. The random control strategy, on the other hand, seems to find good solutions quickly (in the first 75,000 iterations or so) compared with the other strategies but loses this advantage later in the process. Finally, the local reward actually decreases the performance of the algorithm compared to random at each step of the process, although it does outperform the global reward in the first 5000 iterations.

Fig. 6. Impact of meta-agent on multiagent design. Learning improves performance over random table selection using the global reward (G) and decreases performance using the local reward (L). All strategies outperform decaying temperatures over time.
These results provide interesting insights, both for the development of this optimization method and for distributed design in general. First, it shows how reinforcement learning can be used to increase the performance of this optimization algorithm, and how, in this case, the reward structure can improve or hinder that control. Reinforcement learning, which is used to maximize rewards in a dynamic and probabilistic environment, has been shown here to increase the performance of the optimization algorithm when used with a reward system that promotes exploration based on the increase in knowledge gained by that exploration. Second, it shows how annealing – converging on a single solution over time, reducing the impact of possible changes that may be made – may not be a preferred behavior for designers that are distributed across disciplinary boundaries. Previously, annealing has been used as a model for design processes, as designers will often explore the design space for changes before slowly converging around a design, reducing the impact of proposed design changes over time (Cagan and Kotovsky, Reference Cagan and Kotovsky1997; McComb et al., Reference McComb, Cagan and Kotovsky2015a; Reference McComb, Cagan and Kotovsky2015b). While both these approaches had some level of built-in adaptiveness that allowed them to explore newly-found parts of the design space through re-annealing, this result shows how annealing without any adaptiveness may lead to sub-optimal outcomes in a multidisciplinary context when trying to find an optimal set of interacting components.
Instead, this result shows that it is far better for the purposes of design exploration to continue to explore at all levels at all times of the process (random selection) and even better to explore changes which increase the collective knowledge about the design space (learning-based control with the G reward structure). It should be noted for this discussion that the designers not decaying their preference for exploration does not mean that they should consider all designs equal throughout the design process – design merit knowledge (encoded in the sub-agent) is still always used to generate a design change. Instead, this means knowledge should be sought out or leveraged at varying degrees throughout the process that should not be based on the progression through the design process. Based on this result, design exploration and exploitation is beneficial if the designer exploring variables (or keeping their variables constant so that others may explore) reveals unknown parts of the design space that are better than expected, regardless of the progression through the design process. While, in practice, it may be necessary to solidify parts of the design to perform more detailed design work, this result shows that slowly and permanently solidifying the entire design while exploring the design space can prevent the designers from finding the best-performing design. Instead, this result suggests that designers should instead be incentivized by the increase in design knowledge that their exploration causes. This is an important insight for the early and embodiment design stages when the goal is not a fully analyzed detailed design, but an optimal set of interacting component parameters to be used as a basis for further design.
Collaboration and decomposition in multiagent design
The following results compare the effects of designers designing independently or collaboratively. This is represented by allowing the computational designers to submit changes synchronously, with only individual components designed synchronously, or with all variables chosen asynchronously. This is how a design team that collaborates or treats components as independent would behave – if designers communicate and interact, they investigate joint changes between subsystems. On the other hand, if designers remain autonomous, they will only see how their own subsystem changes overall performance, and will make changes individually. While independent component changes most realistically represent this problem, independent variable changes are shown to further illustrate the trend.
Figure 7 shows the influence of these three behaviors – collaboration, component asynchrony, and variable asynchrony – on the best objective function found by the algorithm over ten runs. As can be seen, there is a significant difference in performance between both the trends of these design processes and the final results. While collaboration continues to improve performance throughout the iterations in the test, both asynchronous design strategies seem to reach process minima, or “floors” mid-way through, after which they are unable to efficiently improve the design. Additionally, the asynchronous variable design strategy seems to be more efficient in the earlier stages, but more quickly stops improving, while the asynchronous component design strategy is slower in the early stages but continues improving, if slowly.
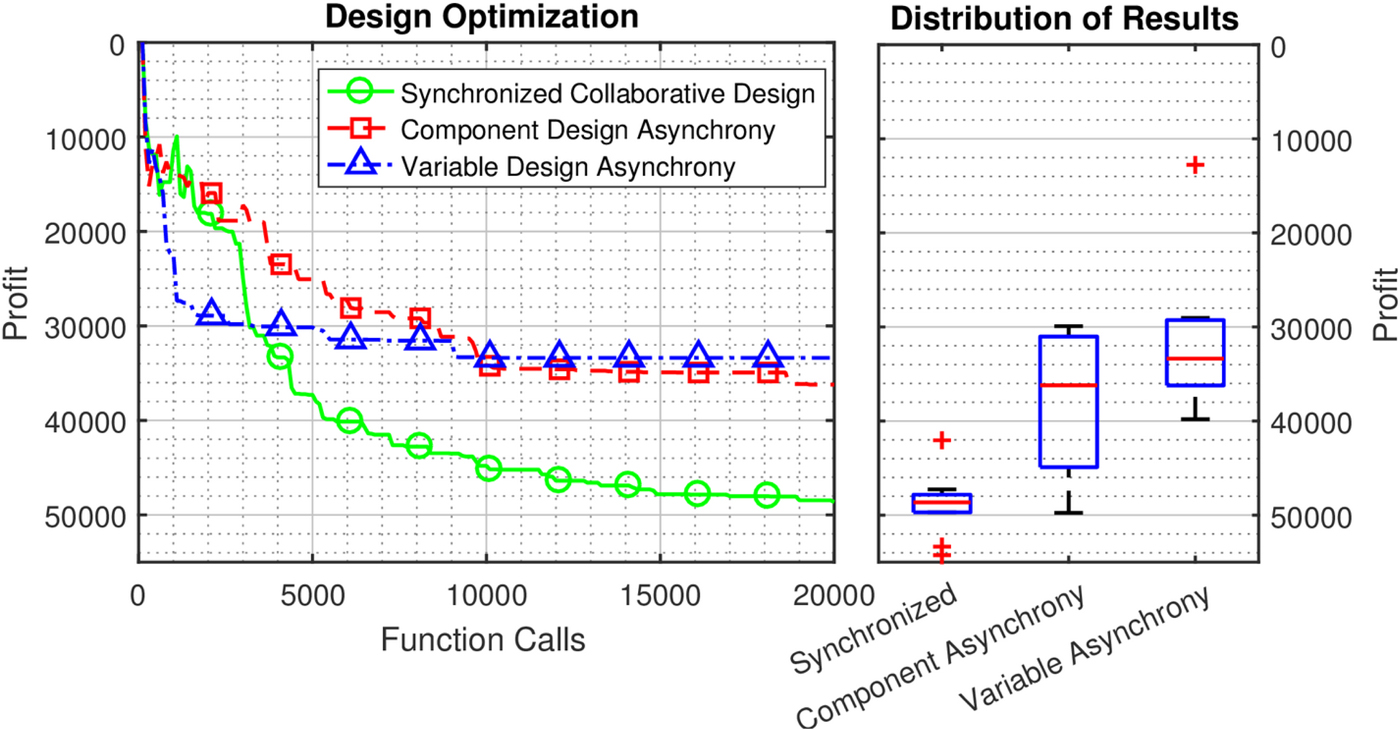
Fig. 7. Effect of synchronization on agents’ ability to design. Agents are better able to optimize when they collaborate by designing synchronously than when they are decomposed into groups (by component or by variable) which design asynchronously.

Algorithm 1. Control logic for sub-agent merit update and subsequent meta-agent rewards.
Intuitively, it is easy to understand why asynchrony causes the algorithm to prematurely stop improving the design. One of the major defining features of complex engineered systems is the interconnections between components – it is often said that “the inputs of one subsystem are the outputs of another subsystem” (Kroo et al., Reference Kroo, Altus, Braun, Gage and Sobiesky1994). As a result, the overall performance of the system is related not just to an individual component's contribution, but how different components work together. Therefore, combined changes between components must occur for a design process to be effective. This can be understood by reconsidering the simple game-theoretic design problem in Figure 1. If the designers are currently at design A–A (a sub-optimal Nash equilibrium), they can not proceed to design B–B (the optimal Nash equilibrium) without both agents collaborating, as the non-collaborative paths from A–A to B–B require the agents accepting incompatible designs. In the multidisciplinary context, this must be done through communication and collaboration between designers, which enables designers to design perform changes which happen in multiple subsystems at the same time.
In addition to making intuitive sense, these results confirm findings of design research about integrated concurrent engineering and suggest a mechanic by which increasing collaboration can produce higher-value solutions. The conclusion most often reached by research studying integrated concurrent engineering is that it decreases the total time in producing a design compared with a more siloed or independent design process (Smith, Reference Smith1998; Mark, Reference Mark2002). The typical explanation for this is that radical co-location enables engineers to complete a design more quickly because of fewer communication delays – engineers design quicker because they can speak face-to-face with the designers of connected subsystems, rather than waiting for an email to return (Chachere et al., Reference Chachere, Kunz and Levitt2009). However, this result shows that decreasing communication barriers between designers can not only increase solution time but also solution quality because of the coupled nature of complex engineered systems. While all design processes were able to reach designs which satisfied requirements by meeting constraints, the collaborative design process did not get stuck in process minimums caused by Nash equilibria like the independent processes did. This is because the designers in the multiagent system could make combined changes which allowed the optimization process to navigate inter-component constraints. This suggests that the relative ease of making combined changes in an integrated collaborative engineering process should also allow design teams to produce higher-quality designs in addition to achieving a faster design process.
Summary
The results presented in the previous sections are summarized in Table 4, in terms of the median and standard deviation of the optimums found, the constraint violation at the final iteration (using ![]() $\sum\nolimits_{j = 1}^n {\hbox{c}_j^2} $), and important model parameters, including mass, component cost, energy stored, and mission time. Note that these model parameters are not considered objectives in themselves, but are instead taken into account using the mission model, which calculates the objective based on the value of a theoretical mission (labeled profit). As can be seen, the parameters most correlated with the objective are mission time and stored energy, while others such as component cost and mass do not correlate well with the objective, likely due to the smaller influence of component cost and mass compared with mission revenue and energy storage in the model. In summary, all methods were able to produce feasible designs, but the best-performing method was using the multiagent method with controlled by reinforcement learners rewarded by the global exploratory reward.
$\sum\nolimits_{j = 1}^n {\hbox{c}_j^2} $), and important model parameters, including mass, component cost, energy stored, and mission time. Note that these model parameters are not considered objectives in themselves, but are instead taken into account using the mission model, which calculates the objective based on the value of a theoretical mission (labeled profit). As can be seen, the parameters most correlated with the objective are mission time and stored energy, while others such as component cost and mass do not correlate well with the objective, likely due to the smaller influence of component cost and mass compared with mission revenue and energy storage in the model. In summary, all methods were able to produce feasible designs, but the best-performing method was using the multiagent method with controlled by reinforcement learners rewarded by the global exploratory reward.
Table 4. Summary of results
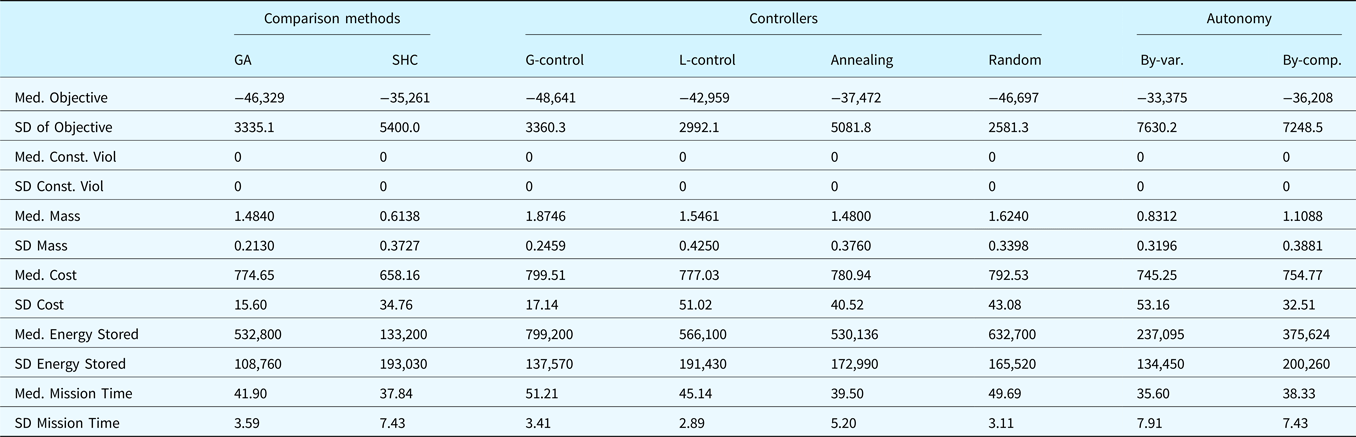
Shown are the median and standard deviation of the optimum objective, constraint violation, mass, cost, energy stored, and mission time for each of the methods tested in the paper: the genetic algorithm and stochastic hill-climbing comparison methods, the multiagent method controlled using the global reward, local reward, a temperature decay and random temperature selection, and the multiagent method using by-variable autonomy and by-component autonomy
Conclusions
This paper introduces a new multiagent optimization method which may be used to model the multidisciplinary engineering process by distributing authority over variables in the design problem to computational designers represented as sets of learning agents. This optimization method was shown to perform similarly to a centralized genetic algorithm applied to the same domain when using reinforcement learning and an exploratory reward to control the agents. Additionally, this learning-based control (and even random control) was shown to outperform annealing, calling into question the idea that engineers should converge on a design in the early design exploration stages. It instead suggests that designers in a collaborative multidisciplinary setting should explore potentially high or low-impact changes throughout the design exploration process based on the increase in design knowledge. Finally, a collaborative process in which designers propose design changes collaboratively at the same time was shown to perform much better than a process in which designers propose changes independently at different times. This result suggests a mechanism by which increased cooperation can increase design quality: the ability to explore joint design changes which would otherwise be unavailable if the system was designed independently.
Future work
Future work will focus on improving the method and demonstrating the insights gained using the method in real-world scenarios. A full, comprehensive comparison between this method and others could be shown to characterize the performance on various model domains. While the rewards used here were shown to perform well, future work could show if other rewards would increase performance further. Additionally, a study of the effectiveness of the difference reward could be done, showing how to balance the computational costs of the reward with the benefits. Finally, while the conclusions that lowering the impact of design changes over time (annealing) decreases design performance and increasing collaboration can lead to better solution quality provide interesting insights into the complex engineered system design process, real-world tests should be done to validate that these conclusions hold in practice.
Daniel Hulse is a Graduate Research Assistant at Oregon State University's Design Engineering Lab. He is interested in using novel modeling and optimization techniques to inform and aid the design process. Specifically, he is interested in developing formal design frameworks and instructive models to overcome designers’ inherent bounded rationality when designing complex systems, and in using optimization algorithms to explore large spaces of solutions to a design problem.
Dr Kagan Tumer is Professor and the Director of the Collaborative Robotics and Intelligent Systems (CoRIS) Institute at Oregon State University. His research focuses on multiagent coordination, machine learning and autonomous systems. He has ~200 peer-reviewed publications and holds one US patent. He was program chair for the 2011 Autonomous Agents and Multi-Agent Systems (AAMAS) conference. His work has received multiple awards (including the best paper awards at the Autonomous Agents and Multiagent Systems Conference in 2007 and the best application paper award at the Genetic and Evolutionary Computation Conference (GECCO) in 2012.
Dr Christopher Hoyle is currently Associate Professor in the area of Design in the Mechanical Engineering Department at Oregon State University. His current research interests are focused upon decision making in engineering design, with emphasis on the early design phase. His areas of expertise are uncertainty propagation methodologies, Bayesian statistics and modeling, stochastic consumer choice modeling, optimization and design automation. He is a coauthor of the book Decision-Based Design: Integrating Consumer Preferences into Engineering Design. He received his PhD from Northwestern University in Mechanical Engineering in 2009 and his Master's degree in Mechanical Engineering from Purdue University in 1994.
Dr Irem Y. Tumer is a Professor in Mechanical Engineering at Oregon State University, and Associate Dean for Research for the College of Engineering. Her research focuses on the challenges of designing highly complex and integrated engineering systems with reduced risk of failures, and developing formal methodologies and approaches for complex system design, modeling, and analysis, funded through NSF, AFOSR, DARPA, and NASA. Prior to coming to OSU, Dr Tumer worked in the Intelligent Systems Division at NASA Ames Research Center, where she worked from 1998 through 2006 as Research Scientist, Group Lead, Program Manager. She is an ASME Fellow.