1. INTRODUCTION
Scheduling becomes necessary whenever a common set of resources in the manufacturing system must be shared in order to make several different products during the same period of time. The aim of manufacturing scheduling is to efficiently allocate machines and other resources to jobs, or operations within jobs, and then carry out the subsequent time phasing of these jobs on individual machines (Shaw et al., Reference Shaw, Park and Raman1992). Scheduling problems include three components: a machine environment, specific job characteristics, and one or more optimality criteria (Brucker, Reference Brucker2001).
The machine environment represents the type of the manufacturing system that will carry out the execution of the schedule. The manufacturing system can be any of the following: a job shop system, a flexible manufacturing system (FMS), a cellular manufacturing system, a transfer line, and so forth. Job characteristics represent different factors, such as the number of operations, the precedence relations among operations, and the possibility of preemption. Optimality criteria are the objectives to accomplish. Common objectives include minimizing makespan, mean flow time, mean lateness, the number of tardy jobs, and mean tardiness. All three components mentioned above specify the variety and complexity of each scheduling problem (Wang & Usher, Reference Wang and Usher2005). A scheduling problem may comprise two subproblems: job routing and job sequencing problems. The first subproblem involves assigning the job operations to the machines. These problems appear when routing flexibility is allowed. In the second case, once the route of a job is specified, the sequence of the jobs awaiting their next operation in the machine queue is calculated (Wang & Usher, Reference Wang and Usher2005).
Most manufacturing systems operate in dynamic environments where usually unavoidable unpredictable real-time events (e.g. machine failures, arrival of urgent jobs, due date changes, etc.) may cause a change in the schedule, and a previously feasible schedule may lose its feasibility when it is released on the manufacturing system. The problem of scheduling in the presence of real-time events, known as dynamic scheduling, is of great importance to the successful implementation of real-world scheduling systems (Ouelhadj & Petrovic, Reference Ouelhadj and Petrovic2009). Three categories of dynamic scheduling have been defined: completely reactive, predictive–reactive, and robust proactive. Predictive–reactive scheduling is the most common dynamic scheduling approach used in manufacturing systems and is based on revising the schedules in response to real-time events (Ouelhadj & Petrovic, Reference Ouelhadj and Petrovic2009).
Rescheduling needs to study two issues: how and when to react to real-time events. Regarding the first matter, the literature provides two main rescheduling strategies (Sabuncuoglu & Bayiz, Reference Sabuncuoglu and Bayiz2000; Cowling & Johansson Reference Cowling and Johansson2002; Vieira et al., Reference Vieira, Herrmann and Lin2003): schedule repair and complete rescheduling. Regarding the second issue, three policies have been proposed in the literature (Sabuncuoglu & Bayiz, Reference Sabuncuoglu and Bayiz2000; Vieira et al., Reference Vieira, Herrmann and Lin2003): periodic, event-driven, and hybrid rescheduling. In the periodic policy, the dynamic scheduling problem is broken down into a series of static problems that can be solved by using classical scheduling algorithms (Ouelhadj & Petrovic, Reference Ouelhadj and Petrovic2009).
The different approaches used to solve the problem of scheduling can be divided into the following categories: analytical, heuristic, simulation, and artificial intelligence approaches. The analytical procedure interprets a scheduling problem as an optimization model with certain constraints, in terms of an objective function and explicit constraints. An appropriate algorithm is then used to solve the model (see, e.g., Stecke, Reference Stecke1983; Kimemia & Gershwin, Reference Kimemia and Gershwin1985; Shanker & Tzen, Reference Shanker and Tzen1985; Lashkari et al., Reference Lashkari, Dutta and Padhye1987; Han et al., Reference Han, Na and Hogg1989; Wilson, Reference Wilson1989; Bertel & Billaut, Reference Bertel and Billaut2004; Pan & Chen, Reference Pan and Chen2005). In general, these problems are of an NP-complete type (Garey & Johnson, Reference Garey and Johnson1979).
The classical job shop scheduling problem is one of the most well-known scheduling problems. The problem is to decide the start time of each job on each one of the machines needed, in order to optimize a desired performance criterion. This problem is constrained by a precedence constraint that means no operations on a job can be started until all previous operations are completed and no two operations from two different jobs may be performed simultaneously on the same machine (El-Bouri & Shah, Reference El-Bouri and Shah2006).
Metaheuristics [e.g., simulated annealing (SA), tabu search, genetic algorithms (GAs)] have been widely applied to solve static deterministic scheduling problems in several domains. However, hardly any research work has addressed the use of metaheuristics in dynamic scheduling (Ouelhadj & Petrovic, Reference Ouelhadj and Petrovic2009). Metaheuristics have an advantage over dispatching rules in terms of solution quality and robustness; nevertheless, these are usually more difficult to implement and tune, and are computationally too complex to be applied in a real-time system (Shahzad & Mebarki, Reference Shahzad and Mebarki2012).
Many researchers (see, e.g., Panwalkar & Iskander, Reference Panwalkar and Iskander1977; Stecke & Solberg, Reference Stecke and Solberg1981; Blackstone et al., Reference Blackstone, Phillips and Hogg1982; Baker, Reference Baker1984; Denzler & Boe, Reference Denzler and Boe1987; Vepsalainen & Morton, Reference Vepsalainen and Morton1987; Montazeri & Van Wassenhove, Reference Montazeri and Van Wassenhove1990; Tang et al., Reference Tang, Yih and Liu1993) have assessed the performance of the dispatching rules on manufacturing systems by means of simulation. The conclusion to be drawn from these studies is that their performance depends on many factors, such as the criteria selected, the system's configuration, and the workload (Cho & Wysk, Reference Cho and Wysk1993).
While taking into consideration the variable performance of dispatching rules, it would be interesting to modify these rules dynamically and at the right moment for the system's conditions. The assumption that this approach will be better than the conventional system of using a constant dispatching rule is an a priori assumption for two reasons. First, because it can identify the best rule for a given manufacturing scenario. Given such a selection capacity, the system should perform at least as well as the best dispatching rules being considered. Second, this approach can adapt its choices dynamically to changing scenarios. This adaptability should result in job scheduling with a higher quality than even the best dispatching rules (Shaw et al., Reference Shaw, Park and Raman1992).
Basically, two approaches to the dynamic modification of dispatching rules can be found in the literature. In the first approach the rule is selected at the appropriate moment by simulating a set of preestablished dispatching rules and choosing the one that provides the best performance (see, e.g., Wu & Wysk, Reference Wu and Wysk1989; Ishii & Talavage, Reference Ishii and Talavage1991; Kim & Kim, Reference Kim and Kim1994; Jeong & Kim, Reference Jeong and Kim1998; Kutanoglu & Sabuncuoglu, Reference Kutanoglu and Sabuncuoglu2001). The main drawback to these simulation-based systems is the time required to examine the performance of the set of candidate rules, which can make real-time scheduling difficult. In addition, no knowledge about the system is acquired.
To overcome these limitations, in the second approach, based on the artificial intelligence field, a set of earlier system simulations (training examples) is used to determine which rule is the best for each possible system state. These training cases are used to train a machine learning module to acquire knowledge about the manufacturing system. Such knowledge is then used to make intelligent decisions in real time. These scheduling systems are usually said to be knowledge based.
This article reviews different papers published over the last ten years that use the second approach and thereby update the work presented in Priore, De la Fuente, Gómez, et al. (Reference Priore, De la Fuente, Gómez and Puente2001). The rest of this paper is organized as follows. The knowledge-based scheduling system is defined in detail in Section 2. Section 3 is a review of the work done in this type of scheduling system and a description of its main characteristics. Section 4 provides a discussion of a series of generalized shortcomings regarding knowledge-based systems that need to be dealt with in future research. Section 5 contains the conclusion.
2. KNOWLEDGE-BASED SYSTEMS
A real-time scheduling system that modifies dispatching rules dynamically should fulfill two contradictory characteristics in order for it to work adequately (Nakasuka & Yoshida, Reference Nakasuka and Yoshida1992):
1. The rule selection must contemplate different information about the manufacturing system in real time.
2. The rule selection must be completed in such a short amount of time that real operations are not delayed.
One way of achieving these characteristics is to use knowledge about the relationship between the manufacturing system's state and the rule that is to be applied at that moment. It is therefore useful to use “scheduling knowledge” of the manufacturing system to save time and to obtain a rapid response in a dynamically changing environment. However, one of the most difficult problems to solve in a knowledge-based system is precisely how this knowledge is to be acquired.
In order to acquire knowledge, machine learning techniques, such as inductive learning or neural networks (NNs), are used. The latter reduce the effort involved in determining the knowledge that is needed for making scheduling decisions. However, the training examples and the learning algorithm must be right for this knowledge to be useful. Moreover, in order to get the training examples, the attributes that are selected are crucial for the performance of the scheduling system that is generated (see, e.g., Chen & Yih, Reference Chen and Yih1996; Su & Shiue, Reference Su and Shiue2003).
There are at least four reasons why a knowledge-based approach might perform worse than the best rules when used constantly (Priore, De la Fuente, Gómez, et al., Reference Priore, De la Fuente, Gómez and Puente2001):
1. The training set is a subset of all the possible cases. However, situations in which the scheduling system does not work properly can always be observed and added as training examples.
2. The system's performance depends on the number and range of control attributes taken into account when designing the training examples.
3. A rule may perform well in a simulation over a long period of time for a given set of attributes, but it may perform poorly when applied dynamically.
4. The system can be prone to inadequate generalizations in extremely imprecise situations.
An overview of a scheduling system that uses machine learning is shown in Figure 1. A simulation model is used by the example generator in order to create different manufacturing system states and to choose the best dispatching rule for each particular state. The machine learning algorithm acquires the knowledge necessary to make future scheduling decisions from the training examples. The real-time control system using the “scheduling knowledge,” the manufacturing system's state and performance, determines the best dispatching rule for job scheduling. Depending on the manufacturing system's performance, the knowledge may need to be refined by generating further training examples.

Fig. 1. The general overview of a learning-based scheduling system.
3. REVIEW OF KNOWLEDGE-BASED APPROACHES
Next, several knowledge-based approaches that dynamically modify the dispatching rule being used in a specific instance are reviewed. Depending on the type of machine learning algorithm used, these approaches can be divided into the following categories: inductive learning, NNs, case-based reasoning (CBR), support vector machines (SVMs), reinforcement learning, mixed approaches, and other approaches.
3.1. Inductive learning based approaches
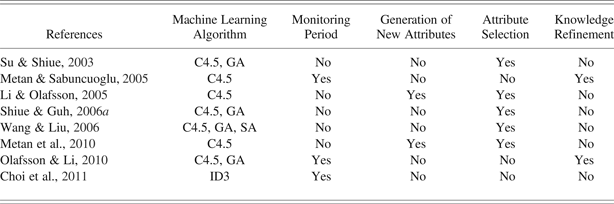
Su and Shiue (Reference Su and Shiue2003) propose a technique that integrates GAs with inductive learning in order to create an intelligent scheduling system. A GA is used to search for all possible subsets of a large set of system attributes. For a given attribute subset, the inductive learning algorithm is applied, and it generates a decision tree. The decision tree is used to classify unseen data and measure the fitness of the given attribute set. This process continues until an attribute subset reaches a satisfactory classification performance. The case study involves a modification of the model used by Montazeri and Van Wassenhove (Reference Montazeri and Van Wassenhove1990). During the experimental study, the proposed technique is compared with the use of a single inductive learning module and with dispatching rules that are constantly used. In this study, 2000 training examples are used, and the latter are based on three performance criteria: throughput, mean flow time, and number of the tardy parts. The algorithm of inductive learning used is C4.5 (Quinlan, Reference Quinlan1993). The results obtained show that the proposed technique provides higher performance for the mean flow time and the number of tardy parts criteria. The percentages of the progress made fluctuate between 1.83% and 22.18%. However, for the throughput criterion, the results achieved with the proposed technique are very similar to those obtained with the other two techniques. In addition, the authors indicate that the use of an optimum subset of system attributes increases the classification performance. The improvement percentages vary between 32.42% and 22.81%, depending on the performance criteria of the manufacturing system that are used.
Metan and Sabuncuoglu (Reference Metan, Sabuncuoglu, Kuhl, Steiger, Armstrong and Joines2005) developed a system that uses inductive learning techniques, process control charts, and simulation. In the proposed system, a decision tree is created by using the characteristics of the manufacturing system, and the dispatching rules are selected from that tree for each scheduling period. The inductive learning algorithm used is C4.5. Control charts are used to monitor the performance of the decision tree. If these charts show that the performance of the tree begins to decline, a new one is built from information that has recently been obtained from the manufacturing system by means of simulation. The proposed approach is implemented in a job shop system (Baker, Reference Baker1984), and its objective is to minimize the average tardiness under various conditions of system usage, monitoring, and scheduling period lengths and different sets of dispatching rules, among other parameters. The results indicate that it is important to select appropriate values for the period of scheduling, monitoring, and the parameter β (the parameter that decides whether to update or continue the current dispatching rule). It also makes sure that the proposed system works better than the classic multipass and single-pass systems. However, for large values in the monitoring interval, the performance of the proposed mechanism decreases and becomes similar to the multipass method. In contrtast, the addition of competitive dispatching rules improves the performance of the proposed system and the multipass method.
Li and Olafsson (Reference Li and Olafsson2005) introduce a new methodology for generating new scheduling rules directly from the production information. The authors say that an advantage of the proposed system is that the implicit knowledge of expert schedulers is discovered and can be applied to generate future schedules. In addition to the latter, existing scheduling practices are generalized into explicit scheduling rules. Structural knowledge leading to new rules, which would improve performance, may be gained. The proposed method has two phases: (1) data preparation including aggregation, attribute construction, and attribute selection and (2) model induction and interpretation. The inductive learning algorithm used is C4.5. In the experimental study, different single machine scheduling problems are tested. The results reached with the proposed technique are compared with those obtained when the jobs are ordered according to four dispatching rules [earliest due date (EDD), weighted shortest processing time (WSPT), minimum slack (MS), earliest release date (ERD)]. Three different problem sizes are used, with the goal of minimizing the makespan. The results indicate that in 9 of the 12 cases in the study, the difference in the performance of the proposed methodology and the dispatching rules is less than 2%. The ERD rule shows results that are the most similar, while the greatest difference (with a maximum of 8.3%) is seen with the WSPT rule. The authors say that because the purpose of the decision trees is to learn the scheduling concept, not to improve upon it, when the trees are used as dispatching rules, they do not expect the performance to be better than the original. However, if the trees do discover the relevant concepts, then the performance should be similar to the original rules.
Shiue and Guh (Reference Shiue and Guh2006a) improve upon the work presented in Su and Shiue (Reference Su and Shiue2003), proposing a technique that uses inductive learning and GAs to simultaneously determine an optimal subgroup of system attributes and the parameters of the C4.5 inductive learning algorithm. In the experimental study, the proposed system is compared with the others that only use inductive learning, backpropagation NNs (BNNs), and continuously applied rules. The results attained demonstrate that the proposed technique presents better performance for the mean flow time and the number of tardy parts criteria. The enhancement percentages fluctuate between 3.53% and 27.50%. However, for the throughput criterion, the results obtained with the proposed technique are very similar to those obtained with the three other techniques. In addition, there are no significant differences between the classic learning systems and the best dispatching rule when used constantly. Finally, with the proposed methodology, a better classification performance is obtained when compared with the NNs or with inductive learning in those that do not use the mechanism of attribute selection.
Wang and Liu (Reference Wang and Liu2006) modify a standard GA incorporating SA that acts as an adaptive mutation operator. This optimization method, called GASA, can achieve more efficient optimization results and relax the dependence on the empirical parameters to a certain extent. This hybrid method was used to obtain the optimal subset of manufacturing system attributes and determine the optimal parameters of the C4.5 algorithm under different performance criteria. The case study includes a variation of the model implemented by Montazeri and Van WassenHove (Reference Montazeri and Van Wassenhove1990). The proposed mechanism is compared with other algorithms involving the acquisition of knowledge, based on machine learning, such as NNs, inductive learning, and the system proposed by Shiue and Guh (Reference Shiue and Guh2006a) that uses inductive learning and GAs. The results show that the knowledge bases, obtained using the proposed algorithm, have better generalization accuracy than those obtained with the other mechanisms. For example, for the criterion of mean flow time, the largest generalization ability is obtained with GASA and is 44.70%, 41.74%, and 11.68% higher than the one provided by inductive learning, NNs, or by the combination of inductive learning and GAs, respectively.
Metan et al. (Reference Metan, Sabuncuoglu and Pierreval2010) continue the work presented in Metan and Sabuncuoglu (Reference Metan, Sabuncuoglu, Kuhl, Steiger, Armstrong and Joines2005) and also illustrate knowledge extraction by presenting a sample decision tree from their experiments. The authors say that they can extract the information hidden and dissolved in the data concerning the conditions and circumstances that make a dispatching rule more efficient and desirable over other rules. The authors also indicate that this expertise can be used for designing new and more efficient dispatching rules, categorizing existing rules, and for providing more insights to practitioners in the industry.
Olafsson and Li (Reference Olafsson and Li2010) propose an extension of the work presented in Li and Olafsson (Reference Li and Olafsson2005). In this new approach, a GA carries out the selection of training examples in order to identify which part of the information corresponds with the best scheduling practices. Finally, by using an inductive learning algorithm (C4.5), data that are chosen in the previous phase are used to generate a decision tree for learning new dispatching rules that were previously unknown. In the experimental study, a system with only one machine and 10 jobs is used. The results obtained are compared with those obtained with a scheduling system that does not use a GA to choose the most relevant data for learning. The results acquired demonstrate that this use of the selection of data provides better decision trees, which are smaller, easier to explain, and show better performance. The weighted maximum lateness is reduced to between 38% and 55%, in comparison with the trees that do not use data selection.
Choi et al. (Reference Choi, Kim and Lee2011) present a real-time scheduling mechanism that uses inductive learning for reentrant hybrid flow shops. The proposed mechanism is compared with a system based on simulation for the throughput, mean flow time, mean tardiness, and number of tardy jobs criteria. The learning algorithm used is the ID3 (Quinlan, Reference Quinlan1986). In the experimental study a real thin film transistor-liquid crystal display manufacturing system is used. From the results that are obtained in the experimental study, the differences in performance between the two systems are not significantly large.
3.2. NN-based approaches
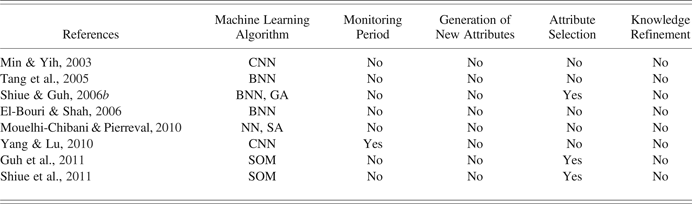
Min and Yih (Reference Min and Yih2003) propose a scheduler for the selection of dispatching rules in order to obtain the desired performance measures given by a user for each production interval. In the proposed methodology, competitive NNs (CNNs) are used. Initially, a simulation experiment is conducted to collect the data containing the relationship between the change of the decision rule set and the current system status and performance measures. The scheduling system chooses rules for the machines and the automated material handling systems. Next, using the data obtained in the simulation, a CNN is used to obtain the scheduling knowledge. The scheduler will then choose the appropriate rules when the correct performance measures are supplied along with the status of the manufacturing system. The semiconductor fab model in this study imitates a fab of LG Semiconductor Company in Korea (Wein, Reference Wein1988). During the study, 1500 pieces of unclassified data are collected, making up the training examples. These are used in three different experiments with three different load levels in the critical machine. Three performance measures are used: mean flow time, mean slack time, and mean remaining processing time. The proposed methodology is checked to make sure it is suitable for such complex manufacturing systems owing to the reentrant product flow.
Tang et al. (Reference Tang, Liu and Liu2005) present a dynamic scheduling model in a hybrid flow shop system based on the use of NNs. The authors suggest the use of a subneural network for each of the performance measures that are to be optimized. These subnetworks can be trained both simultaneously and separately, thereby obtaining a reduction in the training time. Owing to the slow convergence of the training algorithm of a BNN, a delta–bar–delta algorithm is also used in order to further speed up the convergence of the training process. This algorithm adjusts the learning rate of the training process dynamically based on the variation of training error and optimizes the training process. In the experimental study, the proposed technique is used in a flow shop system, and 96 training examples, obtained from the simulation, are used to train each of the three subneural networks. The results accomplished are compared with those obtained by constantly using the dispatching rules. Different usage levels and due dates are taken into account. The objectives are to minimize the average flow time, the average tardy time, and the percentage of tardy jobs. The results show that, although the proposed method is not always the best, it is the only method that can give consistently good performance under all three performance criteria.
Shiue and Guh (Reference Shiue and Guh2006b) propose a scheduling system based on BNNs that use GAs in order to select the optimal subgroup of system attributes and simultaneously determine the topology and learning parameters of the NN. The case study concerns an adaptation of the model put in practice by Montazeri and Van Wassenhove (Reference Montazeri and Van Wassenhove1990). The results accomplished by the proposed technique are compared with those with the classic application of the NNs, inductive learning, and the dispatching rules when constantly used. The results obtained show that the proposed technique presents higher performance for the mean flow time and the number of tardy parts criteria. The percentages of the betterment fluctuate between approximately 6.21% and 26.03%. However, for the throughput criterion, the results attained with the proposed technique are very similar to those obtained with the other three techniques. In addition, there are no significant differences between the classic learning systems and the best dispatching rule when used constantly.
El-Bouri and Shah (Reference El-Bouri and Shah2006) investigate a BNN in order to choose which dispatching rule is to be used in each machine in a job shop system with five machines with the goal of minimizing the makespan and the mean flow time. The authors assign different dispatching rules locally for each machine rather than just one rule common to all. Two NNs are developed in order to optimize each of the performance measurements. Because no learning improvement was achieved with more examples, 2494 examples are generated for the first criterion and 2636 examples for the second one. The proposed technique is compared with three constantly applied dispatching rules on each of the machines. For the criterion of makespan, the NN obtains good results that are very close to being optimal even when the number of jobs is high. The election of the shortest processing time (SPT) or most work remaining (MWKR) rules depends on the number of jobs. For a low number of jobs, the MWKR rule provides better results, whereas for more than 70 jobs, the SPT rule is more appropriate. In the case of mean flow time, the NN also allows less deviation regarding the optimal performance for any number of jobs. In contrast, the SPT rule behaves the worst in the tests, especially during a large number of jobs. The explanation for this anomaly is that the job shop problems applied in this study had a restricted number of job routes.
Mouelhi-Chibani and Pierreval (Reference Mouelhi-Chibani and Pierreval2010) suggest a new approach based on NNs that each time a resource becomes available, it selects, in real time, the most suited dispatching rule. In this case, the weights of the NN are not determined with training examples. Instead, they are determined with an optimization method that uses simulation and SA. In the experimental study, a flow shop system is used with two work centers that are based on a simulation study carried out by Barret and Barman (Reference Barret and Barman1986). The performance criterion that is considered is the mean tardiness. The results attained when the NN, which makes the scheduling decisions, has randomly established parameters are as poor as expected. Once the NN is trained using the proposed approach, the values obtained for the mean tardiness criterion are better than those with the best strategy, which constantly uses the dispatching rules in a percentage higher than 7.28%. In addition, the NN changes the dispatching rules with a high frequency rate; with SPT and EDD being the most selected rules.
Yang and Lu (Reference Yang and Lu2010) propose a hybrid dynamic preemptive and competitive NN approach called advanced preemptive competitive NN method. A preemptive method, which represents the multiple goals as a single objective function, is used for the multiobjective decision. The preemptive method determines a suitable dispatching rule to improve the worst performance from the three performance criteria and to enhance the surrogate objective function of the multiobjective problem. A CNN is used to classify the system conditions into 50 groups. For each group, the dispatching rule for each performance measure is decided by using a brute-force approach. For each production interval, the current system status group is determined by the CNN. The group's corresponding dispatching rules are then used for the preemptive method. In the experimental study, a thin film transistor liquid crystal display manufacturing system is used with two workstations, where three performance criteria are considered: mean cycle time, mean slack time, and throughput. The proposed methodology is compared with a CNN suggested by Min et al. (Reference Min, Yih and Kim1998) and the preemptive method proposed by Chan et al. (Reference Chan, Chan, Lau and Ip2003). The proposed methodology proves to be better than the other two, especially in a bias-weighted multiobject manufacturing environment.
Guh et al. (Reference Guh, Shiue and Tseng2011) have developed a system that assigns different dispatching rules in each of the machines using self-organizing map (SOM) NNs. The proposed system is made up of three main components: a simulation-based training example generation mechanism, a data preprocessing mechanism, and a SOM-based real-time multiple dispatching rules selection mechanism. The data preprocessing mechanism consists of the Las Vegas filter feature selection algorithm (Liu & Setiono, Reference Liu and Setiono1996) and data normalization. The case study involves a modification of the model used by Montazeri and Van Wassenhove (Reference Montazeri and Van Wassenhove1990). At the training example generation phase, 6000 examples are created. The proposed system is compared with two alternatives that use inductive learning (Su & Shiue, Reference Su and Shiue2003) and SVMs (Shiue, Reference Shiue2009a) that use the same dispatching rule in all the machines in each scheduling period. The proposed system demonstrates higher performance in percentages that vary between 6.27% and 0.03%, depending on the performance criterion used.
Shiue et al. (Reference Shiue, Guh and Lee2011) extend the previous work by considering both the input control and the dispatching rule, such as those in a wafer fabrication manufacturing environment (Campbell & Ammenhauser, Reference Campbell and Ammenhauser2000). In the case of the mean cycle time, the levels of progress are between 1.63% and 3%, respectively, with regard to using inductive learning or SVMs. The throughput using the studied methodology is similar but slightly better than the one with the other two techniques.
3.3. CBR-based approaches
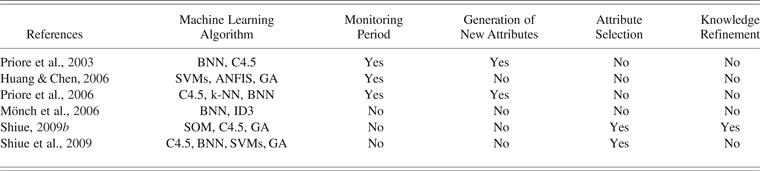
Priore, De la Fuente, Pino, et al. (Reference Priore, De la Fuente, Pino and Puente2001) present a new scheduling technique that uses CBR. In addition, a GA is designed in order to calculate the optimal weights that the nearest neighbor algorithm will need to achieve for the solution. Throughout the experimental study, which uses a FMS (Shaw et al., Reference Shaw, Park and Raman1992), 1100 examples are generated by simulation. The proposed technique is compared with using the C4.5 inductive learning algorithm and when consistently using the dispatching rules with the aim of minimizing the mean tardiness and the mean flow time. The results show that the nearest neighbor algorithm with the optimum weights generates lower mean tardiness values than does C4.5. The combinations modified job due date (MDD) + number in next queue (NINQ) and MDD + work in next queue (WINQ) stand out among the strategies that use a fixed combination of dispatching rules. However, mean tardiness values are higher than the option that uses CBR by between 12.44% and 13.99%. Moreover, the nearest neighbor algorithm and C4.5 obtain similar results, according to the criterion of mean flow time. Furthermore, the combinations SPT + NINQ and SPT + WINQ generate the lowest mean flow time from among the strategies that apply a fixed combination of rules. However, mean flow time values are greater than the C4.5 option by between 4.31% and 4.84%.
3.4. SVMs-based approaches
Liu et al. (Reference Liu, Huang and Lin2005) present a scheduling system that is based on SVMs that allows the most appropriate dispatching rule to be used according to the attributes of the manufacturing system in real time. The case study includes a variation of the model implemented by Montazeri and Van Wassenhove (Reference Montazeri and Van Wassenhove1990). In addition, the measure of performance used is the throughput, and 840 training examples are used. The results indicate that the proposed system achieves better throughput than the other dispatching rules when used constantly. For instance, the throughput with the proposed scheduler is 8.73% better than the one obtained with the best dispatching rules when used constantly, which in this case is the shortest imminent operation time (SIO) rule. In addition, the throughput variance is reduced.
Shiue (Reference Shiue2009a) presents a study that uses SVMs and GAs. This technique is used to determine which of the manufacturing system's attributes are the most important and which parameters suit the SVMs better. The case study concerns an adaptation of the model put in practice by Montazeri and Van Wassenhove (Reference Montazeri and Van Wassenhove1990). The proposed technique is compared with the use of the classical SVMs mechanism. For the throughput and the number of the tardy parts criteria, the results achieved with both techniques are very similar. However, for the criterion of the mean flow time, the use of the classic SVMs system provides results 6% higher than the combination of SVMs and GAs. When comparing the proposed technique with the constant use of a rule, the results obtained for the throughput criterion are proven to be similar. However, for the mean flow time and the number of tardy parts criteria, the constant use of rules produces results approximately 10.52% and 74.49%, respectively, higher than the proposed technique. In addition, the use of this technique provides a better classification performance than the one provided by the classic SVMs system in percentages that vary between 2.57% and 6.98%, depending upon the performance criteria.
Priore et al. (Reference Priore, Parreño, Pino, Gómez and Puente2010) propose a scheduling system that uses SVMs. In the experimental study, a Mazak FMS (Chen & Yih, Reference Chen and Yih1996) and 1100 examples are used with the goal of minimizing the mean tardiness and the mean flow time. The results show that the application of the SVMs, for the mean tardiness criterion, generates values that are 3% lower than the C4.5 algorithm. In contrast, the dispatching rules, used constantly, provide results that are at least 13.96% higher than the SVMs. In addition, for the mean flow time criterion, SVMs and C4.5 provide similar results. Compared with the application of the rules in a constant manner, these provide results at least 4.01% higher than using the C4.5 algorithm.
3.5. Reinforcement learning-based approaches
Wang and Usher (Reference Wang and Usher2004) propose a factorial experiment design for examining the effects of applying Q-learning (a reinforcement learning algorithm) to the single-machine dispatching rule selection problem under different conditions of system loading and due date tightness. The aim of the system is to minimize the mean tardiness. In this study, a single-machine agent dynamically selects one of the three dispatching rules [EDD, SPT, and first in, first out (FIFO)]. The factors examined in this Q-learning application consist of two factors for the agent's policy table and three factors for the reward function. The authors say that when the Q-learning algorithm was used with the recommended factor settings, the learning agent yielded the best performance for one (heavy loading/loose due date) of the four system conditions. However, in each case, the resulting policy derived by Q-learning supported the best rule for the condition. In addition, the authors indicate that more states in the policy table and more ranges for the reward function will increase the learning performance. In contrast, when due dates are tight, the utilization of wider ranges for deciding the states and for establishing penalties resulted in a better performance than when applying narrow ranges. Moreover, it is better to use a higher reward to the action for early jobs.
Wang and Usher (Reference Wang and Usher2005) study the application of Q-learning to a single-machine dispatching rule selection problem to decide if it can be applied to enable a single machine agent to learn commonly accepted dispatching rules for three cases (minimizing maximum lateness, number of tardy jobs, and mean lateness) in which the best dispatching rules have been previously determined (Morton & Pentico, Reference Morton and Pentico1993). In order to evaluate the performance of the learning agent, the authors computed the number of times that each rule was selected during the simulation and then calculated the selection percentages of these rules. The authors say that a machine agent with the Q-learning algorithm is able to learn the best rules for different system objectives.
Yang and Yan (Reference Yang and Yan2009), in order to eliminate the poor effect of a large state space in dynamic scheduling, proposed a B-Q learning algorithm that combines the BSAS algorithm (Theodoridis & Koutroumbas, Reference Theodoridis and Koutroumbas2003) with the Q-learning algorithm. This algorithm produces clusters of the manufacturing system's status, improving upon the learning efficiency and the generalization capability. In the experimental study, the proposed technique is compared with the EDD, SPT, and minimum slack time (MST) rules in a manufacturing cell under the mean tardiness criterion. Different distributions for the processing time of each job are used, and the proposed algorithm shows a reduction in the mean tardiness between 10.61% and 43.34% for the best and worst dispatching rule, respectively. The results also show that the approach outperforms the other three rules when allowance factors with different urgency are taken into account.
Chen et al. (Reference Chen, Hao, Lin and Murata2010) propose a method of developing a composite dispatching rule for multiobjective dynamic scheduling. The approach proposed is based on reinforcement learning and data envelopment analysis. This approach is used to determine dispatching rules that have different strengths on optimizing the objective. The selected rules are subsequently combined into a single composite rule using the weighted aggregation manner. Reinforcement learning is adopted to train the intelligent agent to achieve the knowledge of setting appropriate weight values of elementary rules in composite form in order to cope with the WIP fluctuation of a machine. The proposed scheduling technique is implemented in a job shop system with the goal of minimizing the mean flow time, the mean job tardiness, and a global criterion (Low et al., Reference Low, Yip and Wu2006). The proposed method is compared with two alternative composite rules. In the first, the weights are calculated using the design of experiment and multiple response optimization (Dabbs et al., Reference Dabbs, Fowler, Rollier and Mccarville2003). In the second, the weights are calculated randomly. The authors indicate that the proposed approach has the smallest global criterion value, which proves that it has the best overall performance when compared to the other composite rules. The results also indicate that composite rules have better overall performance than single rules in multiobjective scheduling.
3.6. Mixed approaches
Priore et al. (Reference Priore, De la Fuente, Pino and Puente2003) present a scheduling approach that uses and compares inductive learning and NNs. To improve the manufacturing system's performance, a new approach is also proposed whereby new control attributes that are arithmetical combinations of the original attributes can be determined. In the experimental study, a Mazak FMS is used (Chen & Yih, Reference Chen and Yih1996), and through simulation, 1100 examples are generated. For performance criteria, mean tardiness and mean flow time are used. The generating module is checked to make sure that the new attributes reduce the test errors in both learning algorithms. The results demonstrate that the NN generates lower mean tardiness values than does C4.5. The combinations MDD + NINQ and MDD + WINQ are the best strategies that use a fixed combination of dispatching rules, but their mean tardiness values are higher than the NN alternative by between 11.12% and 11.86%. However, the C4.5 algorithm gives better results than does the NN for the mean flow time criterion. The combinations SPT + NINQ and SPT + WINQ generate the lowest mean flow time from among the strategies that apply a fixed combination of rules. Nevertheless, mean flow time values are greater than the C4.5 alternative by between 4.01% and 4.27%.
Huang and Chen (Reference Huang and Chen2006) propose a scheduling mechanism that combines SVMs, GAs, the theory of constraints, and the adaptive neurofuzzy inference system (ANFIS). GAs are used to look for dispatching rules that provide a performance improvement. The ANFIS prediction model is applied to determine, online, the scheduling interval to be applied. In contrast, the theory of constraints is put forth to determine the appropriate product mix. Finally, SVMs are adopted to determine the dispatching rule to be put into practice at each point in time. The proposed methodology is employed in a wafer fabrication (Wein, Reference Wein1988), with the goal of maximizing the throughput and minimizing the number of tardy jobs. The experimental results show that the proposed mechanism is more effective than constantly using the dispatching rules, in percentages that vary between approximately 8.86% for the throughput criterion and approximately 36.36% for the number of tardy jobs criterion.
Priore et al. (Reference Priore, De la Fuente, Gómez and Puente2006) compare three machine learning algorithms: inductive learning (C4.5), BNNs, and CBR (nearest neighbor algorithm). In the experimental study, an FMS is used (Shaw et al., Reference Shaw, Park and Raman1992), and 1100 examples are generated with two performance measures: the mean tardiness and the mean flow time. To improve the manufacturing system's performance, a new approach is also proposed, whereby new control attributes that are arithmetical combinations of the original attributes can be determined. The results reveal that for mean tardiness, the lowest values are obtained with the nearest neighbor algorithm. These values are lower than those obtained with the NN and inductive learning, and up to 15.21% lower than those provided by the best of constantly applied dispatching rules. In contrast, for the mean flow time, the best results are achieved with the nearest neighbor algorithm and inductive learning, while the values provided with the best constantly applied rules are up to approximately 5% higher than the previous ones.
Mönch et al. (Reference Mönch, Zimmermann and Otto2006) use inductive learning and BNNs in order to determine the appropriate value of the parameter k in the apparent tardiness cost (ATC) dispatching rule applied to scheduling jobs with incompatible job families and unequal ready times on parallel batch machines. The experimental study takes into account the case of three incompatible families and three parallel machines. The results assert that choosing the parameter k via the machine learning approaches leads to high-quality schedules regarding total weighted tardiness. The authors say that the total weighted tardiness can be improved significantly with regards to a fixed k-value approach. In turn, approximately only 1% to 2% of the total weighted tardiness compared to schedules that are calculated by using a nearly optimal parameter k is lost. However, the computational effort is found to be much smaller by following the machine learning approach. Finally, they highlight that the inductive learning based approach slightly outperforms the one that uses the NNs.
Shiue (Reference Shiue2009b) develops a procedure that can automatically modify the scheduling knowledge when important changes occur in the manufacturing system. The scheduling system is made up of five main components: a training examples generation mechanism, a GA-based attribute selection mechanism, a SOM NN to assign labels to each class of the knowledge base, an inductive learning based knowledge base class selection module, and an inductive learning based dynamic dispatching rule selection module. The case study involves a modification of the model used by Montazeri and Van Wassenhove (Reference Montazeri and Van Wassenhove1990). To demonstrate the validity of the proposed technique, 4000 training examples are used, and the results obtained are compared with other classic inductive learning techniques and with the use of constantly applied dispatching rules. A series of experiments are carried out with different combinations of pieces. The proposed method obtains better results than the classic alternative of inductive learning and the constant use of dispatching rules in all the performance criteria. In addition, there are no significant differences between the best dispatching rule that is constantly used and the classic approach of inductive learning owing to the variances that exist in the manufacturing environments.
Shiue et al. (Reference Shiue, Guh and Tseng2009) have developed a technique that consists of two modules: a GA and a classifier that can be used with three learning algorithms: BNNs, inductive learning (C4.5), and SVMs. The proposed GA can search for the best learning algorithm and, simultaneously, determine the ideal subset of system attributes and learning parameters. In the experimental study, the FMS used is a modification of the model used by Montazeri and Van Wassenhove (Reference Montazeri and Van Wassenhove1990). Four thousand training examples are used, and results are obtained with the three classifiers that were previously mentioned, based on three performance measures: throughput, mean cycle time, and number of tardy parts. The results show that the C4.5 algorithm obtains the best results for the throughput criterion, while the SVMs are the best for the other two performance criteria.
3.7. Other approaches
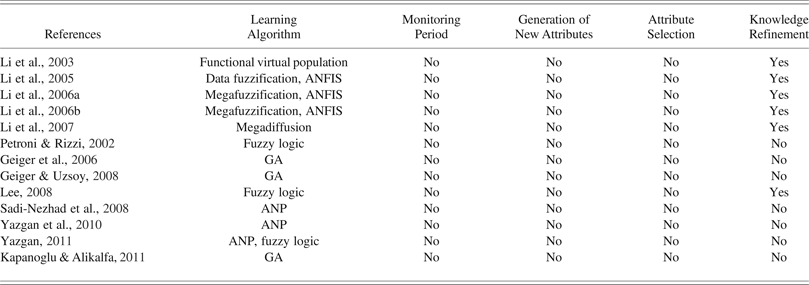
In the early stages of an FMS, only a small amount of data is obtained, and this means that the scheduling knowledge is often not very reliable. In order to fix this problem, Li et al. (Reference Li, Chen and Lin2003) proposed an approach called “functional virtual population.” This algorithm was developed in order to expand the domain of the system attributes and to create a number of virtual samples that would make a more robust scheduling knowledge base. The authors use three simple search strategies: right searching, left searching, and mixed searching. In the experimental study, an FMS is used, and in order to obtain scheduling knowledge, a BNN is used. With the 20 original examples, the learning accuracy of the network is 32.75%. When the proposed approach is applied, the accuracy is 65.5% with only 40 training examples.
Li et al. (Reference Li, Wu, Tsai and Chang2005) use the data fuzzifying concept as an alternative to expand the early data set and ANFIS. The proposed methodology is used in an FMS as applied in Li et al. (Reference Li, Chen and Lin2003), and it is compared with a traditional NN. The results show that the fuzzy learning technology is better than the traditional crisp learning approach. More specifically, the learning accuracy obtained by using a traditional NN is increased from approximately 51%, for size 5 data sets, to approximately 78%, for sets containing 100 pieces of data. In contrast, the accuracy provided by the proposed method is increased from approximately 79% to approximately 93%. In addition, the authors indicate that enlarging the data domain to a reasonable range can prevent the bias of limited data and improve learning accuracy.
Li, Wu, Tsai, et al. (Reference Li, Wu, Tsai and Chang2006) tried to improve upon the prior work (Li et al., Reference Li, Wu and Chang2005), which demonstrated three flaws. In the first place, the possible attribute domain range must be predetermined. In addition, the domain range expansion is essentially a trial and error procedure. Finally, the domain range expansion does not consider data behavior (trend). In order to solve these issues, the authors put forth combining data fuzzification, data trend estimation, and ANFIS to improve FMS scheduling accuracy. In addition to the latter, this research proposes a procedure, called asymmetric domain range expansion, to estimate the data trend, while expanding the data domain ranges. The experimental results show that the learning accuracy with this methodology ranges from approximately 69.3%, for sets of 5 pieces of data, to approximately 94.7%, for size 100 data sets. The results are similar to those obtained by Li et al. (Reference Li, Wu and Chang2005), but they require less computational time.
Li, Wu, and Chang (Reference Li, Wu and Chang2006) also searched for a quantitative method to determine the range of domain external expansion under unknown domain bounds using the learning error ratio as the data bandwidth ratio (Anthony & Biggs, Reference Anthony and Biggs1997). In addition, the mean and median are used to identify the direction and degree of the data bias. In the experimental study, the proposed method is checked to ensure that better results are obtained, especially when the size of the data set is under 20.
Finally, Li et al. (Reference Li, Wu, Tsai and Lina2007) use a methodology that combines megadiffusion and data trend estimation, called “megatrend diffusion,” in order to estimate the range of small data sets and to produce artificial samples in order to train a modified BNN. In this study, unlike the conventional way of diffusing each sample individually (Huang & Moraga, Reference Huang and Moraga2004), the megadiffusion method diffuses a set of data using a common diffusion function. In the experimental study, the authors compared training data sets ranging between 5 and 100 pieces of data. The learning accuracy increased from 78.23% to 95.33%. Compared to Li, Wu, Tsai, et al. (Reference Li, Wu, Tsai and Chang2006), it is obvious that this research has higher learning accuracy when the training data size is below 40.
Petroni and Rizzi (Reference Petroni and Rizzi2002) propose a fuzzy logic based tool intended to rank flow shop dispatching rules under multiple performance criteria. The authors indicate that because the suitability of a specific rule, as well as the relative importance of performance criteria, are easily determined by experts through linguistic judgments, a method to multiattribute decision making in an ill-defined environment might be given by a fuzzy logic approach. The method is illustrated by a real case application to a flow shop firm operation in the boilermaker line of business. Three criteria, three decision makers, and five dispatching rules are used. The first step is to value the relative weights of the criteria. The second step is to assess the effects of the adoption of each dispatching rule in the performance criteria. The third step is then to calculate the fuzzy suitability index for each dispatching rule. The authors provide the following ranking for the rules: cost over time (COVERT), SPT, slack per remaining operation (S/OPN), EDD, and FIFO.
Geiger et al. (Reference Geiger, Uzsoy and Aytug2006) propose a technique that is capable of automatically discovering effective dispatching rules. The proposed system, scheduling rule discovery and parallel learning system (SCRUPLES), uses an evolutionary learning mechanism with a simulation model, thereby automating the process of examining different rules and using the simulation to assess their performance. The authors say that the technique is evaluated in a variety of single machine environments and discovers rules that exhibit similar, if not better, performance than the rules reported in the literature, which are the results of decades of research. Following this, Geiger and Uzsoy (Reference Geiger and Uzsoy2008) used SCRUPLES for several batch scheduling environments. Once again, SCRUPLES generates dispatching rules that are competitive with those presented in the literature.
Lee (Reference Lee2008) uses a fuzzy rule based system that dynamically selects the most appropriate rule according to the current state of the manufacturing system. The distributed fuzzy sets approach, which uses multiple fuzzy numbers simultaneously, is used to recognize the system states. The author indicates that the proposed approach consists of two phases. The knowledge acquisition phase has three steps: (1) selecting and fuzzifying the state variables, (2) collecting the performance of possible rules for each state vector from the results of simulation and feedback of real decision making, and (3) building and updating a rule base by calculating suitability of the rules for each state vector. The decision-making phase assesses the appropriateness of candidate rules for the given state vector and uses the most appropriate dispatching rule. In the experimental part, a hypothetical FMS is used and the mean flow time is applied as the performance criterion. The proposed methodology is compared with the constantly applied dispatching rules and with a system that is based on BNNs. The proposed scheduling system is checked to make sure that it provides better performance than the previous methods, with percentages varying between 0.1% and 11.05%, depending on the considered environment.
Sadi-Nezhad et al. (Reference Sadi-Nezhad, Didehkhani and Seyedhosseini2008) developed a fuzzy analytical network process (ANP) model in order to choose the best dispatching rule in an FMS. The authors indicate that in most conditions there are certain internal dependencies among criteria; therefore, they cannot use the analytical hierarchical process. In this study, three dispatching rules and three criteria are used for scheduling an FMS. In addition, the approach of Mikhailov (Reference Mikhailov2003) is used for deriving priorities from a fuzzy pairwise comparison matrix. Results indicated that the model can be applied easily by managers, and they can revise the model to consider future systems and environment changes.
Yazgan et al. (Reference Yazgan, Boran and Goztepe2010) also propose an ANP model that has a multicriteria structure and consists of most of the companýs manufacturing systems parameters (criteria) and the company's macrostrategies. Owing to the existence of interactivities among criteria, a choquet integral approach (Yang et al., Reference Yang, Chiu, Tzeng and Yeh2008; Tseng et al., Reference Tseng, Chiang and Lan2009) is used. The ANP model is applied to an FMS and consists of four main criteria (benefit, opportunity, cost, and risk), three criteria (customer, economic, and strategy), a different number of subcriteria for each criterion (46 subcriteria in total), and 10 different dispatching rules as alternatives. The authors indicate that the best rules are in the order EDD, SPT, and critical ratio (CR). Later, Yazgan (Reference Yazgan2011) proposed an ANP model in which the fuzziness of information was also considered during the evaluation process. In addition, the extent analysis method of Chang (Reference Chang1996) was used for the pairwise comparisons. In the experimental study, similar to the previous study (Yazgan et al., Reference Yazgan, Boran and Goztepe2010), the authors indicate that the best rules are in the order SPT, EDD, CR, and COVERT.
Kapanoglu and Alikalfa (Reference Kapanoglu and Alikalfa2011) propose a scheduling system that uses GAs to create decision rules. These rules are based on the queue lengths of the machines in order to determine the most appropriate dispatching rules at each moment in time. In this case, the experimental study is carried out on a job shop system with the goal of minimizing the total tardiness, for a different number of jobs and due date tightness. The results prove that the proposed technique gets better results than the best dispatching rules in every one of the scheduling problems proposed. The scheduling system shows an enhancement that fluctuates between 0.29% and approximately 44.80% with regard to the best constantly used dispatching rules. Even when using two or three intervals for the queue (the most basic structure of the approach), the improvement is between 0.29% and 34.25%.
4. DISCUSSION AND FUTURE RESEARCH
A number of limitations that would be desirable characteristics can be detected across the board in the approaches considered above. These limitations refer to future research directions in the field of dynamic scheduling of manufacturing systems, by modifying the dispatching rule that is used. Future research directions would include:
1. Determination of the optimum number of training examples: There are very few approaches that calculate the number of examples required to optimally train the machine learning algorithm. Nor do they specify whether the test examples are the same, similar, or very different to the training examples. Yet the scheduling knowledge classification error, and consequently the performance of a manufacturing system, depends greatly on the number of training examples considered. It is therefore necessary to study the classification error as a function of the number of examples considered, and hence, an adequate size of the training set must be chosen.
2. The use of CBR as a machine learning methodology in scheduling systems: Despite their simplicity, these algorithms are very efficient at classifying (Rachlin et al., Reference Rachlin, Kasif, Salzberg and Aha1994). Except in the work of Priore, De la Fuente, Pino, et al. (Reference Priore, De la Fuente, Pino and Puente2001), there are hardly any others using this methodology.
3. Selection of an adequate monitoring period: A study to determine the right monitoring period for each performance criterion is not generally covered in the existing literature. However, the frequency of control attribute checking, to be able to decide whether dispatching rules are to be changed or not, is a very important question that will determine the manufacturing system performance.
4. Generation of new control attributes using an algorithm that can create attributes that are a combination of the initial ones: However, these combinations are not often known at the outset and can only be discovered in simple manufacturing systems after detailed examination of the simulation results. Again, there are very few approaches that determine new control attributes.
5. Selection of the control attributes: Because essential attributes are uncertain in manufacturing systems, the selection of optimal subsets of manufacturing attributes to enhance the generalization ability of knowledge bases and to avoid overfitting is an extremely important topic that few authors have studied.
6. Comparison of the different machine learning methodologies: The approaches described in the literature use, in most of the cases, a methodology or, in certain cases, a combination of methodologies. However, there are hardly any comparative studies that determine which method is the best.
7. Refinement of the knowledge base: Once developed, the knowledge base is not static, so it would be interesting to establish a procedure that would automatically modify knowledge if important changes in the manufacturing system occur. The main goal of the refinement module is to discover deficiencies in the knowledge base and add training cases that cater to them.
One of the greatest problems, when it comes to comparing the approaches reviewed, is the lack of benchmark problems, which makes this comparison very difficult. Each author uses different manufacturing systems with different job characteristics and different performance criteria. However, according to Priore et al. (Reference Priore, De la Fuente, Gómez and Puente2006) and Shiue et al. (Reference Shiue, Guh and Tseng2009), SVMs and CBR are the best machine learning algorithms, followed by inductive learning algorithms as the second best option, and finally neuronal networks have the worst performance. Nevertheless, the great advantage of inductive learning, regarding the rest of machine learning algorithms, is that the knowledge obtained is intelligible, which could be very useful.
The four above-mentioned machine learning algorithms require a set of examples to be able to learn. In the works of Li et al. (Reference Li, Chen and Lin2003, Reference Li, Wu and Chang2005, Reference Li, Wu and Chang2006, Reference Li, Wu, Tsai and Chang2006, Reference Li, Wu, Tsai and Lina2007), the problem is solved when there are sets of examples with very few data. Nevertheless, reinforcement learning based approaches do not need a set of examples because they learn by directly interacting with the system (its environment) and responding to the reception of rewards or penalties based on the impact of each action on the system. In general, the pros and cons of the reviewed knowledge based scheduling systems correspond with those of the machine learning algorithm used in each case. This is because the framework of the different scheduling systems is very similar, except for the machine learning algorithm used.
In contrast, the approaches applying ANP (Sadi-Nezhad et al., Reference Sadi-Nezhad, Didehkhani and Seyedhosseini2008; Yazgan et al., Reference Yazgan, Boran and Goztepe2010; Yazgan, Reference Yazgan2011) or fuzzy logic (Petroni & Rizzi, Reference Petroni and Rizzi2002) carry out a classification of the dispatching rules with a greater amount of information than the rest of the approaches reviewed. However, the authors do not use them to carry out dynamic scheduling. Finally, it is worthwhile pointing out that an alternative manner of comparing the different approaches is observing the characteristics of each one of them in Tables 1–6. It is to be expected that those approaches with a greater amount of desirable characteristics (monitoring period, generation of new attributes, attribute selection, and knowledge refinement) will also have a better performance.
Table 1. Characteristics of inductive learning based approaches

Note: C4.5, an inductive learning algorithm; GA, genetic algorithm, SA, simulated annealing; ID3, a learning algorithm.
Table 2. Characteristics of neural network based approaches

Note: CNN, competitive neural network; BNN, backpropagation neural network; GA, genetic algorithm; NN, neural network; SA, simulated annealing; SOM, self-organizing map.
Table 3. Characteristics of case-based reasoning and SVM based approaches

Note: SVM, support vector machine; k-NN, k-nearest neighbor algorithm; GA, genetic algorithm.
Table 4. Characteristics of reinforcement learning-based approaches

Note: Q-learning, a reinforcement learning algorithm; B–Q-learning, a combination of the basic sequential algorithmic scheme algorithm with the Q-learning algorithm; DEA, data envelopment analysis.
Table 5. Characteristics of mixed approaches

Note: BNN, backpropagation neural network; C4.5, an inductive learning algorithm; SVM, support vector machine; ANFIS, adaptive neurofuzzy inference system; GA, genetic algorithm; k-NN, k-nearest neighbor algorithm; ID3, a learning algorithm; SOM, self-organizing map.
Table 6. Characteristics of other approaches

Note: ANFIS, adaptive neurofuzzy inference system; GA, genetic algorithm; ANP, analytical network process.
5. CONCLUSIONS
This paper provides a review of the literature on dynamic scheduling of manufacturing systems using machine learning. A classification of general approaches found in the literature is provided. Several knowledge-based approaches that dynamically modify the dispatching rule being used at a specific instance are reviewed depending on the machine learning algorithm used. Next, we indicate a number of limitations that would be desirable characteristics, which are lacking in most approaches we have reviewed. Finally, the point is made that in future work, it would be interesting to design a scheduling module that would incorporate the seven characteristics listed and measure the effect of each of them on the performance of scheduling systems.
Paolo Priore received a degree in industrial engineering in 1991 at the University of Oviedo and a PhD from the University of Oviedo in 2001. He is currently a Professor at Gijón Polytechnic School of Engineering. His research interests include machine learning applications in production problems, simulation, and manufacturing. He has published numerous research papers in a number of leading journals.
Alberto Gómez received a degree in industrial engineering in 1993 at the University of Oviedo and a PhD from the University of Oviedo in 2001. He is currently a Professor at Gijón Polytechnic School of Engineering. His research interests include applications of GAs in production problems and information systems. He has published numerous research papers in a number of leading journals.
Raúl Pino received a degree in industrial engineering in 1992 at the University of Oviedo and a PhD from the University of Oviedo in 2000. He is currently a Professor at Gijón Polytechnic School of Engineering. His current research interests are in artificial intelligence, forecasting, and manufacturing. He has published numerous research papers in a number of leading journals.
Rafael Rosillo received a degree in informatics engineering in 2008 at the University of Oviedo. He is currently an Assistant Professor at Gijón Polytechnic School of Engineering. His current research interests are in artificial intelligence, forecasting, and economy. He has published research papers in leading journals.