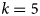Introduction
The design of industrial parts typically consists of re-using, configuring, and assembling existing components, solutions, and knowledge. Indeed, it has been suggested that more than 75% of design activity comprises the re-use of previously existing knowledge (Hou and Ramani, Reference Hou and Ramani2004). Despite this one of the primary reasons why companies still struggle to perform projects on time and budget is the lack of knowledge re-use, which leads to frequent reinventing the wheel rather than finding, and using, already known solutions (Schacht and Mädche, Reference Schacht and Mädche2013). Similarly, Bracewell et al. (Reference Bracewell, Wallace, Moss and Knott2009) argue that only 20% of design information is re-used despite 90% of all design activities being based on the variants of existing designs. Aware of these statistics researchers have suggested that one of the significant difficulties constraining levels of design re-use is the generation of design solutions that partially re-use previous designs to satisfy new requirements (Smith and Duffy, Reference Smith and Duffy2001). Although 3D search technologies have been increasing in capability and retrieval speed for over a decade [e.g., Search by sketch (Liu et al., Reference Liu, Luo, Joneja, Ma, Fu and Song2013), Search by gross shape (Corney et al., Reference Corney, Rea, Clark, Pritchard, Breaks and MacLeod2002), and Search by feature (Jiang et al., Reference Jiang, Chen and He2013)], they have not found widespread commercial application.
Consequently, even with effective 3D search tools, a designer still has to manually assess and edit 3D CAD models to facilitate re-use of specific geometric features they incorporate. It can also be observed that systems for contents base retrieval from CAD databases are more widely reported for global, rather than partial, shape matching (Ip and Gupta, Reference Ip and Gupta2007). Although the search algorithms are quicker, one drawback that remains with 3D search systems is that retrieval results can hugely vary for incomplete and vague queries, subjectivity differences of the similarity measure, inappropriate representation and understanding of user search intent, and rigid similarity check does not always yield retrieved parts that are appropriate for re-use.
In contrast, the interactive predictive design interface envisaged by this research should allow engineers to more effectively design new components that incorporate established, or standard, functional and previously manufactured geometries. In this way, the system would prompt the users with fragments of 3D components that complete or extend, geometry defined by the user. The need for Intelligent Design Assistant (IDA) for design re-use has been widely emphasized in the engineering design literature (Duffy and Duffy, Reference Duffy and Duffy1996). The vision in the presented research work is to produce a 3D design support system that is analogous to the predictive text message systems of mobile phones (which complete words or phrases by matching fragments against dictionaries, or phrases, used in previous messages). Such a system could potentially increase design productivity by making the re-use of established designs a natural and effortless part of the engineering design process.
The CAD re-use systems reported in the literature (Chaudhuri et al., Reference Chaudhuri, Kalogerakis, Guibas and Koltun2011) often need substantial preprocessing time with some algorithms requiring manual data labeling. However, the recent appearance of new subgraph match algorithms (Sun et al., Reference Sun, Wang, Wang, Shao and Li2012) has raised the possibility of feature-based retrieval from industrial-scale datasets (e.g., 10,000–100,000 parts) at interactive speeds (Paterson and Corney, Reference Paterson and Corney2016). Using such an approach, the activity of a designer using a CAD system would continuously generate queries and propose re-use options. The interface challenge lies in controlling the extent and volume of matches returned by the method.
This research investigates how effectively computational models are able to predict the occurrences of specific types of shape features that commonly occur in a family of product models. The work presented seeks to answer the research question:
Which of the three predictive methodologies investigated (i.e. sequential, machine learning or probabilistic methods which use N-Grams, Neural Networks (NN), and Bayesian Networks (BN) as representative of these methods) produce the best performance for the hole and boss type features commonly used in families of hydraulic valves?
To answer this question, a dataset of 3D component models are represented as a set of unordered feature parameter values, specifically the diameters of circular hole or cylindrical boss features. Various forms of frequency distributions generated from this data are then used in a number of different prediction algorithms. The results compares the prediction accuracy of three types of probability model: N-Grams, Bayesian networks, and Neural networks. The challenge addressed in using these prediction approaches is in constructing a representation of the data that allows accurate predictions.
Like many other complex algorithms, the authors anticipate that the predictive model used by a CAD system will be invisible to the users. The results only being manifested in the user interface by the choice and ordering of parameter values in specific feature creation operations. For example, the output of a model predicting the most likely choice of feature dimensions using bi-grams might be made available to the user via a pop-up selection list during a CAD modeling operation. Figure 1 shows the predicted “next” hole suggestions (on the bottom box) in response to the creation of a previous hole feature.
Fig. 1. Hole menu whose values and order are generated by a predictive model.
The rest of this paper is structured as follows: Section “Predictive CAD state-of-the-art” presents a survey of the predictive CAD literature. The reported systems are classified in terms of eight characteristics, before the representation of the CAD models, the algorithms used for prediction and the methods employed for performance assessment are discussed. Having established the context, Sections “Aims, objective, and methodology” and “Probability models” describe the authors’ objectives and the methodology adopted in terms of design representations, the implementation of the probability models and assessment. Section “Assessment of predictive performance” describes the features associated with a dataset of hydraulic valve bodies retrieved from an online CAD archive of commercial designs used in the investigation and presents a comparison of the prediction methods. A predictive CAD software prototype is introduced in the section “Prototype implementation and evaluation,” and possible extensions to the modeling approaches discussed in the section “Extending the predictive models.” The significance of the modeling results are discussed in the section “Discussion” before conclusions are made and further-work outlined.
Predictive CAD state-of-the-art
The phrase “Predictive CAD” is assumed in this paper to refer to support-systems that an engineer would use during CAD modeling by providing suggestions that are appropriate to the current state of an ongoing design defined by a 3D model. Such a system aims to reduce modeling time, increase creative ability by enhancing the exploration of existing CAD models, and improve the productivity of designers.
Although the size of commercial CAD archives and the availability of data-mining tools are making Predictive CAD increasingly feasible, investigations have been reported in the literature since the 1980s. For example, Jakiela (Reference Jakiela1989) published a suggestion-making CAD system that uses a feature-based representation of the design and a production rule representation of the concurrent engineering knowledge. For specific products (where design rules are well understood), suggestion systems known generically as “product configurators” are well established.
In contrast to these systems, where the design rules are manual coded, the author's aim is for a Predictive CAD system where the “rules” for feature suggestions are only defined implicitly in the shapes of CAD models. In other words, the work reported here is a product-based predictive system which focuses on generating component suggestions by extracting semantic and geometric understanding of the features incorporated in CAD models.
Table 1 summarizes the previous research on predictive CAD systems. The following subsection discusses this literature and puts the authors’ work in context.
Table 1. Predictive CAD research papers in the solid CAD modeling literature
The literature reviewed suggests that the development of predictive design systems have four essential steps, namely: definition of the predictive problem, preprocessing of CAD models, algorithms for selecting CAD suggestions, and validating the proposed predictive system. Each of these is now considered in turn.
Characterizing predictive design systems
Regardless of the many differences, the predictive CAD systems literature can be classified by eight characteristics of their functionality and architecture:
1. Source of Experience: Focus or Unfocused: Focus is analogous to a “search” operation, where the user knows precisely, or approximately, what CAD models are relevant to a design. Some inputs may be expected from the user. Whereas, unfocused is an exploration process, in which the user discovers new possible CAD models that can be used in designing. No input is required from the user.
2. Scope of Functionality: Domain Dependent or Independent: Domain dependent focuses on creating suggestions only from a specific type of product (e.g., chair). Whereas domain independent concentrates on creating suitable suggestions from various ranges of products (e.g., chair, desk, wardrobe).
3. Style of Learning: Supervised or Unsupervised: In supervised prediction, a mapping is carried out between the input (i.e., the current design state) and the output (i.e., generated suggestions) using the training CAD dataset. In unsupervised prediction, no predefined mapping is established before the algorithm automatically extracts the required structure in the given CAD dataset with reference to the current design state to generate suggestions.
4. Extent of Locations: Single-point or Multi-point suggestions: In the single-point approach, suggestions are consecutively provided for one particular area of the current design. Whereas the multi-point approach provides recommendations across many regions of the current model simultaneously.
5. Completeness of Shape: Feature or Component suggestions: The feature suggestions will focus on some specific geometric or topological properties of a part. The component suggestions will focus on complete addition of a component to the current design.
6. Scope of Sequences: Immediate or Subsequent suggestion level: Immediate suggestion systems focus on proposing the next step in a design process. But, subsequent suggestion systems aim to suggest multiple steps in the design process.
7. Scope of Motifs: Presence or Occurrence patterns: In presence, a suggestion is provided for incorporation of a feature, or component, once in the current design. Whereas occurrence provides a recommendation plus a form of multiplier so recurrent patterns of arrangement (e.g., a bolt circle) could potentially be added to the current design state.
8. Scope of Inference: Geometric and Semantic suggestion: Geometric suggestion will be purely based on the shape structure. The semantic recommendation will be based on considering the underlying meaning surrounding the current shape structure.
Supplementary Material S1 summarizes the reported predictive design systems in terms of these eight characteristics. The classification reveals that the current literature is dominated by component based, multi-point suggestions that are derived from both the geometry of CAD models and the semantics of associated information. The other characteristics are found with roughly equal frequencies in the other reported work. Defining predictive CAD system in terms of these characteristics will be useful for subsequent development steps such as establishing information requirements, identifying algorithms for prediction, and developing an appropriate user interface for the CAD system.
Design representation
Information extracted from CAD models is essential for all the predictive mechanisms reported. Three types of methods are used to extract data from CAD models to characterize the structure of shapes for use in predictive CAD system: Labeled, Semi-labeled, and Unlabeled.
In the Labeled method, all components are annotated with text that provides a semantic understanding of the design's structure. In the Semi-labeled approach, text annotation is only used at the training stage, but not at the testing stage. The Unlabeled method only uses geometric information for generating predictive suggestions. The unlabeled approach is preferred because significant checks are required in the labeled method to verify that the labels generated are appropriate for the geometric structures they are applied to. Also, the availability of annotated CAD model datasets is limited. However, in the reviewed literature, there are only four predictive CAD systems that focused solely on the unlabeled approach. Since this work focuses on the unlabeled approach, the reported research related to this approach are summarized and discussed in the following paragraphs.
Component segmentation is a common preprocessing step that enables an understanding of potential geometric and functional compatibility with other components considered by a predictive support system. Chaudhuri and Koltun (Reference Chaudhuri and Koltun2010) proposed a geometric approach to segmenting an object by using a Shape diameter function and an approximate “convex decomposition” approach. In addition to segmentation, Jaiswal et al. (Reference Jaiswal, Huang and Rai2016) used light-field shape descriptor for manipulating shape similarity, and principal component analysis for sizing and scaling. Li et al. (Reference Li, Xu, Chaudhuri, Yumer, Zhang and Guibas2017) presegmented objects into constituent parts, and defined their spatial arrangements by oriented bounding boxes, represented as a fixed-length code that defined the geometry and grouping mechanism (connectivity or symmetry). Sung et al. (Reference Sung, Su, Kim, Chaudhuri and Guibas2017) did not rely on consistent part segmentations; instead, they constructed contact graphs over the components, which can be partitioned in various ways to create training pairs of a partial assembly.
Although the above approaches provide directions for preprocessing CAD models, there are still difficulties involved in consistent segmentation, prealignment of objects, scaling objects, object categorization, and relationship identification (e.g., adjacency and repetition). The creative and adaptive part segmentation is essential for predictive CAD because the suggestions need to be available in situ with reference to the designer's initial drawings. Unlike the 3D solid models, where segmentation is required to extract components, the feature-based predictive CAD system required the extraction of features such as holes and slots.
Probability models
The two essential elements in assembly-based predictive algorithms are to (1) establish relationships between components and (2) generate a ranking for suggestions. The approaches used for this are summarized in Figure 2. In unlabeled methods, Chaudhuri and Koltun (Reference Chaudhuri and Koltun2010) used 
$\text {D}^3$ (descriptive–descriptive–distance) histogram signatures to encode a shape's global spatial structure and its local detail to identify suggestions for the given shape query. An averaged correspondence score from sample points in the database was calculated to identify the likelihood of an object having a counterpart for the query, which also has a similar gross structure to the query. Jaiswal et al. (Reference Jaiswal, Huang and Rai2016) used the marginal probability distribution computed from a “factor graph,” which incorporates adjacency and multiplicity factors of segmented components, to score and rank the predicted components. The adjacency factors include shape similarity information with the assumption that parts that have similar adjacent components are more likely to appear next to each other. The conditional probability for latent variables was computed as the product of all the factors divided by normalizing constant.
Fig. 2. Learning approaches used in reported predictive CAD systems.
Sung et al. (Reference Sung, Su, Kim, Chaudhuri and Guibas2017) and Li et al. (Reference Li, Xu, Chaudhuri, Yumer, Zhang and Guibas2017) used supervised and unsupervised neural network architectures for generating predictive suggestions, respectively. Sung et al. (Reference Sung, Su, Kim, Chaudhuri and Guibas2017) proposed embedding and retrieval neural network architectures for suggesting complementary functional and stylistic components and their placements for an incomplete 3D part assembly. These two networks were tightly coupled and trained together from triplets of examples: a partial assembly, a correct complement, and an incorrect complement. A mixture of Gaussians with confidence weights (conditional probability distribution) was used to train the network to predict a probability distribution over the space of part embedding. Li et al. (Reference Li, Xu, Chaudhuri, Yumer, Zhang and Guibas2017) developed a recursive neural network that encodes and decodes shape structures via discovered symmetry hierarchies (i.e., translational, rotational, and reflective symmetry) in an object class. The network encodes the structure and geometry of the oriented bounding box (OBB) layouts of varying sizes into fixed-length vectors, and then learns by recursively assembling a set of OBBs into a fixed-length root code and then decodes the root to reconstruct the input. The network was assessed by minimal-loss code that considered both geometry and structure in the decoding process.
Variations in the types of information available have necessitated different approaches to predicting what component suggestions will be most appropriate. Chaudhuri and Koltun (Reference Chaudhuri and Koltun2010) used shape histogram signature to calculate a correspondence score between the query and the dataset model. Whereas Jaiswal et al. (Reference Jaiswal, Huang and Rai2016) used a factor graph to include adjacency and multiplicity factors in the prediction pattern. Sung et al. (Reference Sung, Su, Kim, Chaudhuri and Guibas2017) illustrated the neural network approach using the point cloud representation of the component and Li et al. (Reference Li, Xu, Chaudhuri, Yumer, Zhang and Guibas2017) used OBBs to represent the spatial arrangements of parts. In contrast to the algorithms for component selection presented in the literature, the predictive problem addressed in this paper is focused on features and specifically the identification of the next feature's parameter value, within specific feature type, which the user can add to a component during an ongoing design process. Despite the differences in the size and variety of the search space, the preceding review has provided some useful insights. For example, the literature suggests that a learning algorithm should minimize the number of variables used to represent a component's structural variability and spatial relationships and also that a predictive model should provide generalization and avoid overfitting of the training data.
Validation of predictive systems
Figure 3 lists the assessment criteria used for evaluating predictive systems. The parameters used for evaluation in the literature vary and consequently it is not feasible to carry out a comparative study of the reported predictive systems. Among the four unlabeled approaches, only Jaiswal et al. (Reference Jaiswal, Huang and Rai2016) reported the percentages of relevant predictions which varied from 85% to 91% for the top 10 to 50 component suggestions (with experiments repeated for five different component configurations in each product domain).
Fig. 3. Evaluation parameters reported for predictive systems.
The predictive CAD literature largely focused on predicting components for assemblies using 3D solid models. In contrast, this research work focused on feature-based predictive CAD system using B-rep models. In summary, the literature suggests that an ideal predictive CAD systems should require minimal preprocessing activities (e.g., model orientation and scaling) and avoid computational intensive processes so large numbers of designs can be quickly compared. Also, the rational for suggestions should also be easily comprehensible by users (e.g., a clear mapping between query and suggestions) and should be integrated into novel use interface designs that do not intrude or distract from the design process.
Aims, objective, and methodology
Given the research vision presented in the introduction and the work reported in the literature survey, the research aims are:
1. To define a computational architecture for valve body design that takes as its inputs the current state of an ongoing design and a databases of previous designs and outputs a list of the diameter values of the hole and boss features most likely to be added next.
2. Identify the best probability model to adopt for a specific dataset of mechanical designs.
To realize these aims, the following objectives were identified:
1. Establish methodologies and benchmarks for the creation and performance measurement of a predictive CAD systems.
2. Use the methodology to quantify the performance of three different probability models.
Methodology
A synthesis of the work reported in the literature survey was used to define a generic six-step approach to the development of a predictive CAD system illustrated in Figure 4. The process starts by defining the predictive problem using eight defined characteristics identified in the section “Predictive CAD state-of-the-art.” This dictates the information required for prediction, the approaches needed to extract that information, and the development of the probabilistic model employed to generate the predictions. The final two steps will be to integrate the probabilistic model with an appropriate user interface to evaluate the benefits of the predictive system and to refine with further development. In this research, the feature prediction problem is defined by the following parameters: unfocused, domain dependent, supervised, multi-point suggestion, immediate suggestion level, presence, and semantic suggestion. The rationale for choosing these parameters were to enable an explorative, rather than defined, feature search and to be specific in this first stage of feature-based predictive development system.
Fig. 4. Generic predictive CAD development steps mapped to the specific implementation used for evaluation of probability models.
The prediction approach represents each component in the database as a sequence of unordered sets of unique features. Each feature in the set is represented by an alphanumeric symbol composed of a code for the feature type and the values of its design parameters (i.e., dimensions). For example, Figure 5 shows a component whose feature content is represented as a set of alphanumeric symbols: {h10, h12, h14, h75, h45, b110, b90, b110} that is independent of the local geometry or relative locations (e.g., adjacent or intersecting).
Fig. 5. Component feature content representation.
The feature prediction system is modeled as a supervised learning problem in which features are revealed sequentially in response to the input features. Thus, the problem definition in this work is similar to an online grocery store system which suggests the next item to put in the cart (Letham et al., Reference Letham, Rudin and Madigan2013). In other words, the predictive CAD problem is framed to sequentially predict subsequent features from the given set of feature(s). The number of input features can vary from one to many and do not have to be in the created order. The feature prediction process is structured based on the number of input features.
To assess the presented methodology, the performance of three different probability models using a database of component features extracted from a collection of mechanical valve bodies; these components are dominated with holes and cylindrical bosses features (used to locate bolts to secure different components together as well as other, functional holes that are used for liquid flow, pressure release plug connector, valve controller stem, and bonnet gasket connections). So if a designer chooses the size of a bore hole diameter to, say, maximize fluid flow, the proposed predictive CAD system will subsequently suggest other functional holes using the patterns of hole sizes that are observed to frequently co-exist in the CAD database.
A sample of the feature sequences extracted from components in the dataset are listed in Table 2. We denote the set of 
$p$ distinct features present across the component designs with 
$X$. There are 
$N$ valve components and each component is represented by an unordered collection of features which we denote 
$S = { S_i} _{i\in { 1, \ldots , N} }$ and each distinct feature type within the collection we denote with 
$f_x,\; x \in { 1,\; \ldots ,\; p} ,\; f_x \subseteq X$. For example, an existing set of features found in the database could be 
$S_1 = { h10,\; h12,\; h14,\; h75,\; h45,\; b110,\; b100,\; b90}$ with a distinct feature 
$f_1 = { h10}$. As the designer develops a design by adding features, a set of recommendations can be provided based on patterns emerging among the features in the existing CAD database. That is, for a new design 
$S_{i + 1}$ with existing features 
$O = { f_1,\; f_2}$, a set of recommendations for the next feature, 
${ f_x} _{\vert { f_x} \vert \le ( p-\vert o\vert ) }$, are provided based on the conditional probability of 
$f_x$ given 
$O$, estimated from the sequence frequency in the existing database. The generation of predictions can proceed sequentially as more features are included.
Table 2. An illustration of feature data extracted from components
Probability models
This section describes the data input, the three prediction methods that were used to estimate the conditional probabilities, and the method of evaluating predictive performance. Figure 6 illustrates the procedure that was followed in this analysis to convert the features present in CAD model designs into a predictive system; lists of features extracted from CAD models can be transformed into a binary matrix which can then used as the input to each probability model. This process would support product families that have common sets of features.
Fig. 6. Model assessment methodology.
Model input
The extracted lists of hole and cylindrical boss features were transformed into a binary matrix; the columns represent the unique instances of the features identified (i.e., specific sizes), the rows individual components, and the presence of a particular feature in a component is indicated by a one, otherwise zero. Figure 7 illustrates how the sequences shown in Table 2 are stored in a matrix form. All analyses methods use this matrix, known as the “Feature Content Matrix” as input, and each of the modeling approaches aims to capture the associations within and between feature type.
Fig. 7. Binary matrix representation of the feature content of the components detailed in Table 2. Feature presence in a component is indicated by a 1.
N-Gram
An N-Gram is a contiguous sequence of “n” items from a given sequence of features extracted from a component. Google created linguistics N-Grams by digitizing texts in the English language from between 1800 and 2000; 4% of “all books ever printed” (Michel et al., Reference Michel, Shen, Aiden, Veres, Gray, Pickett, Hoiberg, Clancy, Norvig and Orwant2011). These N-Grams are widely used in linguistics search and prediction. In principle, N-Grams can be generated from any sequence of text or numbers, however language grammar rules create an implicit ordering to many sequence of words, whereas the features extracted from the CAD model are have no canonical order which adds complexity to the prediction problem.
The frequency and co-occurrence of features present in the database can be used to estimate the required conditional probabilities for the feature prediction. The univariate probability of each feature being present in a design can be calculated using 
$\Pr ( f_x) = {\sum _1^N 1( f_x) }/{N}$, and equivalent to the calculation of bi-grams, the probabilities of subsequent features can be calculated using 
$\Pr ( f_{x + 1}\, \vert \, f_x) = {\sum ^N 1( f_{x + 1} \cap f_x) }/{\sum ^N 1( f_x) }$, where 
$f_x$ is the previously selected feature, and with constraint 
$\sum _p \Pr ( f_p \cap f_1) = 1$ (Brown et al., Reference Brown, Della Pietra, Desouza, Lai and Mercer1992). These probabilities can then be used to generate suggestions by ranking the bi-gram probabilities for each prospective feature in the descending order. This process can be generalized to N-Grams to include the previous 
$O$ holes in the probability calculation as further holes are sequentially added to the design. As an example using the data in Figure 7, the univariate probabilities of feature presence can be calculated by summing the columns and dividing by the number of rows (components), for example, 
$\Pr ( f_{h10}) = 4/5 = 0.8$ and the bi-gram conditional probabilities, which are used for ranking the next feature, by the sum of the set intersection divided by the univariate count, for example, 
$\Pr ( f_{h10}\, \vert \, f_{h14}) = $ 
$ \sum 1( f_{h10} \cap f_{h14}) /\sum 1( f_{h14}) = 3/4 = 0.75$.
Bayesian networks
Bayesian networks (BNs; Pearl, Reference Pearl1988; Cowell et al., Reference Cowell, Dawid, Lauritzen and Spiegelhalter2006) can be used to represent a set of variables and their conditional independencies via a directed acyclic graph. Formally, given a set of random variables 
$X$, a known graphical structure 
$G$, and the fully specified local probability distribution at each node (variable), the joint probability distribution of the network is defined as 
$\Pr ( X) = \prod _{i = 1}^N \Pr ( f_i\, \vert \, \pi _{f_i})$ where 
$\pi _{f_i}$ are the set of nodes from which there is a direct edge to node 
$f_i$, and 
$\Pr ( f_i\, \vert \, \pi _{f_i})$ defines the local probability distribution of node 
$f_i$ conditioned on the node set 
$\pi _{f_i}$. Features are directly associated if there is a edge or directed path between them (in the graph 
$f_1 \rightarrow f_2 \rightarrow f_3$, the nodes 
$f_1$ and 
$f_3$ are dependent), or nodes may become dependent conditional on the instantiation of other nodes in the graph (in the graph 
$f_1 \rightarrow f_2 \leftarrow f_3$, 
$f_1$ and 
$f_3$ are independent unless the value of 
$f_2$ is known). There are two tasks in learning a BN from the feature database, learning the structure of the graph, and learning the parameters, which together represent the associations between the features within the data as a product of conditional probabilities.
The graph structure was estimated from the binary matrix using a hill-climbing algorithm which iteratively adds, removes, or reverses an edge between the variables (i.e., features) based on some measure of statistical fit, and the result of the search is a directed graph that encodes the conditional independencies between the features. This measure of fit was computed by different methods; Akaike information criteria (AIC; Akaike, Reference Akaike, Parzen, Tanabe and Kitagawa1998), Bayesian information criteria (BIC; Schwarz et al., Reference Schwarz1978), or the Bayesian Dirichlet Sparse score (BDs; Scutari, Reference Scutari2016). The BN graph learned using the BDs resulted in a less sparse solution and was found to maximize the cross-validated recall@k when 
$k$ was 5 (defined in the section “Evaluation”), and the presented results which follow are for BNs learned using this score. Supplementary Material S2 shows the BN learned from the database.
Conditional probabilities were estimated using the Dirichlet posterior, setting the Dirichlet hyperparameter alpha to one (Scutari, Reference Scutari2016). Probability queries were then evaluated using Monte Carlo particle filters which draw samples from the probability tables across the graph. Suggestions were again generated by ranking the conditional probabilities of features given some observations. The statistical software package R v4.0 (R Core Team, 2020) and the R package bnlearn (Scutari, Reference Scutari2010) were used for this analysis.
Artificial neural networks
An Artificial Neural Network (ANN; Goodfellow et al., Reference Goodfellow, Bengio, Courville and Bengio2016) is based on a collection of connected units or nodes called artificial neurons. An artificial neuron that receives a signal, processes it and can then signal the neurons connected to it. In ANN implementations, the signal at a connection is a real number, and the output of each neuron is computed by some nonlinear function of the sum of its inputs. Autoencoder neural networks offer an unsupervised approach to learn the associations in data without labels. The data act as both the input and target variables, and in learning the aim is to recover the input from the compressed hidden layer. Through experimentation, it was found that a minimal architecture with one hidden layer and drop-out performed best. The NN architecture is shown in Figure 8. Predictive performance was sensitive to the number of hidden units and a greedy search in powers of two led to 1024 hidden units being used. The large number of hidden units and low compression was required to capture the information between the sparse features. The ANN was trained on minimizing the binary cross-entropy and the drop-out rate selected using a grid search allowing for early-stopping based on validation set loss (Srivastava et al., Reference Srivastava, Hinton, Krizhevsky, Sutskever and Salakhutdinov2014). The estimated ANN parameters were then used to predict the probability that a feature was present given some observations. The Python software package Keras (Chollet et al., Reference Chollet2015) using the tensorflow backend (Abadi et al., Reference Abadi, Agarwal, Barham, Brevdo, Chen, Citro, Corrado, Davis, Dean, Devin, Ghemawat, Goodfellow, Harp, Irving, Isard, Jia, Jozefowicz, Kaiser, Kudlur, Levenberg, Mané, Monga, Moore, Murray, Olah, Schuster, Shlens, Steiner, Sutskever, Talwar, Tucker, Vanhoucke, Vasudevan, Viégas, Vinyals, Warden, Wattenberg, Wicke, Yu and Zheng2015) were used for this analysis.
Fig. 8. Neural network autoencoder with dropout.
Evaluation
The predictive performance of each method was evaluated using 10-fold cross-validation which provides an approach to assess how well each model would predict subsequent features given a new design (Hastie et al., Reference Hastie, Tibshirani and Friedman2017). The learned models were used to estimate and rank the posterior probabilities of the features given observations from the test dataset; predictions were evaluated for one, two, or three observed features, and performance statistics generated for all combinations of the features present in a test component of cardinality equal to the number of observed features. For predictions to be validated, the test set retained components with at least one more feature than the number of observed features in the testing process. Using the sequences provided in Table 2 to illustrate; taking hole h14 as the one observed feature in the first component, predicted probabilities, 
$\Pr ( f_x\, \vert \, f_{h14})$, were calculated for all remaining features, 
${ f_x} -{ f_{h14}}$, in the training dataset. The highest-ranked predicted features were compared against the features present in the test set (e.g., where did the predictions for features 
$h10,\; h12,\; \ldots ,\; b110$ rank in the predictions calculated using the training dataset) and several information retrieval measures calculated to characterize any agreement; precision@k gives the proportion of predicted features within rank 
$k$ that were found in the test set (e.g., that were relevant) and recall@k gives the proportion of all relevant features that were found within rank 
$k$. These statistics are calculated in the presence of ties using the methods of McSherry and Najork (Reference McSherry and Najork2008). The retrieval statistics were averaged within each component, and then across all the components in the test set.
Assessment of predictive performance
A range of CAD industrial valve body designs were downloaded in STEP file format from an online parts library and the features extracted from these parts are made available at a DOI Archive. The scope of our investigation was restricted to through-holes and cylindrical bosses, because of their frequency in mechanical valves designs in the dataset, but the approach could be easily extended to other feature types (see Table 4).
The “Twig Match” algorithm was used to extract features from the CAD models using an efficient subgraph isomorphism identification procedure to enable the searching of thousands of components (represented in a B-rep face adjacency graphs) in less than a second (Paterson and Corney, Reference Paterson and Corney2016). This algorithm helps to flexibly search feature matches and accurately describe geometrical similarity rather than searching only for global similarity or rule-based feature match. Further details are provided in Vasantha et al. (Reference Vasantha, Purves, Quigley, Corney, Sherlock and Randika2021).
Data description
Our analysis database contains 513 valve bodies from which 344 distinct hole diameters and 701 cylindrical boss diameters were extracted. We recorded whether a specific diameter was in a design, and not how many times it occurs, and so the dataset can be represented by a 513 by 1045 binary matrix. The hole feature presence is sparse in terms of the how often a unique hole appears across the different designs and in terms of how many hole features a single design may have. While there are 34 (3%) of features that occur in greater than 5% of the designs most appear in fewer, and 337 (32%) of the feature diameters are only used in one design. On average, a design may have 11 distinct feature diameters (3.7 holes/7.3 bosses) with a minimum of 2 and maximum of 19, out of the set of 1045 features. This sparsity of information makes it a challenging prediction task.
Results
The predictive performance of each analysis method was evaluated using cross-validation. The N-Gram and BN methods outperform the ANN when there is only one feature in the current design. As additional features were included in the design, then both the BN and ANN provide the most relevant predictions.
Figures 9 and 10 provide the distribution of the prediction statistics across the ten-folds for when 
$k$ equals five and when there are either one, two, or three features already in the current design. Recall@k increased from around 30% to 50% and precision@k from around 50% to 70% as additional features were added. It is noted that the recall performance at 
$k = 5$ is dependent on the number of features present in a test design, which is on average 11. Therefore, the increases in precision and recall, as additional features were added to the design corresponds to, on average, between two and three out of the five feature suggestions being relevant up to four relevant suggestions. These results are the characteristic of CAD models with very similar designs, where the presence of a small number of features will lead to high predictability for subsequent ones. Suggestions generated by the N-Gram approach may be initially slightly more accurate, or relevant, when compared against those from the BN model, however the BN performs better as additional features were added to the design. The ANN struggles in each measure when only one feature is used to generate predictions, however, the addition of an additional features in the design leads to a large improvement in performance. One explanation for this could be that with additional features the test input gets closer to the input data from the ANN, and so improved reconstruction and performance.
Fig. 9. Distribution of recall@k across the ten cross-validation test folds for 
$k = 5$. The “observed” columns indicate the performance when either one, two, or three hole features were in the current design and predictions were made on a next relevant feature.
Fig. 10. Distribution of precision@k across the ten cross-validation test folds for 
$k = 5$. The “observed” columns indicate the performance when either one, two, or three hole features were in the current design and predictions were made on a next relevant feature.
Next, we examine how the performance depends on 
$k$; how many suggestions of relevant features are returned to the designer. Precision@k and recall@k were calculated for a range of 
$k$ from one to ten, which were then averaged across the ten-folds. Results are shown in Figure 11. As additional features were added to the current design, the predicted features were more likely to be relevant. The N-Gram method dominates predictions and are more relevant for all values of 
$k$ when there is only one feature in the new design, however as more features are added to the design the BN and ANN outperform the N-Gram method. The rate of increase in the recall slows at a faster rate using the N-Grams, predicting that a greater number of suggestions would have to be returned to capture all relevant features. This could be indicative of the issue of estimating probabilities on little data, but also could be due to variability found in our sample. A similar ranking in performance between the methods was observed when modeling the hole and boss features separately, and on a second smaller dataset on valve bonnets (results provided in the Supplementary Material S3 and S4).
Fig. 11. Precision and recall curves for each method – BN (solid), N-Gram (dashed), and ANN (dotted) – calculated at 
$K$ from 1 to 10. Recall increases as a greater number of suggestions are returned (as 
$k$ increases).
Discussion of results
It may have been expected that the N-Grams would outperform the BN, if the test datasets are representative of the data used to train the models, as it provides a lossless description of the pairwise frequencies (and probabilities) through the use of a greater number of parameters. However, as more features are added to a new design, then few components in the training data may have this combination of features and these low counts can lead to poor estimates of the probabilities. The BN approach to calculating these probabilities may offer improvements due to the factorized representation of these probabilities. The N-Grams method provides a way in which ranked predictions can be quickly generated using a simple lookup table, however, the method that we have used here requires that a different probability matrix is generated for every number of features that can be added to the new design. As an alternative, the probabilities calculated from lower order N-Grams could be used to make all predictions, for example, using the tri-gram probabilities to generate suggestions when there are more than two features in a new design, however in such a case, it would be expected that the predictive performance would be reduced.
The BN can be used to try to recover some underlying generative model which could be useful for understanding how certain features are associated, however, the best performing scores for structure learning were those which optimized the predictive performance and which led to less sparse associations. Additionally, due to the sparsity of the data, it is uncertain how robust these associations in the BN actually are. Generating predictions may require to be estimated by simulations and so may be more costly, in terms of time and space, than the other methods approaches.
The ANN performance was poor when a new design only contained one feature, which may be in part due to the small size of the data sample. The performance improved quickly with additional features and we would expect to see further improvement as more features are included in the new design. Furthermore, predictions can be generated from the previously learned model very quickly.
Prototype implementation and evaluation
The work presented is motivated by the belief that it provides the computational foundations for utilities that could be incorporated into the user interface of mechanical CAD systems. Consequently, operators of CAD systems and their assessment of its usefulness will be the ultimate judge of the work's success. There are many challenges in making such an assessment not least that because of the inherent subjectivity of human users who will inevitably be influenced by the own background and context. However, given the novelty of the proposed system even caveated feedback from users would help set the agenda for future research. So to assess the possible utility of a predictive CAD system, a plug-in based on the N-Gram approach has been developed and integrated with the SolidEdge™ CAD platform (Figure 12). The interface currently supports hole prediction and has an architecture that could be expanded to support slots, cut-outs, bosses, etc. Suggestions are generated by the design engineer selecting the plug-in from the toolbar and then choosing a point on one of the model's faces at which they want to create a hole. The selection of a face triggers a process that reads the diameter of all the existing holes on the CAD model. After the removal of any duplicate values, the list of unique hole diameters forms the input to the feature prediction algorithm and is used to determine which N-Gram algorithm is executed. For example, if the number of unique holes in the partial design is one, a bi-gram algorithm is executed. Similarly, if the number of unique holes is two, a tri-gram algorithm will be executed. After the appropriate N-Gram algorithm is executed, the predicted hole diameters are presented to the user has in a list of possibilities from which they choose to create a new hole feature at the location used to initiate the process.
Fig. 12. Screenshot of Prototype Predictive CAD (PCAD) Implementation in SolidEdge. Given the current hole features in the design, a set of ordered suggestions is provided to the engineer.
The potential of this prototype feature prediction CAD system was evaluated using a questionnaire survey. The questionnaire used a video of a CAD modeling session that used the prototype feature prediction application. This video narrates a situation where an engineer is working to create a valve body component. The participants completed the survey after watching the video. The web link to access the video used for evaluation is provided in Acknowledgment section. The parameters evaluated in the questionnaire were: the possibility of increasing feature re-use and decreasing modeling time, the potential for standardizing features, integrates well to the CAD modeling approach, and the likelihood and frequency of using the predictive system. In addition to these parameters, the participants also provided comments about the predictive system based on their personal experience. Twenty-seven experienced industrial mechanical engineers have completed the questionnaire. The average years of experience in engineering of the participants is 16 years (standard deviation 10 years). Table 3 summarizes the evaluation ratings marked by the experience engineers.
Table 3. Evaluation results of the predictive system
The evaluation results show that the engineers significantly agree that the proposed predictive system increases feature re-use, decreases CAD modeling time, standardizes features across CAD models, and integrates well to the CAD modeling approach. It is encouraging to observe that the engineers rated the likelihood of using the proposed predictive system highly. The frequency with which they might use the predictive system is rated moderate. The evaluation highlighted that CAD standardization will help build inventory for the company and would lead to a cost reduction of the product and so the product competitiveness, and enable design for manufacturing by allowing standard processes to be utilized on a range of products. The evaluation also observed that the benefit of the tool is that engineers do not have to look up for standard value and reduces the chance of clicking in bad information.
Figure 13 summarizes the improvement feedback provided by the experienced engineers in the proposed predictive system development approach. The evaluation noted that engineers expect more information in the predictive suggestions along with feature information such as cost, weight to enable judgemental decision. The semantic definition in the prediction problem could be expanded to include the additional parameters. Since the evaluation had been carried out with hole feature prediction, the expectation is to demonstrate for multiple other types of features. The presented research work in this paper further expands the predictive application to cylindrical boss features. The importance of creating open industrial feature databases is emphasized in the evaluation for better business integration. The evaluators emphasized the possible inclusion of confidence percentage along with the suggested features to enable correct decision and assure design quality. The evaluators suggested that the user interface could be improved by providing an option to show components that were associated with the suggested features as this would allow a quick visual check of the chosen feature's compatibility. Lastly, several evaluators suggested that it would be desirable if the predictive systems were integrated with existing product data management systems.
Fig. 13. Survey suggestions mapped onto the generic steps of the predictive CAD system implemented to support the assessment.
Although any survey of human users must consider issues of subjectivity and bias, the number and diversity of the participants (who, on average, had 16 years of CAD experience) will have moderated such effects. While the reported study provides some initial insights into the average CAD users assessment of the proposal to incorporate predictive functionality in a CAD interface, there is clearly scope for further investigations.
Extending the predictive models
The probability models can be extended by broadening the range of feature types used to potentially include all of those most commonly found in commercial CAD systems. There are two distinct types of feature extensions that can be considered. The first, which we refer to as expansions, can be done by increasing the range of symbols in the "Feature Content Matrix" that are used as input by the predictive models. Table 4 illustrates how the range of feature symbols could be extended from the holes and bosses used in the current study. Secondly, the association between features can be included; some examples include the co-direction of features or the distance between them. We refer to these additions as elaborations.
Table 4. Possible feature representations
However, although the extended syntax is easy to envisage, there are computational issues. Consider the situation of a set of hole diameter features with 
$n_h$ elements, which we combine with a set of boss features with 
$n_c$ elements. The first model, with hole features only, requires 
$n_h( n_h - 1)$ pairwise comparisons, and so the model with both sets have (n h + n c)(n h + n c − 1) =
$ n_h( n_h - 1) + n_c( 2n_h + n_c - 1)$ comparisons. Such additions will result in a quadratic growth in the number of evaluations between features that are required. This can result in large storage demands for the N-gram model, and as Bayesian network structure learning using search and score methods, for example, hill-climbing that was used in this analysis, is already exponential in the number of variables this can be expensive.
Furthermore, consider a feature that provides an elaboration on a relationship between elements, such as whether two elements are co-directional. For the set of holes, we would require an additional input vector of indicator variables of length 
$n_h + n_h( n_h - 1) /2$ resulting in 
$n_h( n_h - 1) /2 + n_h^2( n_h - 1) /2 =$ 
$ n_h( n_h - 1) ( n_h + 1) /2$ pairwise evaluations or potential direct links between features. Such a substantial increase in assessments can be prohibitive with regard to both limited data and so compromise the quality of inference or on calculations to support prediction real time.
For the Bayesian network modeling, we propose only considering assessing the likelihood of whether two features are co-directional on whether the features are present in the design or not. As such, we ignore any information provided by the presence or absence of any other features. The assumption is that the main driver is the relationship between the features and that the elaborations are modeled under this assumption, that a relationship between features is already there. This results in a quadratic number of comparisons only, that is, 
$n_h( n_h - 1) /2 + n_h( n_h - 1) =$ 
$ 3n_h( n_h - 1) /2$. Illustrating this with a simple example, consider a design that may have up to three different types of holes denoted by 
${\rm A},\; {\rm B}$, and 
${\rm C}$ and one type of elaboration, co-direction. We propose first learning the model to assess the association between the variables that indicate feature presence only, and then subsequently for each pair we have a child node assessing co-directionality, denoted by codir in Figure 14: the initial learned model is contained in the upper box and the elaboration in the lower box. So if feature 
${\rm A}$ was in the design and a prediction was required for an additional feature that was co-directional to 
${\rm A}$, then 
$\Pr ( {\rm B}\, \vert \, {\rm A},\; {\rm A}\ \text { and }\ {\rm B}\ \text { codir})$ and 
$\Pr ( {\rm C}\, \vert \, {\rm A},\; {\rm A} \ \text { and } \ {\rm C}\ \text { codir})$ could be evaluated by instantiating the co-direction indicator nodes separately.
Fig. 14. Extending the Bayesian network structure with elaborations to model further associations between features.
Similarly expansions for industrial standards which, say, specify bolt hole patterns on flanges (e.g., ISO5211, 2017) could be identified as entities at the feature extractions stage and then incorporated into predictive system by adding a symbol (e.g., ISO5211 F03) and analysis in the same way as other features. In another possible approach, the rules extracted from the standards could be established as de facto relationships between features in the data representation. The suggestions provided could present both feature relationships extracted from existing designs as well as from standards separately.
Discussion
The proposed feature-based sequence modeling system described here does not use the adjacency relationships (between components) that have previously been reported for component-based predictions. In contrast, the approach has been to identify the features which frequently “co-exist” on a component. This approach is motivated by the belief that predictions based on co-existing features will increase the likelihood that the suggested feature are appropriate to the current design state. In this way, the proposed feature-based prediction system will support partial design re-use to satisfy new requirements and provide an alternative to explicitly searching for similar designs to re-use. Instead, the predictive system implicitly generates a search query in the background of the design process and identifies specific feature suggestions for inclusion in an ongoing design activity. Another merit of the proposed system is that it does not require labeling of features and the preprocessing time to extract features from a database of components is not excessive.
The approach adopted for validating feature prediction compares the highest-ranked suggested features against the features present for each valve model in the test set. The application of 10-fold cross-validation has provided a robust evaluation for the three prediction approaches, and the prediction results are reasonable considering the size of the dataset and the sparsity of the feature co-existence in the used valve dataset. Each prediction method was able to extract patterns in the associations between the features to provide relevant predictions, and which could be further developed to provide useful decision support. The case-study provided some useful insights into the probability models relative strengths. The N-Grams provided good results compared to the other two approaches when there was only one feature in the design, however as more features were added the performance declined. This is due to being unable to estimate the conditional probabilities in these higher dimensions due to data sparsity. This is less of an issue for BN as these probabilities may be estimated through the product of several smaller probability estimates. The results suggest that at the initial stages of design where only one feature exists or where there is a large database of frequently co-occurring features, the N-Grams approach could produce the most useful suggestions. But subsequently, as a design develops, the Bayesian network or ANN approach could be better at generating relevant suggestions. Thus, the need to dynamically tailor the prediction approaches used for different stages of a design is the ultimate contribution of this research work.
The evaluation of the prototype system by experienced industrial engineers has highlighted some significant potential benefits that could be gained by enhancing product development and CAD modeling software with a predictive capability. In particularly, the possibility of increasing feature re-use, decreasing CAD modeling time, standardizing features across CAD models and integrating closely into the CAD modeling approach was noted. It is encouraging that many of the engineers observed that the predictive system are a natural evolution of existing CAD, and proposed a number of possible extensions for the proposed predictive system. Table 5 lists the proposed extensions to the predictive system and possible approaches to achieve it.
Table 5. Research agenda
The literature review resulted in the identification of eight distinguishing characteristics of predictive CAD system. These properties will enable the context of other prediction problems in industrial design to be described and ensure comparisons are appropriate.
The scope of the work reviewed was limited to systems that support designers to re-use existing components in the design process by active suggestion mechanisms. Therefore, the literature discussion did not include research articles related to automating design generation, such as generative design using the shape grammar approach (Zimmermann et al., Reference Zimmermann, Chen and Shea2018), computation design synthesis (Chakrabarti et al., Reference Chakrabarti, Shea, Stone, Cagan, Campbell, Hernandez and Wood2011), automatic adaptation techniques (Qin and Regli, Reference Qin and Regli2003), or parametric design exploration (e Costa et al., Reference e Costa, Jorge, Knochel and Duarte2020). Also, the presented research focuses only on the geometric CAD product data to enable re-use predictions during the design process and so did not discuss the literature associated with acquiring design rationale in the CAD design (Myers et al., Reference Myers, Zumel and Garcia2000), the prediction based on designer's behavior and preferences (Huang et al., Reference Huang, Su, Wu and Yang2020), case-based reasoning approach based on qualitative measures such as function-behavior-structure knowledge cell (Hu et al., Reference Hu, Ma, Feng and Peng2017) and query-based case retrieval system (Rivard and Fenves, Reference Rivard and Fenves2000). Also, the generation of rules from CAD datasets is not the focus of this research (Whiting et al., Reference Whiting, Cagan and LeDuc2018).
Conclusion and future work
This research has investigated how effectively N-Grams, NNs, and BNs are able to predict the occurrences of specific types of features that commonly occur in a family of valve body designs. The diameter of circular hole or cylindrical boss features were extracted from a dataset of valve body designs and were used as inputs for each predictive model. Results from the case-study indicate that the Bayesian network and neural network models generate more relevant predictions than those using N-Grams.
The predictive results suggest that the prototype system can already provide a useful level of support for valve designers. However, in other applications, such as text messaging and search, it is clear that the best predictive systems complement, rather than automate, a user's interactions with the system. The authors believe that the same approach should guide the development of predictive CAD systems. For example, the interaction between the designer and the predictive system could be increased by enabling the designer to explicitly reject (and not just ignore) some of the suggestions allowing the system to progressively improve its accuracy.
The user could also be given control of the nature and number of dataset used to generate suggestions. The current prototype, for example, uses different datasets for suggesting features when designing the body and bonnet components of the valves. So further work is required to investigate if it is possible to develop a prediction approach for combinations of different types of components.
There are also opportunities to improve the functionality of the underlying predictive models used by the prototype. For example, the scope of the current system could be extended to handle multiple types of features (such as holes, slots, pockets, and bosses) and also incorporate more parameter values than dimensions (such as feature occurrences and relative orientation).
The presented work focused on suggesting the next feature to be used, however the prediction systems could also be used to generate suggestions two or three steps ahead. In other words, the prediction algorithm could be used forecast multiple steps that will assist the designer in understanding the consequences of decisions made during the initial development stages.
Lastly, the results present reflect the behavior of the prediction algorithms when applied to one class of mechanical components (industrial valves). Further work will seek to establish how sensitive the results are to the particular sets of designs used.
Supplementary material
The supplementary material for this article can be found for this article can be found at https://doi.org/10.1017/S0890060422000014.
Acknowledgments
This work was supported by the Engineering and Physical Sciences Research Council, UK [grant number EP/R004226/1]. The dataset of hole features extracted from the valves models is available at https://bit.ly/38V9SX6. The video used for evaluating the predictive system can be accessed by this web link: https://youtu.be/ILK6QPI4v0o.
Gokula Vasantha is an Associate Professor in Engineering Design in the School of Engineering and the Built Environment at Edinburgh Napier University. Prior to joining the Napier University, he was working as a Research Associate/Fellow at the University of Strathclyde, Glasgow and Cranfield University, Bedford. He completed his PhD from the Indian Institute of Science (IISc), Bangalore, India in engineering design informatics. His interests include engineering design, engineering informatics, design methods, system modeling and analysis, crowdsourcing design and manufacturing, patent informatics, AI in engineering design, knowledge engineering, develop supportive engineering design tools, and product-service systems design.
David Purves is a researcher in the Department of Management Science at the University of Strathclyde. Research interests include probabilistic and multivariate modeling.
John Quigley is a Professor in the Department of Management Science and an Industrial Statistician with expertise in developing and applying statistical and stochastic methods to build decision support models. In particular, he has extensive experience of working with design engineers in developing models to inform reliable designs. He has been involved in such consultancy and research projects with, for example, Aero-Engine Controls, Rolls Royce, BAE SYSTEMS, IrvinGQ, and the MOD. His work in this area has become an industry standard for reliability growth analysis methods, BS/IEC 61164.
Jonathan Corney graduated with a degree in Mechanical Engineering from Heriot-Watt University in 1983 and then worked as a “junior robot designer” for the Westinghouse Electric Corp and a researcher at Edinburgh University's Department of Artificial Intelligence, before joining Heriot-Watt University as a lecturer, where he researched topics in mechanical CAD/CAM (e.g., feature recognition, 3D content-based retrieval). In 2007, he moved to the University of Strathclyde where he investigated manufacturing applications of crowdsourcing; cloud interfaces for manufacturing, the interactive search of digital media and, most recently, the creation of "predictive CAD systems" by leveraging data analytics. He was appointed Professor of Digital Manufacturing at the University of Edinburgh in January 2021.
Andrew Sherlock is a Director of Data-Driven Manufacturing at National Manufacturing Institute Scotland and a Professor of Practice at the University of Strathclyde. Until 2021, he was a Professor of Data-Driven Manufacturing at the University of Edinburgh. His first degree was in Mechanical Engineer and his PhD focused on novel shape optimization techniques for aerospace components. His subsequent career, both in academia and industry, has focused on the application of AI, data science and search techniques to design and manufacturing. In 2006, he founded ShapeSpace Ltd, a spin-out from the University of Edinburgh, to commercialize 3D search-by-shape technology, initially developed as a 3D search engine for components and subsequently enhanced to allow analysis of assemblies. This technology has been deployed at a number of large manufacturers in automotive, aerospace, and industrial equipment industries where the ability to do analytics on component portfolios and large numbers of bills of materials has uncovered significant cost savings within the supply chain. Between 2016 and 2019, he was the Royal Academy of Engineering (RAEng) Visiting Professor in Design for Product Profitability.
Geevin Randika is currently a final year student studying Mechanical Engineering at the University of Edinburgh. He was a research assistant at the University of Strathclyde Department of Design, Manufacture and Engineering Management assisting research in the field of Computer-Aided Design. His work involved in developing a predictive CAD platform to demonstrate predicting features in partial designs. Worked on CAD feature extraction techniques, cleaning and analysis of large CAD datasets.
Open access
