Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-25T01:47:49.533Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability Derivatives of Blunt Slender Cones at High Mach Numbers

Published online by Cambridge University Press:  07 June 2016

M. Khalid  and
R.A. East
M. Khalid
Affiliation:
Department of Aeronautics and Astronautics, University of Southampton
R.A. East
Affiliation:
Department of Aeronautics and Astronautics, University of Southampton
Get access

Summary

This paper presents a semi-empirical theoretical model for calculating the effect of nose bluntness on the stability derivatives of oscillating slender cones at hypersonic Mach numbers. It is based on a hybrid blast wave analogy/shock-expansion flow model and is used to obtain closed form analytic expressions for the derivatives 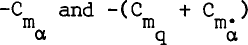for oscillating slender cones. Two models based on zero thickness and finite thickness entropy layers are proposed which are seen to be appropriate to the cases of very small and large nose bluntnesses, respectively. The results are compared with new and existing experimental data and with the predictions of previous theoretical methods.

Type
Research Article
Information
Aeronautical Quarterly , Volume 30 , Issue 4 , November 1979 , pp. 559 - 589
Copyright
Copyright © Royal Aeronautical Society. 1979

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1 East, R.A., Qasrawi, A.M.S. and Khalid, M. An experimental study of the hypersonic dynamic stability of pitching blunt conical and hyper-ballistic shapes in a short running time facility. AGARD CP 235, November 1978 Google Scholar
2 Ericsson, L.E. Effect of nose bluntness on the hypersonic unsteady aerodynamics of flared and conical bodies of revolution. AIAA Paper 68-889, August 1968 Google Scholar
3 Sieff, A. Secondary flow fields embedded in hypersonic shock layers. NASA TND-1304, May 1962 Google Scholar
4 Ericsson, L.E. Generalized unsteady embedded Newtonian flow. Journal of Spacecraft and Rockets, 12, p 718, December 1975 CrossRefGoogle Scholar
5 Rie, H., Linkiewicz, E.A. and Bosworth, F.D. Hypersonic dynamic stability, Part III, Unsteady flow field programme, FDL-TDR-64-149, Part III, January, 1967. Air Force Flight Dynamics Lab., Wright-Patterson Air Force Base Google Scholar
6 Orlik-Ruckemann, K.J. Dynamic viscous pressure interactions in hypersonic flow. National Research Council of Canada Aeronautical Rep. LR-535, July 1970 Google Scholar
7 Khalid, M. A theoretical and experimental study of the hypersonic dynamic stability of blunt axisymmetric conical and power-law shaped bodies. Ph.D. Thesis, University of Southampton, September 1977 Google Scholar
8 Chernyi, G.G. Introduction to hypersonic flow. Translation Editor Probstein, R.F., Academic Press, New York, 1961 Google Scholar
9 Eggers, A.J. and Savin, R.C. Approximate methods for calculating the flow about non-lifting bodies of revolution at high supersonic airspeeds. NACA, TN 2579, 1951 Google Scholar
10 Scott, C.J. A theoretical and experimental determination of the pitching stability derivatives of cones in hypersonic flow. M.Sc. Thesis (also AASU Report No. 267), University of Southampton, 1967 Google Scholar
11 Sims, J.L. Tables for supersonic flow around right circular cones at zero angle of attack1. NASA SP-3004, 1964 Google Scholar
12 Moore, R.K. and Ostrach, S. Displacement thickness of the unsteady boundary layer. Journal of Aero Sciences, 24 No. 1, pp 77–78, 1957 Google Scholar
13 Rainbird, W.J. Turbulent boundary layer growth and separation on a yawed cone. AIAA Journal, 6, No. 12, pp 2410–2416, December 1968 Google Scholar
14 Ericsson, L.E. Effect of nose bluntness, angle of attack and oscillation amplitude on hypersonic unsteady aerodynamics of slender cones. AIAA Journal, 9, pp 297–304, February 1971 Google Scholar
15 Krasnov, N.F. Aerodynamics of bodies of revolution, edited and annoted by Morris, Deane N.. American Elsevier Publication Company Inc., New York, 1970 Google Scholar
16 Curie, N. The steady compressible laminar boundary layer with arbitrary pressure gradient and uniform wall temperature. Proc. Roy. Soc. (A) 249, p 206, 1968 Google Scholar
17 Qasrawi, A.M.S. Measurements of hypersonic dynamic stability of pitching blunt-nosed bodies in a short duration facility. University of Southampton, Ph.D. Thesis, 1977 Google Scholar
18 Ericsson, L.E. Unsteady embedded Newtonian flow. Astronautica Acta, 18, pp 309–330, 1973 Google Scholar
19 Ericsson, L.E., Gunther, R.A., Stake, W.R. and Olmstead, G.W. Combined effects of nose bluntness and cone angle on unsteady aerodynamic Hypersonic turbulents. AIM Journal, 12, p 729, May 1974 Google Scholar
20 Ericsson, L.E. Effect of boundary layer transition on vehicle dynamics. Journal of Spacecraft and Rockets, 6, No. 12, pp 1404–1409, December 1969 Google Scholar
21 Mahood, G.E. and Hui, W.H. Remarks on unsteady Newtonian flow theory, Aeronautical Quarterly, 27, 66–74, 1976 Google Scholar