Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-05T21:30:20.898Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability and Response of Systems Satisfying a Second-Order Linear Differential Equation with Time-Dependent Coefficients

Published online by Cambridge University Press:  07 June 2016

A. W. Babister
A. W. Babister*
Affiliation:
The University, Glasgow
Get access

Summary

The differential equation considered is

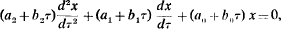
where all the a’s and b’s are real constants.

The nature of the solution is investigated in the neighbourhood of the singular point 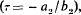and the conditions are found for logarithmic terms to be absent.

The conditions for stability for large values of τ are determined; the system is stable if

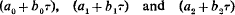
are all positive for large values of τ.

The form of the response is considered and its oscillatory (or non-oscillatory) nature investigated. The Sonin-Polya theorem is used to determine simple inequalities which must hold between the coefficients of the differential equation in any interval for the relative maxima of | x | to form an increasing or decreasing sequence in that interval.

Type
Research Article
Information
Aeronautical Quarterly , Volume 8 , Issue 1 , February 1957 , pp. 78 - 86
Copyright
Copyright © Royal Aeronautical Society. 1957

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Webb, H. A. and Airey, J. R. The Practical Importance of the Confluent Hypergeometric Function.PhiLMag. Series 6, Vol. 36, pp. 129, 1918.Google Scholar
2. Erdélyi, A., Magnus, W., Oberhettinger, F. and Tricomi, F. G. Higher Transcendental Functions.Vol. I. Bateman Manuscript Project. McGraw-Hill, 1953.Google Scholar
3. Ince, E. L. Ordinary Differential Equations. Longmans, 1926.Google Scholar
4. Whittaker, E. T. and Watson, G. N. Modern Analysis, Cambridge, 1935.Google Scholar
5. Erdélyi, A., Magnus, W., Oberhettinger, F. and Tricomi, F. G. Higher Transcendental Functions.Vol. II. Bateman Manuscript Project. McGraw-Hill, 1953.Google Scholar
6. Burnside, W. S. and Panton, A. W. Theory of Equations.Vol. I. Longmans, 1904.Google Scholar
7. Szegö, G. Orthogonal Polynomials. American Mathematical Society. Colloquium Publications. Vol. XXIII, 1939.Google Scholar