Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-22T11:52:58.553Z Has data issue: false hasContentIssue false
  • English
  • Français

Uncertainty analysis and robust shape optimisation for laminar flow aerofoils

Published online by Cambridge University Press:  03 August 2020

J. Hollom  and
N. Qin Open the ORCID record for N. Qin [Opens in a new window]
J. Hollom
Affiliation:
Department of Mechanical Engineering, The University of Sheffield, Sheffield, UK
N. Qin*
Affiliation:
Department of Mechanical Engineering, The University of Sheffield, Sheffield, UK
*
[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Uncertainty in the critical amplification factor (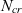 $N_{cr}$ ) of the $e^N$ transition model is used to approximate the uncertainty in the surface and flow quality of natural laminar flow (NLF) aerofoils. The uncertainty in 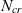$N_{cr}$ is represented by a negative half-normal probability distribution that descends from the largest 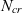$N_{cr}$ achievable with an ideal surface and flow quality. The uncertainty in various aerodynamic coefficients due to the uncertainty in 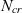$N_{cr}$ is quantified using the weighted mean and standard deviation of flow solutions run at different 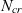$N_{cr}$ values. The uncertainty in the aerofoil performance is assessed using this methodology. It is found that the standard deviation of the aerofoil performance due to the uncertainty in 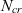$N_{cr}$ is largest when the transition location is most sensitive to changes in the lift coefficient at the ideal $N_{cr}$ . 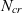Robust shape optimisation is also carried out to improve the mean performance and reduce the standard deviation of the performance with uncertainty in $N_{cr}$ . This is found to be effective at producing aerofoils with a larger amount of laminar flow that are less sensitivity to uncertainty in 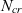$N_{cr}$ . A trade-off is observed between the mean performance and the standard deviation of the performance. It is also found that reducing the standard deviation of the performance at one Mach number or lift coefficient design point can cause an increase in the standard deviation off-design.

Keywords

Laminar transitionAmplification FactorUncertainty QuantificationRobust Optimisation
Type
Research Article
Information
The Aeronautical Journal , Volume 125 , Issue 1284 , February 2021 , pp. 365 - 388
Copyright
© The Author(s), 2020. Published by Cambridge University Press on behalf of Royal Aeronautical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Thomas, A.S.W. Aircraft drag reduction technology - a summary, in Aircraft Drag Prediction And Reduction, No. 723, Chapter 1, Advisory Group for Aerospace Research and Development (AGARD), July 1985.Google Scholar
Wagner, R. and Fischer, M. Developments in the NASA transport aircraft laminar flow program, 21st Aerospace Sciences Meeting, No. AIAA 83-0090, Reno, Navada, USA, January 1983. doi: 10.2514/6.1983-90.CrossRefGoogle Scholar
van Dam, C.P. and Holmes, B.J. Boundary-layer transition effects on airplane stability and control, J Aircr, 1988, 25, (8), pp 702–709. doi: 10.2514/3.45647.CrossRefGoogle Scholar
Braslow, A.L. and Fischer, M.C. Design considerations for application of laminar flow control systems, Aircraft Drag Prediction and Reduction, No. 723, Chapter 4, Advisory Group for Aerospace Research and Development (AGARD), July 1985.Google Scholar
Joslin, R.D. Aircraft laminar flow control, Annu Rev Fluid Mech, 1998, 30, (1), pp 1–29. doi: 10.1146/annurev.fluid.30.1.1.CrossRefGoogle Scholar
Young, T.M. and Humphreys, B. Liquid anti-contamination systems for hybrid laminar flow control aircraft – a review of the critical issues and important experimental results, J Aerosp Eng, 2004, 218, (4), pp 267–277. doi: 10.1243/0954410041872825.Google Scholar
Taguchi, G. and Wu, Y. Introduction to Off-Line Quality Control, Central Japan Quality Control Assoc., 1979.Google Scholar
Robitaille, M., Mosahebi, A. and Laurendeau, É. Design of adaptive transonic laminar airfoils using the $\gamma-\text{Re}_{\theta t}$ transition model, Aerosp Sci Technol, 2015, 46, pp 60–71. doi: 10.1016/j.ast.2015.06.027.Google Scholar
Rashad, R. and Zingg, D.W. Aerodynamic shape optimization for natural laminar flow using a discrete-adjoint approach, AIAA J, 2016, 54, (11), pp 3321–3337. doi: 10.2514/1.J054940.CrossRefGoogle Scholar
Huyse, L. and Lewis, R.M. Aerodynamic shape optimization of two-dimensional airfoils under uncertain conditions, ICASE Report 2001-1, NASA, Langley Research Center, Hampton, Virginia, USA, January 2001.Google Scholar
Li, W., Huyse, L. and Padula, S. Robust airfoil optimization to achieve consistent drag reduction over a Mach range, Contractor Report 211042, NASA, Langley Research Center, Hampton, Virginia, USA, August 2001.Google Scholar
Li, W. and Padula, S. Using high resolution design spaces for aerodynamic shape optimization under uncertainty, TP 2004-213003, NASA, Langley Research Center, Hampton, Virginia, USA, March 2004.Google Scholar
Lee, D.S., Gonzalez, L.F., Periaux, J. and Srinivas, K. Robust design optimisation using multi-objective evolutionary algorithms, Comput Fluids, 2008, 37, pp 565–583. doi: 10.1016/j.compfluid.2007.07.011.Google Scholar
Shimoyama, K., Oyama, A. and Fujii, K. Development of multi-objective six-sigma approach for robust design optimization, J Aerosp Comput Inf Commun, 2008, 5, (8), 215–233. doi: 10.2514/1.30310.CrossRefGoogle Scholar
Xiaopinga, Z., Jifengb, D., Weijia, L. and Yong, Z. Robust airfoil optimization with multi-objective estimation of distribution algorithm, Chin J Aeronaut, 2008, 21, pp 289–295. doi: 10.1016/S1000-9361(08)60038-2.Google Scholar
Croicu, A.-M., Hussaini, M.Y., Jameson, A. and Klopfer, G. Robust airfoil optimization using maximum expected value and expected maximum value approaches, AIAA J, 2012, 50, (9), pp 1905–1919. doi: 10.2514/1.J051467.CrossRefGoogle Scholar
Shah, H., Hosder, S., Koziel, S., Tesfahunegn, Y.A. and Leifsson, L. Multi-fidelity robust aerodynamic design optimization under mixed uncertainty, Aerosp Sci Technol, 2015, 45, pp 17–29. doi: 10.1016/j.ast.2015.04.011.CrossRefGoogle Scholar
Cook, L.W. and Jarrett, J.P. Robust airfoil optimization and the importance of appropriately representing uncertainty, AIAA J, 2017, 55, (11), pp 3925–3939. doi: 10.2514/1.J055459.CrossRefGoogle Scholar
Cook, L.W., Jarrett, J.P. and Willcox, K.E. Extending horsetail matching for optimization under probabilistic, interval, and mixed uncertainties, AIAA J, 2018, 56, (2), pp 849–861. doi: 10.2514/1.J056371.CrossRefGoogle Scholar
Zhao, L., Dawes, W.N., Parks, G., Jarrett, J.P. and Yang, S. Robust airfoil design with respect to boundary layer transition, 50th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, number AIAA 2009-2273, Palm Springs, California, USA, May 2009. doi: 10.2514/6.2009-2273.CrossRefGoogle Scholar
Zhao, K.,Gao, Z.-H. and Huang, J.-T. Robust design of natural laminar flow supercritical airfoil by multi-objective evolution method, Appl Math Mech, 2014, 35, pp 191–202. doi: 10.1007/s10483-014-1783-6.Google Scholar
Jing, L., Zhenghong, G., Jiangtao, H. and Ke, Z. Chin J Aeronaut, 2013, 26, (2), pp 309–318. doi: 10.1016/j.cja.2013.02.007.CrossRefGoogle Scholar
Salahudeen, A. and Baeder, J.D. Uncertainty quantification for free stream turbulence intensity effects on airfoil characteristics, AIAA Aerospace Sciences Meeting, No AIAA 2018-0033, Kissimmee, FL, USA, January 2018. doi: 10.2514/6.2018-0033.CrossRefGoogle Scholar
Deng, L. and Qiao, Z.D. A multi-point inverse design approach of natural laminar flow airfoils, 27th International Congress of the Aeronautical Sciences, Nice, France, September 2010.Google Scholar
Han, Z.-H., Chen, J., Zhu, Z. and Song, W.-P. Aerodynamic design of transonic natural-laminar-flow (nlf) wing via surrogate-based global optimization, 54th AIAA Aerospace Sciences Meeting, No. AIAA 2016-2041, San Diago, CA, USA, January 2016. doi: 10.2514/6.2016-2041.CrossRefGoogle Scholar
Drela, M. Xfoil: An analysis and design system for low Reynolds number airfoils, in Mueller, T.J. (Ed), Low Reynolds Number Aerodynamics, Notre Dame, Indiana, USA, Springer, June 1989, Berlin, Heidelberg, pp 1–12. doi: 10.1007/978-3-642-84010-4_1.Google Scholar
Drela, M. and Giles, M.B. Viscous–inviscid analysis of transonic and low Reynolds number airfoils, AIAA J, 1987, 25, (10), pp 1347–1355.CrossRefGoogle Scholar
Atkin, C.J. and Gowree, E.R. Recent developments to the viscous Garabedian and Korn method, 28th International Congress of the Aeronautical Sciences, Brisbane, Australia, September 2012.Google Scholar
Lock, R.C. and Williams, B.R. Viscous-inviscid interactions in external aerodynamics, Prog Aerosp Sci, 1987, 24, pp 51–171.CrossRefGoogle Scholar
Garabedian, P.R. and Korn, D.G. Analysis of transonic airfoils, Commun Pure Appl Math, 1971, 24, (6), pp 841–851.CrossRefGoogle Scholar
Lock, R.C. A review of methods for predicting viscous effects on aerofoils and wings at transonic speeds, in Computation of Viscous–Inviscid Interactions, No. 291, Chapter 2, Advisory Group for Aerospace Research and Development (AGARD), May 1981.Google Scholar
Green, J. E., Weeks, D.J. and Brooman, J.W.F. Prediction of turbulent boundary layers and wakes in compressible flow by a lag-entrainment method, Tech Rep 3791, Aeronautical Research Council, Aerodynamics Department, RAE Farnborough, UK, 1977.Google Scholar
Atkin, C.J. Convergence of calculated transition loci during computational analysis of transonic aerofoils and infinite swept wings, 29th Congress of the International Council of the Aeronautical Sciences, St. Petersburg, Russia, September 2014.Google Scholar
Gowree, E.R. Influence of Attachment Line Flow on Form Drag, PhD thesis, City University, London, UK, May 2014.Google Scholar
Somers, D.M. Design and experimental results for a flapped natural-laminar-flow airfoil for general aviation applications, TP 1865, NASA, Langley Research Center, Hampton, Virginia, USA, June 1981.Google Scholar
Wicke, K., Linke, F., Gollnick, V. and Kruse, M. Insect contamination impact on operational and economic effectiveness of natural-laminar-flow aircraft, J Aircr, 2016, 53, (1), pp 158–167. doi: 10.2514/1.C033237.CrossRefGoogle Scholar
Smith, A.M.O. and Gamberoni, N. Transition, Pressure Gradient and Stability Theory, Tech Rep 26388, Douglas Aircraft Company, El Seguno, CA, USA, August 1956.Google Scholar
Drela, M. Design and optimization method for multi-element airfoils, Aerospace Design Conference, No. AIAA 93-0969, Irvine, CA, USA, February 1993. doi: 10.2514/6.1993-969.Google Scholar
Driver, J. and Zingg, D.W. Numerical aerodynamic optimization incorporating laminar-turbulent transition prediction, AIAA J, 2007, 45, (8), pp 1810–1818. doi: 10.2514/1.23569.CrossRefGoogle Scholar
Cook, P.H., McDonald, M.A. and Firmin, M.C.P. Aerofoil RAE 2822 - pressure distributions, and boundary layer and wake measurements, Experimental Data Base for Computer Program Assessment, No. 138, Advisory Report A6, Advisory Group for Aerospace Research and Development (AGARD), May 1979.Google Scholar
Tamigniaux, T.L.B., Stark, S.E. and Brune, G.W. An experimental investigation of the insect shielding effectiveness of a Krueger flap/wing airfoil configuration, 5th Applied Aerodynamics Conference, No 87-2615, Monterey, CA, USA, August 1987, AIAA. doi: 10.2514/6.1987-2615.Google Scholar
Co, Boeing. High Reynolds number hybrid laminar flow control (HLFC) flight experiment II. Aerodynamic design, Tech Rep CR-1999-209324, NASA, Langley Research Center, Hampton, Virginia, USA, April 1999.Google Scholar
van Dam, C.P. The aerodynamic design of multi-element high-lift systems for transport airplanes, Prog Aerosp Sci, 2002, 38, (2), pp 101–144. doi: 10.1016/S0376-0421(02)00002-7.CrossRefGoogle Scholar
Schrauf, G. Large-scale laminar flow tests evaluated with linear stability theory, 19th Applied Aerodynamics Conference, AIAA, June 2001.CrossRefGoogle Scholar
Schmitt, V., Archambaud, J.P., Horstmann, K.H. and Quast, A. Hybrid laminar fin investigations, Active Control Technology for Enhanced Performance Operational Capabilities of Military Aircraft, Land Vehicles and Sea Vehicles, No RTO-MP-051, Braunschweig, Germany, June 2001. doi: 10.14339/RTO-MP-051.Google Scholar
Fortin, F.-A., Rainville, F-M.D.,Gardner, M.-A., Parizeau, M. and GagnÉ, C. Deap: Evolutionary algorithms made easy, J Mach Learn Res, 2012, 13, pp 2171–2175.Google Scholar
Deb, K., Pratap, A., Agarwal, S. and Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II, IEEE Trans Evol Comput, 2002, 6, (2), pp 182–197. doi: 10.1109/4235.996017.CrossRefGoogle Scholar
Deb, K. and Agrawal, R.B. Simulated binary crossover for continuous search space, Complex Syst, 1995, 9, (9), pp 115–148.Google Scholar
Deb, K. and Agrawal, S. A niched-penalty approach for constraint handling in genetic algorithms, Artificial Neural Nets and Genetic Algorithms, Slovenia, Indian Institute of Technology Kanpur, Springer, 1999, pp 235–243.CrossRefGoogle Scholar
Masters, D.A., Taylor, N.J., Rendall, T.C.S., Allen, C.B. and Poole, D.J. Review of aerofoil parameterisation methods for aerodynamic shape optimisation, 53rd AIAA Aerospace Sciences Meeting and Exhibit, No AIAA 10.2514/6.2015-0761, Kissimmee, FL, USA, January 2015. doi: 10.2514/6.2015-0761.CrossRefGoogle Scholar
Alander, J.T. On optimal population size of genetic algorithms, Computer Systems and Software Engineering 1992, The Hague, Netherlands, IEEE, May 1992, pp 65–70. doi: 10.1109/CMPEUR.1992.218485.Google Scholar
Storn, R. On the usage of differential evolution for function optimization, North American Fuzzy Information Processing, Berkeley, California, USA, IEEE, June 1996, pp 519–523.Google Scholar
Kulfan, B.M. Universal parametric geometry representation method, J Aircr, 2008, 45, (1), pp 142–158. doi: 10.2514/1.29958.Google Scholar