Published online by Cambridge University Press: 04 July 2016
One of the more important objectives of research in aerodynamics is drag reduction. In this paper we consider one part of the drag problem, the forebody pressure drag, and enquire about the lower limit to which it may theoretically be reduced by elimination of flow separation. It is customary to decompose the total drag force into two parts: pressure drag and friction drag, represented by force coefficients CD and CF, respectively. The ratio of these two forces may be taken as a convenient criterion to decide whether a body is ‘streamlined’ or ‘bluff’:
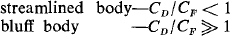
At high enough Reynolds numbers many bodies of interest are (according to this definition) bluff bodies, i.e. their pressure drag is much larger than the friction drag. This analysis is most relevant for bluff bodies where one needs to be concerned only with the pressure drag.