Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T01:24:25.138Z Has data issue: false hasContentIssue false
  • English
  • Français

The Rates of Change of the Eigenvalues of a Lambda Matrix and their Use in Flutter Investigations

Published online by Cambridge University Press:  04 July 2016

D. L. Woodcock
D. L. Woodcock*
Affiliation:
Structures Department, Royal Aircraft Establishment, Farnborough
Get access Rights & Permissions [Opens in a new window]

Extract

Consider a lambda matrix F(ƛ, δ). This may, for example, result from the equation of motion of a dynamical system, δ being a measure of the magnitude of some possible modification to the system or some other variable parameter. Let λ be an eigenvalue and p’ and q the corresponding left hand and right hand eigenvectors. Then

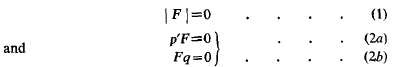
One wishes to determine the derivatives of ƛ with respect to δ. Expressions for the first two derivatives will be obtained on the assumptions that F is simply degenerate and that ƛ is not a repeated root.

Type
Technical Notes
Information
The Aeronautical Journal , Volume 70 , Issue 662 , February 1966 , pp. 364 - 365
Copyright
Copyright © Royal Aeronautical Society 1966

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Woodcock, D. L. The Cure of Flutter—A Quick Way of Investigating the Effect of Modifications. RAE Tech Note Structures 358, 1964.Google Scholar
2.Wittrick, W. H.Rates of Change of Eigenvalues with Reference to Buckling and Vibration Problems. Journal of the Royal Aeronautical Society, Vol. 66, September 1962.Google Scholar
3.Frazer, R. A., Duncan, W. J. and Collar, A. R.Elementary Matrices. Cambridge University Press 1938.CrossRefGoogle Scholar