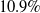Nomenclature
-
 $A{R_{{\rm{wb}}}} $
$A{R_{{\rm{wb}}}} $
-
CRM wingbox aspect ratio
-
 ${b_{{\rm{wb}}}} $
${b_{{\rm{wb}}}} $
-
CRM wingbox span
- DOF(s)
-
degree(s) of freedom
- FE
-
finite element
-
 $g $
$g $
-
constraint function
-
 $h $
$h $
-
CRM-like Box Beam height
-
 ${h_{{\rm{front}}}} $
${h_{{\rm{front}}}} $
-
CRM wingbox front spar height
-
 ${h_{{\rm{rear}}}} $
${h_{{\rm{rear}}}} $
-
CRM wingbox rear spar height
-
 ${h_s} $
${h_s} $
-
stiffener height
-
 $\boldsymbol{H}_{\Pi} $
$\boldsymbol{H}_{\Pi} $
-
hessian matrix of total potential energy
-
 $k $
$k $
-
spring stiffness
-
 $\boldsymbol{K}_{\rm{T}} $
$\boldsymbol{K}_{\rm{T}} $
-
tangent stiffness matrix
-
 $KS $
$KS $
-
Kreisselmeier–Steinhauser aggregated constraint function
-
 $l $
$l $
-
rod length; CRM-like Box Beam length
-
 $m $
$m $
-
mass
-
 $P $
$P $
-
applied load
-
 ${P_{\rm{c}}} $
${P_{\rm{c}}} $
-
critical buckling load of 1-DOF system
-
 ${P_{{\rm{design}}}} $
${P_{{\rm{design}}}} $
-
design load for optimisation
-
 ${P_{{\rm{end}}}} $
${P_{{\rm{end}}}} $
-
applied load at the end of the nonlinear analysis
-
 ${P_{{\rm{SOL}}105}} $
${P_{{\rm{SOL}}105}} $
-
linear buckling load predicted by SOL 105
-
 ${S_{{\rm{wb}}}} $
${S_{{\rm{wb}}}} $
-
CRM wingbox planform area
-
 $t $
$t $
-
wall thickness
-
 ${t_{{\rm{min}}}} $
,
${t_{{\rm{min}}}} $
,
 ${t_{{\rm{max}}}} $
${t_{{\rm{max}}}} $
-
thickness bounds for optimisation
-
 $ \boldsymbol{u} $
$ \boldsymbol{u} $
-
displacement vector
-
 ${u_{z,{\rm{\;}}n}} $
${u_{z,{\rm{\;}}n}} $
-
displacement along
 $z $
-axis evaluated at node
$z $
-axis evaluated at node
 $n $
$n $
-
 ${u_{z,{\rm{\;tip}}}} $
${u_{z,{\rm{\;tip}}}} $
-
displacement along
 $z $
-axis evaluated at the centre of the tip section
$z $
-axis evaluated at the centre of the tip section -
 $U $
$U $
-
internal strain energy
-
 ${V_{{\rm{wb}}}} $
${V_{{\rm{wb}}}} $
-
CRM wingbox volume
-
 $w $
$w $
-
CRM-like Box Beam width
-
 ${w_{{\rm{wb}}}} $
${w_{{\rm{wb}}}} $
-
CRM wingbox width
-
 $W $
$W $
-
external work done by conservative loads
Greek symbol
-
 ${\alpha _0} $
${\alpha _0} $
-
initial rod inclination
-
 $\beta $
$\beta $
-
twice rod rotation from initial configuration
-
 $\delta $
$\delta $
-
rod displacement
-
 ${\rm{\Delta }}s $
${\rm{\Delta }}s $
-
arc-length
-
 $\lambda $
$\lambda $
-
eigenvalue of tangent stiffness matrix
-
 $\mu $
$\mu $
-
scalar loading parameter
-
 ${\Pi} $
${\Pi} $
-
total potential energy
-
 $\rho $
$\rho $
-
Kreisselmeier–Steinhauser aggregation factor
-
 ${\sigma _k} $
${\sigma _k} $
-
von Mises stress of the
 $k $
-th element
$k $
-th element -
 ${\sigma _{{\rm{max}}}} $
${\sigma _{{\rm{max}}}} $
-
yield strength
-
 $\theta $
$\theta $
-
rod rotation angle of 1-DOF system
-
 ${\theta _0} $
${\theta _0} $
-
initial angle of asymmetry of 1-DOF system
-
 ${\theta _x} $
${\theta _x} $
-
average rotation of shell element about
 $x $
-axis
$x $
-axis
1.0 Introduction
In 2021, the Air Transport Action Group set the goal for global civil aviation operations to achieve net-zero carbon emission by 2050Footnote 1 . This goal is in line with the Paris Agreement, which aims to limit global warming to 1.5∘C and constitutes an ambitious challenge for the aviation sector.
Arising from these pressing environmental requirements, the objective of flying net-zero has further stimulated the everlasting quest for fuel-efficient aircraft designs. On a conceptual level, the well known Breguet Range equation indicates that fewer emissions will result from lighter aircraft, better aerodynamics and more efficient engines [Reference Filippone1]. In the last decades, the pursuit of lightweight structures has been supported by the development of aeroelastic optimisation tools, which usually search for minimum weight or minimum fuel burn configurations by navigating design spaces whose bounds are defined by structural and aeroelastic constraints. Having initially been developed for metallic structures, the advancement of these tools has been further stimulated by the advent of composite materials and the variety of design opportunities that they offer owing to their extensive elastic tailoring capabilities and their superior specific strength and stiffness properties in comparison to their metallic counterparts.
A critical aspect of aeroelastic optimisation is the consideration of static structural stability. This aspect has traditionally been enforced by means of linear buckling constraints, which are typically active for the optimised structure. The literature reveals several approaches to implementing these constraints.
The most straightforward approach involves global finite element analysis, where eigenvalue calculations are performed on a full wing model [Reference Sleesongsom and Bureerat2–Reference Keidel, Molinari and Ermanni7], returning buckling load multipliers (eigenvalues) and the corresponding buckling modes (eigenvectors). Elastic stability is understood to be lost at the load level corresponding to the applied load times the lowest multiplier. This method offers a balance between ease of implementation and the ability to capture overall structural stability, including interactions between different parts of the wing structure. However, it may not capture localised buckling phenomena as accurately as panel-level analyses and can be computationally expensive for highly detailed models.
To address these limitations, researchers have developed global-local eigenvalue calculation approaches, where separate global and local finite element models are considered [Reference Jrad, De and Kapania8–Reference Qian and Alonso10]. This technique combines the computational efficiency of panel-level analyses with the comprehensive structural representation of global models. It allows for a more nuanced treatment of buckling phenomena, capturing both localised panel instabilities and overall wing buckling modes, making it particularly useful for unconventional configurations like truss-braced wings or wings with curvilinear structural members.
For even more focused and computationally efficient analysis, some researchers employ eigenvalue calculations only on panel-level finite element models [Reference Stanford, Jutte and Wieseman11–Reference Kilimtzidis and Kostopoulos16]. This approach concentrates on individual skin panels, typically defined as areas bordered by adjacent ribs, spars and stringers. It allows for parallel computation of buckling modes across multiple panels, making it well-suited for large-scale optimisation problems involving numerous design variables and constraints.
To further reduce computational demands, panel-level Rayleigh-Ritz analysis has also been utilised [Reference Herencia, Weaver and Friswell17–Reference Stanford and Jutte19]. This method analyses individual wing panels using the principle of minimum potential energy, representing the out-of-plane displacement with assumed mode shapes, and formulating buckling once again as an eigenvalue problem. It offers an improved computational speed, avoiding the use of a finite element model, making it particularly suitable for preliminary design stages and optimisation studies involving variable stiffness panels.
Finally, the most computationally efficient approach is panel-level analytical analysis [Reference Kennedy and Martins20–Reference Gray and Martins25]. This method employs closed-form analytical or semi-empirical formulas to calculate critical buckling loads for individual wing panels. It often utilises a smeared-stiffener model, where the effects of discrete stiffeners are averaged over the panel area. This simplified approach is well-suited for large-scale aerostructural optimisation problems where the largest part of the computational budget is employed to increase the fidelity of other disciplines such as the calculation of the aerodynamic loads via RANS.
While these approaches offer varying levels of computational efficiency and detail, they all rely on the linearisation of the structural response around the undeformed configuration and consequently on the assumption that the response to loading is perfectly linear before the loss of stability. The use of these methods in low-fidelity preliminary aircraft design has thus far been considered to be conservative, because stiffener-reinforced panels buckle super-critically. In other words, their post-buckling is stable and the structure retains load-carrying capacity beyond the predicted stability limit. However, simplicity and conservativeness come at the cost of over-constraining the design space and consequently over-designing the structure because, in practice, it could carry more load. In fact, in the more advanced design stages, aerospace structures are indeed sized to carry loads beyond their linear buckling point [Reference Niu26].
In this paper, we hypothesise that, in current aeroelastic optimisations targeting aircraft structures, linear buckling analyses place an artificial limit on the load that the structure is sized for, which we refer as the glass ceiling of linear buckling. The resulting constraints prevent optimisers from exploring the part of the design space beyond this threshold, ultimately leading to designs that are heavier than necessary. In addition, the current trend towards more sustainable designs seeing the development of more slender, higher aspect ratio, and lighter wing structures, where nonlinear effects are more prominent, calls into question the validity of the assumed linearity pre-buckling.
At the same time, the incorporation of postbuckling effects in aeroelastic optimisation frameworks remains an open challenge. Although numerous studies have explored the optimisation of stiffened panels considering postbuckling constraints, very few have extended this approach to wingbox structures. The limited research on wingbox-level postbuckling optimisation has focused primarily on simplified models or specific components, lacking integration with comprehensive aeroelastic analysis. For instance, Qu et al. [Reference Qu, Kennedy and Featherston27] developed a multilevel optimisation framework for a composite aircraft wing, achieving significant mass reduction but using simplified loading conditions. Liguori et al. [Reference Liguori, Zucco, Madeo, Magisano, Leonetti, Garcea and Weaver28] focused only on a representative wingbox section using variable angle tow (VAT) composites, demonstrating improvements in buckling and postbuckling performance. Liang and Yin [Reference Liang and Yin29] introduced nonlinear buckling analysis for a Blended Wing Body configuration, but only as a post-optimisation step. To date, no aeroelastic optimisation framework has been developed that fully incorporates postbuckling constraints at the wingbox level while considering the complex interactions between aerodynamics, structural behaviour, and overall aircraft performance. Addressing this gap could unlock significant potential for weight reduction and improved structural efficiency in aircraft design.
To transcend this limitation and break through the glass ceiling of linear buckling, this work proposes a paradigm shift in approaching structural stability within aeroelastic optimisation. Instead of framing the problem in terms of buckling and postbuckling – a binary concept predicated on a predicted instability point – this work advocates for a more nuanced approach based on the continuous monitoring of structural equilibrium stability through the positive-definiteness of the tangent stiffness matrix. A novel nonlinear structural stability constraint is formulated based on this approach and it is tested in a simple structural optimisation problem: a stringer-reinforced box beam abstracted from NASA’s Common Research Model [Reference Vassberg, Dehaan, Rivers and Wahls30] (CRM).
The remainder of the paper is organised as follows. In Section 2, a brief overview of the theory behind nonlinear structural stability is given by means of three different canonical examples. Successively, a more complex problem is tackled in Section 3, where a straight box beam abstraction of the CRM wingbox is presented and its nonlinear response under a bending load is studied. Finally, the box beam is optimised in Section 4, employing the proposed nonlinear structural stability constraint, and the optimisation results are discussed with a focus on the effect of such constraint.
The results presented in this paper are reproducible by means of a jupyter notebook available in an open-source Github repositoryFootnote 2 , where more resources about the ongoing research efforts on the topic can also be found.
2.0 Nonlinear structural stability of canonical examples
This section illustrates the fundamental concepts of the continuous monitoring of structural stability, which underlies the proposed optimisation constraint. Three 1-DOF (degree of freedom) systems are considered to show the difference with the traditional approach by explaining three canonical behaviours that can be encountered in the nonlinear analysis of structures: the supercritical pitchfork bifurcation, the broken supercritical pitchfork and the limit point bifurcation. It should be noted that we consider the systems purely from a structural stability perspective and we intentionally neglect any considerations of strength. Here, we report the results for each system, while the full mathematical derivations are given in the Appendix.
2.1 Supercritical pitchfork bifurcation
For the first canonical example, we consider the perfectly symmetric 1-DOF system shown in Fig. 1, made of two initially collinear rods connected with a rotational spring and subjected to a compressive load.

Figure 1. Undeformed and deformed state of two initially collinear rods under axial compressive load.
To obtain the full nonlinear response of this system in terms of the applied load,
![]() $P $
, and the only degree of freedom,
$P $
, and the only degree of freedom,
![]() $\theta $
, we need to look at the total potential energy,
$\theta $
, we need to look at the total potential energy,
![]() ${\Pi} $
, which is given by the difference between the internal strain energy,
${\Pi} $
, which is given by the difference between the internal strain energy,
![]() $U $
, and the external work,
$U $
, and the external work,
![]() $W $
, done by conservative loads [Reference Bazănt and Cedolin31], such that
$W $
, done by conservative loads [Reference Bazănt and Cedolin31], such that
The equilibria of the system correspond to the points where the potential energy has a stationary value, or in other words where its first derivative with respect to the degree of freedom is zero, in the form of
The stability of each equilibrium point depends on the second derivative of the potential energy, thus
 \begin{align} \frac{{{\partial ^2}{\Pi}}}{{\partial {\theta ^2}}}{\rm{\;\;\;\;}}\left\{ {\begin{array}{l} { \gt 0\;\;\;\;{\rm{stable\;equilibrium}}}\\[3pt] { = 0{\rm{\;\;\;\;neutral\;equilibrium}}}\\[3pt] { \lt 0\;\;\;\;{\rm{unstable\;equilibrium}}.}\end{array}} \right. \end{align}
\begin{align} \frac{{{\partial ^2}{\Pi}}}{{\partial {\theta ^2}}}{\rm{\;\;\;\;}}\left\{ {\begin{array}{l} { \gt 0\;\;\;\;{\rm{stable\;equilibrium}}}\\[3pt] { = 0{\rm{\;\;\;\;neutral\;equilibrium}}}\\[3pt] { \lt 0\;\;\;\;{\rm{unstable\;equilibrium}}.}\end{array}} \right. \end{align}
The equilibrium equations of the system, as derived in the Appendix, are
 \begin{align}\left\{ {\begin{array}{l}{\theta = 0}\\[3pt] {P = {P_{\rm{c}}}\frac{\theta }{{{\rm{sin}}\,\theta }}}\end{array}} \right. \end{align}
\begin{align}\left\{ {\begin{array}{l}{\theta = 0}\\[3pt] {P = {P_{\rm{c}}}\frac{\theta }{{{\rm{sin}}\,\theta }}}\end{array}} \right. \end{align}
where
![]() $ {P_{\rm{c}}} = 2k/l $
is the critical buckling load. For
$ {P_{\rm{c}}} = 2k/l $
is the critical buckling load. For
![]() $\theta = 0 $
, the equilibrium is stable for
$\theta = 0 $
, the equilibrium is stable for
![]() $P \lt {P_{\rm{c}}} $
and unstable for
$P \lt {P_{\rm{c}}} $
and unstable for
![]() $P \gt {P_{\rm{c}}} $
, while for
$P \gt {P_{\rm{c}}} $
, while for
![]() $P = {P_{\rm{c}}}\theta /{\rm{sin}}\,\theta $
the equilibrium is always stable.
$P = {P_{\rm{c}}}\theta /{\rm{sin}}\,\theta $
the equilibrium is always stable.
The results are plotted in the load-displacement diagram shown in Fig. 2, depicting a supercritical pitchfork bifurcation. The supercritical pitchfork bifurcation is characterised by four equilibrium paths: a stable zero-displacement path for
![]() $P \lt {P_{\rm{c}}} $
, an unstable zero-displacement path for
$P \lt {P_{\rm{c}}} $
, an unstable zero-displacement path for
![]() $P \gt {P_{\rm{c}}} $
and two stable nonzero-displacement paths for
$P \gt {P_{\rm{c}}} $
and two stable nonzero-displacement paths for
![]() $P \gt {P_{\rm{c}}} $
. The point where these four equilibrium paths meet is called bifurcation point and is characterised by a neutral equilibrium.
$P \gt {P_{\rm{c}}} $
. The point where these four equilibrium paths meet is called bifurcation point and is characterised by a neutral equilibrium.

Figure 2. Supercritical pitchfork bifurcation of the two initially collinear rods.
The supercritical pitchfork bifurcation is the classic response where it is possible to identify a discrete critical point dividing the response itself into a pre-buckling and a post-buckling region. The linear buckling analysis correctly predicts the presence of a critical point at
![]() $P = {P_{\rm{c}}} $
, corroborating this division of the response.
$P = {P_{\rm{c}}} $
, corroborating this division of the response.
However, the linear analysis cannot predict the two nonzero-displacement stable paths for
![]() $P \gt {P_{\rm{c}}} $
. Consequently, in the linear approach, the predicted buckling load is taken as the limit load for the structure. This means that the linear approach places a glass ceiling on the sizing load of the structure, whereas, in reality, stable configurations are achievable beyond this threshold. However, these configurations remain unexplored without the insights provided by nonlinear analysis.
$P \gt {P_{\rm{c}}} $
. Consequently, in the linear approach, the predicted buckling load is taken as the limit load for the structure. This means that the linear approach places a glass ceiling on the sizing load of the structure, whereas, in reality, stable configurations are achievable beyond this threshold. However, these configurations remain unexplored without the insights provided by nonlinear analysis.
2.2 Broken supercritical pitchfork
The second canonical example is obtained by introducing an asymmetry into the previous 1-DOF system, given by an initial angle,
![]() ${\theta _0} $
, as shown in Fig. 3. The idea behind this second example is that, in reality, perfectly symmetric structural systems do not exist in aircraft, either because of their intrinsic geometry or for the applied load.
${\theta _0} $
, as shown in Fig. 3. The idea behind this second example is that, in reality, perfectly symmetric structural systems do not exist in aircraft, either because of their intrinsic geometry or for the applied load.

Figure 3. Undeformed and deformed state of two rods at an initial angle
![]() ${\theta _0} $
under axial compressive load.
${\theta _0} $
under axial compressive load.
Following the derivations in the Appendix, the equilibrium equation for the system is
and the equilibrium is stable for
![]() $\left( {\theta - {\theta _0}} \right)/{\rm{tan}}\,\theta \lt 1 $
and unstable for
$\left( {\theta - {\theta _0}} \right)/{\rm{tan}}\,\theta \lt 1 $
and unstable for
![]() $\left( {\theta - {\theta _0}} \right)/{\rm{tan}}\,\theta \gt 1 $
.
$\left( {\theta - {\theta _0}} \right)/{\rm{tan}}\,\theta \gt 1 $
.
The equilibrium paths of the system are plotted in Fig. 4 for different values of
![]() ${\theta _0} $
. In the figure it is possible to observe a broken supercritical pitchfork, where the load-displacement diagram of the structure is made of two disconnected paths. One path is connected to the ground state and is completely stable; we refer to this as the natural path. The other path cannot be reached from the ground state and is partly stable and partly unstable; we refer to it as the complementary path. It can also be observed that the two paths are further separated as the initial angle increases.
${\theta _0} $
. In the figure it is possible to observe a broken supercritical pitchfork, where the load-displacement diagram of the structure is made of two disconnected paths. One path is connected to the ground state and is completely stable; we refer to this as the natural path. The other path cannot be reached from the ground state and is partly stable and partly unstable; we refer to it as the complementary path. It can also be observed that the two paths are further separated as the initial angle increases.

Figure 4. Broken supercritical pitchfork of the two rods at an initial angle
![]() ${\theta _0} $
.
${\theta _0} $
.
It is important to notice that the introduction of the asymmetry into the system is responsible for the emergence of the broken supercritical pitchfork. A supercritical pitchfork bifurcation is only possible with a perfectly symmetric system; in such a system, the symmetry leads to the existence of at least one bifurcation point on the load-displacement diagram, where the equilibrium is neutral. When the symmetry of the problem is broken, the system maintains stability as it is loaded from its ground state and no critical point is encountered. Consequently, it is no longer possible to discretely identify a pre- and post-buckling response.
2.3 Limit point bifurcation
The third canonical example is given by the 1-DOF system shown in Fig. 5, comprising two inclined rods tied by an elastic support while subjected to transverse loading.

Figure 5. Undeformed and deformed state of two inclined rods with elastic support under transverse load.
The equilibrium equation of the system is given by
and the equilibrium is stable when
![]() $\left( {{\rm{cos}}\,{\alpha _0} - {\rm{co}}{{\rm{s}}^3}\,\theta } \right)/{\rm{cos}}\,\theta \gt 0 $
, and unstable or neutrally stable otherwise.
$\left( {{\rm{cos}}\,{\alpha _0} - {\rm{co}}{{\rm{s}}^3}\,\theta } \right)/{\rm{cos}}\,\theta \gt 0 $
, and unstable or neutrally stable otherwise.
The load-displacement diagram of the system is plotted in Fig. 6, in terms of nondimensional applied load
![]() $P/kl $
against the angle travelled by the inclined rods,
$P/kl $
against the angle travelled by the inclined rods,
![]() ${\alpha _0} - \theta $
, for an initial inclination of
${\alpha _0} - \theta $
, for an initial inclination of
![]() ${\alpha _0} = 30 $
degrees. Proceeding left to right, the diagram shows: a stable path originating from the ground state of the structure; a load limit point with neutral equilibrium in correspondence of the local maximum of the applied load; an unstable path where the applied load decreases with the angle travelled by the rods; another load limit point with neutral equilibrium at the local minimum of the applied load; and, finally, another stable path where the applied load increases again.
${\alpha _0} = 30 $
degrees. Proceeding left to right, the diagram shows: a stable path originating from the ground state of the structure; a load limit point with neutral equilibrium in correspondence of the local maximum of the applied load; an unstable path where the applied load decreases with the angle travelled by the rods; another load limit point with neutral equilibrium at the local minimum of the applied load; and, finally, another stable path where the applied load increases again.

Figure 6. Limit point bifurcation of the two inclined rods under transverse load.
This type of response is called limit point bifurcation and it results in a snapping behaviour. When the system is loaded from its ground state and the applied load exceeds the first load limit point, the structure snaps across the equilibrium manifold, traversing the region of instability, to land onto the first stable equilibrium point corresponding to the applied load. In practice, this means that the initially upwards inclined rods suddenly snap to assume a downwards inclination. This behaviour occurs because the structure needs to ‘jump’ to the other stable equilibrium path to find an equilibrium point with an applied load larger than that corresponding to the first limit point.
As a consequence of the above discussion, the first load limit point represents a discrete critical point that could be used to divide the response into a pre- and a post-snap region. However, contrary to the case of the supercritical pitchfork bifurcation, the presence of a snapping behaviour implies a discontinuity in the real structural response, meaning that the transition to the post-snap state does not happen in a quasi-static manner. It should also be noted that an accurate determination of the limit points can only be obtained with a continuous monitoring of the stability of the nonlinear equilibrium.
In the context of Finite Element (FE) analysis, the nonlinear equilibrium equations are often solved under load control. This is also the case in aeroelastic optimisation frameworks featuring nonlinear structural analysis [Reference Gray and Martins25, Reference Rajpal, Gillebaart and De Breuker32]. With this approach, a load value is imposed at every consecutive increment of the nonlinear analysis and held constant during Newton-Raphson iterations until convergence is achieved. Upon convergence, the analysis moves on to the next load increment. However, this method has issues with limit point bifurcations, because it cannot follow the unstable segment of the equilibrium path beyond the limit point, where the equilibrium load decreases. In fact, the solver might jump to the next available equilibrium point for the new increment above the limit point, or it might not achieve convergence at all [Reference Leon, Paulino, Pereira, Menezes and Lages33], as illustrated in Fig. 7. In both cases load controlled increments cannot find unstable equilibrium points, making it unsuitable for an aeroelastic optimisation framework that aims to evaluate structural stability with nonlinear methods. Displacement control would have no issues tracing curves with load limit points, but would equally be unable to converge past displacement limit points.

Figure 7. Non-convergence of the load control method across a limit point bifurcation.
A popular alternative to load (or displacement) control is path-following with arc-length control, which considers simultaneous variations of load and displacement variables. The basis of this method consists in constraining the solution path to an arc-length
![]() ${\rm{\Delta }}{s^i} $
, that is calculated via a norm of the increment
${\rm{\Delta }}{s^i} $
, that is calculated via a norm of the increment
![]() $\left( {{\rm{\Delta }}{ \textbf{u}^i},{\rm{\Delta }}{\mu ^i}} \right) $
, where
$\left( {{\rm{\Delta }}{ \textbf{u}^i},{\rm{\Delta }}{\mu ^i}} \right) $
, where
![]() $ \textbf{u} $
is the displacement vector,
$ \textbf{u} $
is the displacement vector,
![]() $\mu $
a scalar loading parameter, and
$\mu $
a scalar loading parameter, and
![]() $i $
is the increment number. The iterations are constrained to lie on the surface created by the arc, and they eventually converge at the intersection of the arc and the equilibrium path. In this way, arc-length methods can successfully calculate the equilibrium path of a structure also in presence of instabilities like limit point bifurcations [Reference Leon, Paulino, Pereira, Menezes and Lages33], as illustrated in Fig. 8. Consequently, the arc-length method is chosen for the application of the nonlinear structural stability constraint proposed in this paper, since it can successfully follow unstable segments of an equilibrium path.
$i $
is the increment number. The iterations are constrained to lie on the surface created by the arc, and they eventually converge at the intersection of the arc and the equilibrium path. In this way, arc-length methods can successfully calculate the equilibrium path of a structure also in presence of instabilities like limit point bifurcations [Reference Leon, Paulino, Pereira, Menezes and Lages33], as illustrated in Fig. 8. Consequently, the arc-length method is chosen for the application of the nonlinear structural stability constraint proposed in this paper, since it can successfully follow unstable segments of an equilibrium path.

Figure 8. Convergence of the arc-length control method across a limit point bifurcation.
3.0 Nonlinear structural stability of the CRM-like Box Beam
In this section, we evaluate the nonlinear structural stability of a reinforced box beam abstracted from the CRM wingbox, that is referred to as the CRM-like Box Beam. This model is developed to obtain a simplified wingbox structure that is still representative of the models employed in aeroelastic optimisations, and that retains the essential features that influence the nonlinear structural stability behaviour.
To obtain a simple geometry, the CRM-like Box Beam is defined as a straight, untapered wingbox with dimensions obtained as a geometric average of those of the CRM wingbox, based on the data provided by Taylor and Hunsaker [Reference Taylor and Hunsaker34]. The geometry and dimensions of the model are shown in Fig. 9. As it can be observed from the figure, the CRM-like Box Beam is internally reinforced by 19 equally spaced ribs and by 2 equally spaced stiffeners for each skin. Table 1 summarises the cross-sectional and material properties used for the numerical model. The initial structure has a constant wall thickness for all structural parts equal to 1/100th of the wingbox height. For the full derivation of the CRM-like Box Beam, the reader is referred to the Appendix.
Table 1. CRM-like Box Beam cross-sectional and material properties. Material properties from Ref. Reference Brooks, Kenway and Martins35)


Figure 9. Geometry and dimensions of the CRM-like Box Beam model.
To study the nonlinear structural stability of the CRM-like Box Beam under a bending deformation, fixed boundary conditions are enforced at the root section and a concentrated load,
![]() $P $
, is applied at the centre of the tip section along the
$P $
, is applied at the centre of the tip section along the
![]() $z $
-axis. The numerical model is implemented in MSC Nastran, where all geometrical parts are discretised into CQUAD4 elements. These are four-node quadrilateral shell elements with six degrees of freedom per node, employing the Mindlin-Reissner theory for their formulation. Clamped boundary conditions are defined for all the nodes at the root (
$z $
-axis. The numerical model is implemented in MSC Nastran, where all geometrical parts are discretised into CQUAD4 elements. These are four-node quadrilateral shell elements with six degrees of freedom per node, employing the Mindlin-Reissner theory for their formulation. Clamped boundary conditions are defined for all the nodes at the root (
![]() $y = 0 $
), and they are implemented by means of a SPC1 Nastran card. The load is introduced at a fictitious node at the centre of the tip section, which is connected to the nodes at the edge of the tip rib by means of an RBE3 Nastran card. This card defines a multipoint constraint that specifies the motion at the reference grid point as the weighted average of the motions at the set of connected grid points.
$y = 0 $
), and they are implemented by means of a SPC1 Nastran card. The load is introduced at a fictitious node at the centre of the tip section, which is connected to the nodes at the edge of the tip rib by means of an RBE3 Nastran card. This card defines a multipoint constraint that specifies the motion at the reference grid point as the weighted average of the motions at the set of connected grid points.
A mesh convergence study is performed by running MSC Nastran linear buckling solution sequence, SOL 105, with a concentrated unit load
![]() $P = 1{\rm{N}} $
for increasing mesh resolution and by monitoring the predicted linear buckling load,
$P = 1{\rm{N}} $
for increasing mesh resolution and by monitoring the predicted linear buckling load,
![]() ${P_{{\rm{SOL}}105}} $
. The results are summarised in Table 2. The mesh is considered to be converged when the difference of the linear buckling load with respect to that obtained with the finest mesh is below 1%.
${P_{{\rm{SOL}}105}} $
. The results are summarised in Table 2. The mesh is considered to be converged when the difference of the linear buckling load with respect to that obtained with the finest mesh is below 1%.
Table 2. Results of the mesh convergence study in terms of number of degrees of freedom, linear buckling loads and percentage differences with respect to the load obtained with the finest mesh

Figure 10 shows the critical buckling mode for the converged mesh, corresponding to a linear buckling load
![]() ${P_{{\rm{SOL}}105}} \approx 12,517{\rm{N}} $
. The critical buckling mode involves mainly the rib-stiffener panels closest to the root of the structure, indicating that, as expected, these panels experience the highest compressive stress. The figure also shows the location of node 455, that is the node undergoing the largest displacement in the critical buckling mode. We will use the displacement along the
${P_{{\rm{SOL}}105}} \approx 12,517{\rm{N}} $
. The critical buckling mode involves mainly the rib-stiffener panels closest to the root of the structure, indicating that, as expected, these panels experience the highest compressive stress. The figure also shows the location of node 455, that is the node undergoing the largest displacement in the critical buckling mode. We will use the displacement along the
![]() $z $
-axis at this node in the load-displacement diagrams obtained from the nonlinear analyses, and we will refer to it as the root displacement.
$z $
-axis at this node in the load-displacement diagrams obtained from the nonlinear analyses, and we will refer to it as the root displacement.

Figure 10. Critical buckling mode of the CRM-like Box Beam predicted by SOL 105.
As in Section 2, also in a nonlinear FE context, structural stability can be evaluated by considering the second derivative of the total potential energy, i.e. the Hessian of the system, which represents the tangent stiffness matrix of the structure. The stability of an equilibrium point is thus established as
 \begin{align}\frac{{{\partial ^2}{\Pi}}}{{\partial {{\bf{u}}^2}}} = { \boldsymbol{H}_{\Pi}}\left( \boldsymbol{u} \right) = {\boldsymbol{K}_T}\left( \boldsymbol{u} \right)\left\{ \begin{array}{rl}{{\rm{\;positive\;definite}}} & {} \Rightarrow {\rm{stable\;equilibrium}}\\[3pt] {{\rm{\;semi}} - {\rm{positive\;definite}}} & {}{ \Rightarrow {\rm{neutral\;equilibrium}}}\\[3pt] {{\rm{\;all\;other\;cases}}}& {}{ \Rightarrow {\rm{unstable\;equilibrium}}.}\end{array} \right. \end{align}
\begin{align}\frac{{{\partial ^2}{\Pi}}}{{\partial {{\bf{u}}^2}}} = { \boldsymbol{H}_{\Pi}}\left( \boldsymbol{u} \right) = {\boldsymbol{K}_T}\left( \boldsymbol{u} \right)\left\{ \begin{array}{rl}{{\rm{\;positive\;definite}}} & {} \Rightarrow {\rm{stable\;equilibrium}}\\[3pt] {{\rm{\;semi}} - {\rm{positive\;definite}}} & {}{ \Rightarrow {\rm{neutral\;equilibrium}}}\\[3pt] {{\rm{\;all\;other\;cases}}}& {}{ \Rightarrow {\rm{unstable\;equilibrium}}.}\end{array} \right. \end{align}
The definiteness of a matrix can be evaluated by looking at its eigenvalues. Consequently, we can recast Equation (7) as
 \begin{align}{ \boldsymbol{K}_T}\left( \boldsymbol{u} \right)\left\{ \begin{array}{rl}{{\rm{\;all\;eigen\;values\;}} \gt 0} & {}{ \Rightarrow {\rm{stable\;equilibrium}}}\\[3pt] {{\rm{\;all\;eigen\;values\;}} \geq 0} & {}{ \Rightarrow {\rm{neutral\;equilibrium^{3}}}}\\[3pt] {{\rm{\;atleast\;one\;eigen\;value\;}} \lt 0} & {}{ \Rightarrow {\rm{unstable\;equilibrium}}.}\end{array} \right. \end{align}
\begin{align}{ \boldsymbol{K}_T}\left( \boldsymbol{u} \right)\left\{ \begin{array}{rl}{{\rm{\;all\;eigen\;values\;}} \gt 0} & {}{ \Rightarrow {\rm{stable\;equilibrium}}}\\[3pt] {{\rm{\;all\;eigen\;values\;}} \geq 0} & {}{ \Rightarrow {\rm{neutral\;equilibrium^{3}}}}\\[3pt] {{\rm{\;atleast\;one\;eigen\;value\;}} \lt 0} & {}{ \Rightarrow {\rm{unstable\;equilibrium}}.}\end{array} \right. \end{align}
Equation (8) means that we can evaluate the nonlinear structural stability by monitoring the eigenvalues
![]() $\lambda $
of the tangent stiffness matrix at each converged increment of the nonlinear arc-length analysis. Since the tangent stiffness matrix of an FE model like the CRM-like Box Beam can be quite large, we only monitor the
$\lambda $
of the tangent stiffness matrix at each converged increment of the nonlinear arc-length analysis. Since the tangent stiffness matrix of an FE model like the CRM-like Box Beam can be quite large, we only monitor the
![]() ${N_\lambda } $
smallest magnitude eigenvalues, as monitoring all eigenvalues would be computationally impractical.
${N_\lambda } $
smallest magnitude eigenvalues, as monitoring all eigenvalues would be computationally impractical.
To investigate the nonlinear structural stability of the CRM-like Box Beam, we apply a load of magnitude twice as big as the linear buckling load,
![]() $P/{P_{{\rm{SOL}}105}} = 2 $
, and we monitor the 20 smallest eigenvalues of the tangent stiffness matrix. The analysis is carried out using MSC Nastran’s nonlinear solution sequence, SOL 106, and the arc-length method is implemented using the NLPARM and NLPCI cards. The parameters of these cards are set to trace the equilibrium path of the structure with suitably fine resolution. Their values are given in Table 3. The reader is referred to the MSC Nastran Quick Reference Guide for a detailed explanation on the meaning of the parameters.
$P/{P_{{\rm{SOL}}105}} = 2 $
, and we monitor the 20 smallest eigenvalues of the tangent stiffness matrix. The analysis is carried out using MSC Nastran’s nonlinear solution sequence, SOL 106, and the arc-length method is implemented using the NLPARM and NLPCI cards. The parameters of these cards are set to trace the equilibrium path of the structure with suitably fine resolution. Their values are given in Table 3. The reader is referred to the MSC Nastran Quick Reference Guide for a detailed explanation on the meaning of the parameters.
Table 3. Non-default parameters of the NLPARM and NLPCI Nastran cards employed for the nonlinear analysis of the CRM-like Box Beam

The 20 smallest eigenvalues of the tangent stiffness matrix are evaluated with an appropriate DMAP programme invoked by the Nastran input file. DMAP stands for Direct Matrix Abstraction Programme and it is a high-level language with its own compiler and grammatical rules that allows the user to modify MSC Nastran’s standard solution sequences to perform custom operations. The computation employs a Lanczos algorithm to find the eigenvalues for each converged increment.
The load-displacement diagram resulting from the nonlinear analysis is plotted in Fig. 11, in terms of the nondimensional applied load
![]() $P/{P_{{\rm{SOL}}105}} $
and of the root displacement
$P/{P_{{\rm{SOL}}105}} $
and of the root displacement
![]() ${u_{z,{\rm{\;}}455}} $
nondimensionalised with respect to the beam’s width
${u_{z,{\rm{\;}}455}} $
nondimensionalised with respect to the beam’s width
![]() $w $
. The load-displacement diagram depicts a broken supercritical pitchfork as the applied load approaches and exceeds
$w $
. The load-displacement diagram depicts a broken supercritical pitchfork as the applied load approaches and exceeds
![]() $P/{P_{{\rm{SOL}}105}} = 1 $
, a limit point bifurcation at
$P/{P_{{\rm{SOL}}105}} = 1 $
, a limit point bifurcation at
![]() $P/{P_{{\rm{SOL}}105}} = 1.42 $
, where the structure loses stability, and another limit point bifurcation at
$P/{P_{{\rm{SOL}}105}} = 1.42 $
, where the structure loses stability, and another limit point bifurcation at
![]() $P/{P_{{\rm{SOL}}105}} = 1.32 $
, where the structures recovers stability. The broken supercritical pitchfork appears because the bending load introduces a non-uniform compressive stress along the thickness of the top skin, making the problem asymmetric. The first limit point corresponds to an applied load that is
$P/{P_{{\rm{SOL}}105}} = 1.32 $
, where the structures recovers stability. The broken supercritical pitchfork appears because the bending load introduces a non-uniform compressive stress along the thickness of the top skin, making the problem asymmetric. The first limit point corresponds to an applied load that is
![]() $42{\rm{\% }} $
larger than the linear buckling load, clearly showing how the linear prediction places a glass ceiling on the structure’s limit load and prevents the exploitation of its full load-carrying capacity.
$42{\rm{\% }} $
larger than the linear buckling load, clearly showing how the linear prediction places a glass ceiling on the structure’s limit load and prevents the exploitation of its full load-carrying capacity.

Figure 11. Load-displacement diagram of the CRM-like Box Beam in terms of the displacement along the
![]() $z $
-axis of node 455.
$z $
-axis of node 455.
At this point, it is important to clarify that in a real wing structure material nonlinearity and plasticity can take place when exceeding the linear buckling load. This behaviour is not observed for the present structure because of the low load level that the structure is subjected to. In fact, by choosing as design load the linear buckling load of a wingbox structure with a uniform wall thickness distribution, this loads results much smaller than that that would result from an equal weight wingbox with an appropriate wall thickness distribution over its span. At the same time, this choice is beneficial to define an analysis and optimisation scenario that is completely driven by stability considerations, allowing to narrow the focus of this study.
The limit point bifurcation indicates that the structure would experience a snap when loaded past the limit point. Figure 12 shows the deformations before and after the snap. It is possible to observe a change of the deformation within the first rib bay: before the snap the deformation within each rib-stiffener bay is characterised by a single half-wave, while after the snap the deformation is characterised by two half-waves.

Figure 12. Deformation over the root of the CRM-like Box Beam before and after the snap-through. Displacements are amplified by a factor 50 for visualisation purposes. Elements are coloured by their average rotation about the
![]() $x $
-axis.
$x $
-axis.
As mentioned earlier, the stability of the equilibrium points shown in Fig. 11 is inferred from the eigenvalues of the tangent stiffness matrix. These are plotted in Fig. 13 against the nondimensional applied load, to assess their change as the structure is loaded. From the insets we can observe that all monitored eigenvalues remain positive along the broken supercritical pitchfork, that is to say around
![]() $P/{P_{{\rm{SOL}}105}} = 1 $
, while one eigenvalue becomes negative between the first and second limit point bifurcations, that is to say between a nondimensional applied load of
$P/{P_{{\rm{SOL}}105}} = 1 $
, while one eigenvalue becomes negative between the first and second limit point bifurcations, that is to say between a nondimensional applied load of
![]() $1.42 $
and
$1.42 $
and
![]() $1.32 $
.
$1.32 $
.

Figure 13. Smallest 20 eigenvalues of the tangent stiffness matrix, coloured from lowest to highest for each arc-length increment.
To assess the global effect of the nonlinear response shown in Fig. 11, we can plot the load-displacement diagram in terms of the tip displacement
![]() ${u_{z,{\rm{\;tip}}}} $
, as it is done in Fig. 14, where the displacement is nondimensionalised with the length
${u_{z,{\rm{\;tip}}}} $
, as it is done in Fig. 14, where the displacement is nondimensionalised with the length
![]() $l $
of the CRM-like Box Beam. In this case, the loss of stability at
$l $
of the CRM-like Box Beam. In this case, the loss of stability at
![]() $P/{P_{{\rm{SOL}}105}} = 1.42 $
appears hidden by the stable points. This suggests that looking only at the tip displacement and without monitoring the eigenvalues of the tangent stiffness matrix may be misleading for a structural analyst, as a limit point could not be immediately spotted. Finally, we can observe a change in the slope of the curve, corresponding to a global softening of the structure.
$P/{P_{{\rm{SOL}}105}} = 1.42 $
appears hidden by the stable points. This suggests that looking only at the tip displacement and without monitoring the eigenvalues of the tangent stiffness matrix may be misleading for a structural analyst, as a limit point could not be immediately spotted. Finally, we can observe a change in the slope of the curve, corresponding to a global softening of the structure.

Figure 14. Load-displacement diagram of the CRM-like Box Beam in terms of tip displacement.
The challenge of path-following
For the 1-DOF system of Section 2.2, it was shown that the broken supercritical pitchfork is made by two equilibrium paths: a stable natural path connected to the ground state and a partially stable and partially unstable complementary path disconnected from the ground state. The nonlinear response of the CRM-like Box Beam shown in Fig. 11, indicates the presence of a broken supercritical pitchfork and consequently suggests that one or more complementary paths may exist beyond the natural path shown in the figure.
We investigate the existence of equilibrium points that do not belong to the natural path by employing a coarse arc-length increment size, thereby allowing the nonlinear solver to jump away from the natural path to find equilibrium points on other paths. The coarse arc-length increments are implemented by setting default parameters for the NLPARM and NLPCI cards, except for the fields KMETHOD, KSTEP, TYPE, MAXITER and DESITER, which are kept as indicated in Table 3.
The results of the new nonlinear analysis are shown in Fig. 15 in terms of a 3D load-displacement diagram, where the root and tip displacements are plotted along the
![]() $x $
- and
$x $
- and
![]() $y $
-axis, respectively. The previously found natural path is also shown for comparison. We can observe that only the first two points lie on the natural equilibrium path, while all the others appear to belong to one or more complementary paths.
$y $
-axis, respectively. The previously found natural path is also shown for comparison. We can observe that only the first two points lie on the natural equilibrium path, while all the others appear to belong to one or more complementary paths.

Figure 15. Comparison of the 3D load-displacement diagram obtained with fine and coarse arc-length increment size.
To verify the existence of a complementary path, we unload the CRM-like Box Beam from the last equilibrium point of the analysis with coarse arc-length increments, setting the applied load to 0. The nonlinear analysis parameters of Table 3 are used to follow the unloading equilibrium path with a fine resolutionFootnote 4 and the results are shown in Fig. 16.

Figure 16. 3D load-displacement diagram obtained by unloading the structure from the last equilibrium point obtained from the analysis with coarse arc-length increments.
The structure is unloaded down to approximately
![]() $P/{P_{{\rm{SOL}}105}} = 0.87 $
, where the analysis stops because it reaches the maximum number of increments. However, we can clearly notice a jump from the complementary path to the natural path around
$P/{P_{{\rm{SOL}}105}} = 0.87 $
, where the analysis stops because it reaches the maximum number of increments. However, we can clearly notice a jump from the complementary path to the natural path around
![]() $P/{P_{{\rm{SOL}}105}} = 1.03 $
. Before this jump, the complementary path appears to be the ‘mirrored’ version of the natural path. In fact, we can observe the presence of a pair of load limit points between
$P/{P_{{\rm{SOL}}105}} = 1.03 $
. Before this jump, the complementary path appears to be the ‘mirrored’ version of the natural path. In fact, we can observe the presence of a pair of load limit points between
![]() $P/{P_{{\rm{SOL}}105}} = 1.29 $
and
$P/{P_{{\rm{SOL}}105}} = 1.29 $
and
![]() $1.32 $
. Except for the segment between these two limit points, the complementary equilibrium path appears to be completely stable.
$1.32 $
. Except for the segment between these two limit points, the complementary equilibrium path appears to be completely stable.
By examining Nastran’s output file, it is possible to notice that most arc-length increments converge within two or three iterations, whereas the increment where the jump occurs takes five iterations to converge. This finding suggests that the predictor step taken by the arc-length solver brings the system into the basin of attraction of the natural equilibrium path, and the successive iterations make the solver converge to a point on the natural path. For this reason, we repeat the analysis limiting the maximum number of iterations for each increment to 3Footnote 5 .
The results of this analysis are shown in Fig. 17. The solver follows the complementary path; a first limit point bifurcation is found and subsequently, the unstable segment of the path is successfully traversed past the second limit point bifurcation. When the solver approaches
![]() $P/{P_{{\rm{SOL}}105}} = 1 $
, the applied load increases and the equilibrium becomes unstable. This unstable part of the complementary path goes through a sequence of new load limit points. Interestingly, two islands of stability appear after the first two local maxima of the applied load. Instead, after the third local maximum of the applied load, the equilibrium path remains unstable, and the analysis stops at approximately
$P/{P_{{\rm{SOL}}105}} = 1 $
, the applied load increases and the equilibrium becomes unstable. This unstable part of the complementary path goes through a sequence of new load limit points. Interestingly, two islands of stability appear after the first two local maxima of the applied load. Instead, after the third local maximum of the applied load, the equilibrium path remains unstable, and the analysis stops at approximately
![]() $P/{P_{{\rm{SOL}}105}} = 1.40 $
because it reaches the maximum number of increments.
$P/{P_{{\rm{SOL}}105}} = 1.40 $
because it reaches the maximum number of increments.

Figure 17. 3D load-displacement diagram obtained by unloading the structure from the last equilibrium point obtained from the analysis with coarse arc-length increments using a maximum number of iterations for each increment equal to 3.
The analyses shown above are meant to give an idea of the challenges that can be encountered when path-following the equilibrium paths of a relatively complex structure such as a wingbox. The arc-length control method is needed to follow equilibrium paths with unstable points and sometimes a small increment size is required to prevent the solver from jumping between different paths. However, even a small increment size cannot always prevent the solver from jumping onto another path or from bouncing back at limit points.
As discussed by Groh et al. [Reference Groh, Avitabile and Pirrera36], generalised path-following methods can facilitate the analysis of complex nonlinear equilibrium paths by providing a more robust continuation approach. For instance, a potential solution to the demonstrated path-following issues could be the use of higher-order prediction methods for the arc-length solver, which are based on the idea of using the information related to a few, rather than just one, of the last converged points to obtain a more robust prediction of the next equilibrium point [Reference Eriksson37]. However, this is not an option when using closed-source commercial codes, such as MSC Nastran in this work. In fact, in the face of such a challenging task like the one described above, the availability of an open-source structural code allowing full control over the nonlinear solver would be ideal to tackle the problem. Instead, when working with closed-source commercial codes, the options are very limited, and the user has to use their creativity to make the most of the parameters that the commercial code offers to control the nonlinear analysis.
4.0 Optimisation of the CRM-like Box Beam with nonlinear structural stability constraints
In this section, a novel nonlinear structural stability constraint for aeroelastic optimisation is formulated and a simple structural optimisation is attempted to prove its validity.
The proposed nonlinear structural stability constraint is based on the idea of assessing the stability of the structure by monitoring the
![]() ${N_\lambda } $
smallest magnitude eigenvalues of the tangent stiffness matrix, as shown in Section 3. As stated in Equation (8), the structure is in a stable equilibrium when all eigenvalues of the tangent stiffness matrix are positive, and, as a consequence, the proposed constraint consists in imposing that the
${N_\lambda } $
smallest magnitude eigenvalues of the tangent stiffness matrix, as shown in Section 3. As stated in Equation (8), the structure is in a stable equilibrium when all eigenvalues of the tangent stiffness matrix are positive, and, as a consequence, the proposed constraint consists in imposing that the
![]() ${N_\lambda } $
eigenvalues monitored during the nonlinear analysis are always larger than zero.
${N_\lambda } $
eigenvalues monitored during the nonlinear analysis are always larger than zero.
The nonlinear stability constraint is tested in a structural optimisation of the CRM-like Box Beam, to verify its benefit over the traditional linear buckling approach. The objective function to be minimised is chosen to be the structural mass
![]() $m $
. To keep the optimisation problem simple, a single design variable is considered, corresponding to the wall thickness
$m $
. To keep the optimisation problem simple, a single design variable is considered, corresponding to the wall thickness
![]() $t $
, which is taken as a uniform value for all the elements of the structure. With this choice, a one to one relation between the wall thickness and the linear buckling load is obtained. In other words, for each value of wall thickness there is a corresponding value of linear buckling load predicted by SOL 105. It follows that when the CRM-like Box Beam is loaded with the linear buckling load corresponding to the value of its initial wall thickness, the structure is already optimal in linear buckling terms. The reason for this is that the wall thickness cannot be decreased while keeping the same applied load, because the linear buckling analysis would predict that the structure has failed in buckling. However, as demonstrated in Section 3, this glass ceiling placed by the linear analysis can be broken by means of a nonlinear analysis, which shows that the structure remains in a stable equilibrium far beyond the linear buckling load and consequently suggests that the wall thickness can be reduced without incurring into failure.
$t $
, which is taken as a uniform value for all the elements of the structure. With this choice, a one to one relation between the wall thickness and the linear buckling load is obtained. In other words, for each value of wall thickness there is a corresponding value of linear buckling load predicted by SOL 105. It follows that when the CRM-like Box Beam is loaded with the linear buckling load corresponding to the value of its initial wall thickness, the structure is already optimal in linear buckling terms. The reason for this is that the wall thickness cannot be decreased while keeping the same applied load, because the linear buckling analysis would predict that the structure has failed in buckling. However, as demonstrated in Section 3, this glass ceiling placed by the linear analysis can be broken by means of a nonlinear analysis, which shows that the structure remains in a stable equilibrium far beyond the linear buckling load and consequently suggests that the wall thickness can be reduced without incurring into failure.
For the reason described above, we choose the optimisation design load to be equal to the linear buckling load of the initial design,
![]() ${P_{{\rm{design}}}} = {P_{{\rm{SOL}}105,{\rm{\;}}0}} $
. Besides stability, we also require all deformations to be elastic, or in other words that the material does not yield. Finally, we need to impose that the applied load at the end of the nonlinear analysis,
${P_{{\rm{design}}}} = {P_{{\rm{SOL}}105,{\rm{\;}}0}} $
. Besides stability, we also require all deformations to be elastic, or in other words that the material does not yield. Finally, we need to impose that the applied load at the end of the nonlinear analysis,
![]() ${P_{{\rm{end}}}} $
, is equal to the design load, in order to avoid misleading the optimiser if the analysis does not converge to the prescribed load. In summary, the optimisation problem is defined as
${P_{{\rm{end}}}} $
, is equal to the design load, in order to avoid misleading the optimiser if the analysis does not converge to the prescribed load. In summary, the optimisation problem is defined as
 \begin{align} \begin{array}{l@{\quad}l@{\quad}l}{{\rm{minimise}}} {}& {}m {}& \\[3pt] {{\rm{by\;varying}}} {}& {}{{t_{{\rm{min}}}} \le t \le {t_{{\rm{max}}}}} {}&\\[3pt] {{\rm{subject\;to}}} {}& {}{{g_{\lambda, {\rm{\;}}ij}} = - {\lambda _{ij}} \lt 0} {}& {}{i = 1, \ldots, {N_i},{\rm{\;\;}}j = 1, \ldots, {N_\lambda }}\\[3pt] & {}{{g_{\sigma, {\rm{\;}}k}} = {\sigma _k} - {\sigma _{{\rm{max}}}} \lt 0} {}& {}{k = 1, \ldots, {N_e}}\\[3pt] & {}{{g_P} = 0.99 - \frac{{{P_{{\rm{end}}}}}}{{{P_{{\rm{design}}}}}} \lt 0,} {}& \end{array} \end{align}
\begin{align} \begin{array}{l@{\quad}l@{\quad}l}{{\rm{minimise}}} {}& {}m {}& \\[3pt] {{\rm{by\;varying}}} {}& {}{{t_{{\rm{min}}}} \le t \le {t_{{\rm{max}}}}} {}&\\[3pt] {{\rm{subject\;to}}} {}& {}{{g_{\lambda, {\rm{\;}}ij}} = - {\lambda _{ij}} \lt 0} {}& {}{i = 1, \ldots, {N_i},{\rm{\;\;}}j = 1, \ldots, {N_\lambda }}\\[3pt] & {}{{g_{\sigma, {\rm{\;}}k}} = {\sigma _k} - {\sigma _{{\rm{max}}}} \lt 0} {}& {}{k = 1, \ldots, {N_e}}\\[3pt] & {}{{g_P} = 0.99 - \frac{{{P_{{\rm{end}}}}}}{{{P_{{\rm{design}}}}}} \lt 0,} {}& \end{array} \end{align}
where
![]() ${t_{{\rm{min}}}} $
and
${t_{{\rm{min}}}} $
and
![]() ${t_{{\rm{max}}}} $
are the thickness bounds, which are set between 1 and 20mm,
${t_{{\rm{max}}}} $
are the thickness bounds, which are set between 1 and 20mm,
![]() ${\lambda _{ij}} $
is the
${\lambda _{ij}} $
is the
![]() $j $
-th tangent stiffness matrix eigenvalue at the
$j $
-th tangent stiffness matrix eigenvalue at the
![]() $i $
-th iteration,
$i $
-th iteration,
![]() ${\sigma _k} $
is the von Mises stress of the
${\sigma _k} $
is the von Mises stress of the
![]() $k $
-th element for the final applied load, evaluated at both the top and bottom plane of the element, and
$k $
-th element for the final applied load, evaluated at both the top and bottom plane of the element, and
![]() ${\sigma _{{\rm{max}}}} $
is the yield strength of the material.
${\sigma _{{\rm{max}}}} $
is the yield strength of the material.
The constraint on the applied load at the end of the nonlinear analysis is implemented as an inequality, where the difference with respect to the prescribed load must be smaller than
![]() $1{\rm{\% }} $
. As far as the other constraints are concerned, instead of imposing them on individual eigenvalues and elements, they are aggregated using the Kreisselmeier–Steinhauser (KS) functions [Reference Martins and Ning38]
$1{\rm{\% }} $
. As far as the other constraints are concerned, instead of imposing them on individual eigenvalues and elements, they are aggregated using the Kreisselmeier–Steinhauser (KS) functions [Reference Martins and Ning38]
 \begin{align}K{S_\lambda } = \mathop {{\rm{max}}}\limits_{i,j} \left( {{g_{\lambda, {\rm{\;}}ij}}} \right) + \frac{1}{\rho }{\rm{ln}}\!\left( {\mathop \sum \limits_{i = 1}^{{N_i}} \mathop \sum \limits_{j = 1}^{{N_\lambda }} {\rm{exp}}\!\left( {\rho\! \left( {{g_{\lambda, {\rm{\;}}ij}} - \mathop {{\rm{max}}}\limits_{i,j} \left( {{g_{\lambda, {\rm{\;}}ij}}} \right)} \right)} \right)} \right) \\[-24pt] \nonumber \end{align}
\begin{align}K{S_\lambda } = \mathop {{\rm{max}}}\limits_{i,j} \left( {{g_{\lambda, {\rm{\;}}ij}}} \right) + \frac{1}{\rho }{\rm{ln}}\!\left( {\mathop \sum \limits_{i = 1}^{{N_i}} \mathop \sum \limits_{j = 1}^{{N_\lambda }} {\rm{exp}}\!\left( {\rho\! \left( {{g_{\lambda, {\rm{\;}}ij}} - \mathop {{\rm{max}}}\limits_{i,j} \left( {{g_{\lambda, {\rm{\;}}ij}}} \right)} \right)} \right)} \right) \\[-24pt] \nonumber \end{align}
 \begin{align}K{S_\sigma } = \mathop {{\rm{max}}}\limits_k \left( {{g_{\sigma, {\rm{\;}}k}}} \right) + \frac{1}{\rho }{\rm{ln}}\!\left( {\mathop \sum \limits_{k = 1}^{{N_e}} {\rm{exp}}\!\left( {\rho \!\left( {{g_{\sigma, {\rm{\;}}k}} - \mathop {{\rm{max}}}\limits_k \left( {{g_{\sigma, {\rm{\;}}k}}} \right)} \right)} \right)} \right) \end{align}
\begin{align}K{S_\sigma } = \mathop {{\rm{max}}}\limits_k \left( {{g_{\sigma, {\rm{\;}}k}}} \right) + \frac{1}{\rho }{\rm{ln}}\!\left( {\mathop \sum \limits_{k = 1}^{{N_e}} {\rm{exp}}\!\left( {\rho \!\left( {{g_{\sigma, {\rm{\;}}k}} - \mathop {{\rm{max}}}\limits_k \left( {{g_{\sigma, {\rm{\;}}k}}} \right)} \right)} \right)} \right) \end{align}
where
![]() $\rho $
is the aggregation factor determining how close the KS function is to the maximum function, and it is set to
$\rho $
is the aggregation factor determining how close the KS function is to the maximum function, and it is set to
![]() $100 $
. This aggregation technique returns a single value for each constraint, representing an envelope of all the calculated quantities.
$100 $
. This aggregation technique returns a single value for each constraint, representing an envelope of all the calculated quantities.
Despite being a single-discipline problem, the optimisation is set up in the OpenMDAO framework [Reference Gray, Hwang, Martins, Moore and Naylor39] in view of a future extension to a coupled aeroelastic analysis. OpenMDAO is an open-source software framework for multidisciplinary design, analysis, and optimisation of complex systems. Among the optimisation algorithms available within the OpenMDAO architecture, the gradient-free Constrained Optimisation BY Linear Approximation (COBYLA) algorithm is chosen. COBYLA is a derivative-free optimisation method that constructs linear polynomial approximations of the objective and constraint functions [Reference Powell40]. The choice of a gradient-free algorithm is made both out of simplicity and because in the nonlinear structural stability optimisations the constraint on the applied load makes the constraint functions discontinuous, which can pose challenges for gradient-based methods. COBYLA is particularly well-suited for problems with nonlinear constraints and where gradient information is unavailable or unreliable. The pyNastran libraryFootnote 6 is utilised to interface the Nastran model with the OpenMDAO framework.
The challenge of path-following explained in Section 3 becomes even more arduous when it is applied to an optimisation problem. In fact, optimisation ideally requires a high-performance and robust structural code that can follow the natural equilibrium path in a computationally efficient manner and without jumping to other paths or bouncing back at limit points. This is in contrast with what was observed for MSC Nastran SOL 106, where robust path-following required a small arc-length increment size, which is not computationally efficient. To address this issue, several combinations of the nonlinear analysis parameters available in SOL 106 were tested. The most efficient strategy was found by starting the nonlinear analysis with a relatively large arc-length increment size, and then allowing the increment size to reduce as much as needed in presence of strong nonlinearities such as broken supercritical pitchforks and limit points. In fact, a fine resolution of the natural equilibrium path is only needed in those circumstances, and for small applied loads the path can be reliably followed with coarse resolution.
The described strategy is implemented by setting the default initial step size to
![]() $10{\rm{\% }} $
of the total applied load, and by constraining the maximum number of allowed Newton-Raphson iterations for each increment to 3. This choice ensures that the arc-length solver can easily converge in three iterations where the path is largely ‘straight’, while it is forced to bisect the increment size a number of times in presence of strong nonlinearities. The full list of the non-default parameters of the NLPARM and NLPCI cards adopted for the optimisation is given in Table 4.
$10{\rm{\% }} $
of the total applied load, and by constraining the maximum number of allowed Newton-Raphson iterations for each increment to 3. This choice ensures that the arc-length solver can easily converge in three iterations where the path is largely ‘straight’, while it is forced to bisect the increment size a number of times in presence of strong nonlinearities. The full list of the non-default parameters of the NLPARM and NLPCI cards adopted for the optimisation is given in Table 4.
Table 4. Non-default parameters of the NLPARM and NLPCI Nastran cards employed for the nonlinear analyses during the optimisation of the CRM-like Box Beam

The optimisation is performed on a Dell OptiPlex 5060 workstation and it takes 3.5 hours to complete. Only limited parallelisation is employed, setting SOL 106 to use shared memory parallel computation over four processors. The optimisation history is shown in Fig. 18. As it can be observed, the COBYLA algorithm does not guarantee to end the optimisation on a feasible design point, so we select the optimal design in correspondence of the last feasible iteration. At this design point, the structural mass is reduced by
![]() $10.9{\rm{\% }} $
, with the wall thickness decreasing from its initial value of
$10.9{\rm{\% }} $
, with the wall thickness decreasing from its initial value of
![]() $7.7{\rm{mm}} $
to a final value of
$7.7{\rm{mm}} $
to a final value of
![]() $6.9{\rm{mm}} $
, and with all constraints being satisfied within optimiser tolerances. As expected from the choice of the design load, we note that the constraint on nonlinear structural stability is active, in contrast to that on material failure, which is not active.
$6.9{\rm{mm}} $
, and with all constraints being satisfied within optimiser tolerances. As expected from the choice of the design load, we note that the constraint on nonlinear structural stability is active, in contrast to that on material failure, which is not active.

Figure 18. Optimisation history.
The load-displacement diagram of the optimised structure is shown in Fig. 19, both in terms of root and tip displacement, and it is compared with that of the initial structure. As far as the root displacement is concerned, it is possible to notice a broken supercritical pitchfork around
![]() $P/{P_{{\rm{design}}}} = 0.7 $
and the onset of a limit point bifurcation right at the design load. This response is analogous to the one shown in Fig. 11, only shifted towards a lower applied load. As far as the tip displacement is concerned, it can be observed that the optimised structure is globally softer than the initial design, as evidenced by the smaller slope of the load-displacement curve. This is expected given the reduced wall thickness and mass. It is also possible to notice that the difference in slope between the two curves appears to increase approaching the design load, meaning that geometrical nonlinearities are kicking in for the optimised structure and having an effect on its global stiffness. Furthermore, in both plots it can be observed that the chosen parameters of the NLPARM and NLPCI cards successfully managed to decrease the arc-length increment size where the equilibrium path required a finer resolution to be accurately followed.
$P/{P_{{\rm{design}}}} = 0.7 $
and the onset of a limit point bifurcation right at the design load. This response is analogous to the one shown in Fig. 11, only shifted towards a lower applied load. As far as the tip displacement is concerned, it can be observed that the optimised structure is globally softer than the initial design, as evidenced by the smaller slope of the load-displacement curve. This is expected given the reduced wall thickness and mass. It is also possible to notice that the difference in slope between the two curves appears to increase approaching the design load, meaning that geometrical nonlinearities are kicking in for the optimised structure and having an effect on its global stiffness. Furthermore, in both plots it can be observed that the chosen parameters of the NLPARM and NLPCI cards successfully managed to decrease the arc-length increment size where the equilibrium path required a finer resolution to be accurately followed.

Figure 19. Load-displacement diagrams of initial and optimised CRM-like Box Beam.
Finally, the linear buckling load of the optimised structure is calculated with SOL 105, and the result is displayed in the load-displacement diagram. As it can be observed in the figure, the linear buckling analysis places a glass ceiling on the limit load of the structure at 71% of the design load. In other words, the linear buckling approach would require a heavier structure to carry the design load, while in reality the structure optimised with the nonlinear structural stability constraint is capable of carrying the design load in a stable equilibrium and with elastic deformations, thus saving mass with respect to the linear buckling approach.
At this point, it is important to clarify that the ultimate aim of the proposed approach is not to design structures operating close to their nonlinear structural stability limit under normal conditions, such as cruise flight. In future work, a careful assessment will be necessary to understand what loss of structural stability implies for a more realistic optimisation scenario. This assessment will involve the inclusion of multiple loading conditions in the sizing process, the identification of the structural parts that become critical in those different conditions, the effect of the nonlinear structural stability constraints on cruise flight performance, and the evaluation of the stability margins needed to prevent structural failure in extreme scenarios such as gust encounters.
The deformation at the design load for both the initial and the optimised structures is shown in Fig. 20, where the colourmap indicates the average rotation of the elements about the
![]() $x $
-axis. From the colour pattern, it is possible to observe a buckled-like deformation over the root region of the optimised structure, even if in terms of displacements, the pattern is basically unnoticeable. The softening effect when approaching the design load observed in Fig. 19 can be ascribed to the emergence of this shape. In comparison, the initial structure barely shows the same type of deformation over the root region, and its colour pattern is more similar to a beam undergoing a linear deformation.
$x $
-axis. From the colour pattern, it is possible to observe a buckled-like deformation over the root region of the optimised structure, even if in terms of displacements, the pattern is basically unnoticeable. The softening effect when approaching the design load observed in Fig. 19 can be ascribed to the emergence of this shape. In comparison, the initial structure barely shows the same type of deformation over the root region, and its colour pattern is more similar to a beam undergoing a linear deformation.

Figure 20. Deformation at design load of initial and optimised CRM-like Box Beam. Elements coloured by their average rotation about the
![]() $x $
-axis.
$x $
-axis.
5.0 Conclusion
A novel nonlinear structural stability constraint for the optimisation of wingbox structures has been presented in this work. The theoretical principles on nonlinear structural mechanics underlying the proposed approach were introduced and demonstrated on three canonical examples featuring the supercritical pitchfork bifurcation, the broken supercritical pitchfork and the limit point bifurcation. Successively, the nonlinear structural stability of a reinforced box beam abstraction of the CRM wingbox, called CRM-like Box Beam, was investigated. It was shown that the natural equilibrium path of the structure comprises a broken supercritical pitchfork and a limit point bifurcation. The structure was demonstrated to be stable up to an applied load that is
![]() $42{\rm{\% }} $
larger than the linear buckling load, showing how the linear approach places a glass ceiling on the limit load that the structure can carry. A contribution to this large difference comes from the choice of the applied load for the considered structure, while for more realistic wing structures under more realistic loading conditions material nonlinearity would be likely to occur and limit the highlighted difference.
$42{\rm{\% }} $
larger than the linear buckling load, showing how the linear approach places a glass ceiling on the limit load that the structure can carry. A contribution to this large difference comes from the choice of the applied load for the considered structure, while for more realistic wing structures under more realistic loading conditions material nonlinearity would be likely to occur and limit the highlighted difference.
The existence of a complementary path disconnected from the ground state was also highlighted, depicting the challenges of following the equilibrium paths of a complex structure like a wingbox. The nonlinear structural stability constraint was then introduced into a simple structural optimisation of the CRM-like Box Beam. A mass reduction of
![]() $10.9{\rm{\% }} $
was found in comparison to the baseline structure, optimal in linear buckling terms, highlighting the potential of the proposed constraint for aeroelastic optimisation. Future developments will focus on the use of more design variables to obtain a varying distribution of thickness over the wingbox, the inclusion of non-conservative aerodynamic loading, and the use of a more realistic wingbox model.
$10.9{\rm{\% }} $
was found in comparison to the baseline structure, optimal in linear buckling terms, highlighting the potential of the proposed constraint for aeroelastic optimisation. Future developments will focus on the use of more design variables to obtain a varying distribution of thickness over the wingbox, the inclusion of non-conservative aerodynamic loading, and the use of a more realistic wingbox model.
Acknowledgments
This research was supported by Embraer S.A. and by the Engineering and Physical Sciences Research Council (EPSRC) via grant EP/T517872/1. The authors would like to thank Dr Mark Schenk from University of Bristol, whose course material provided inspiration for the canonical examples shown in this work, Mike Coleman from Coleman FEA Ltd. for his contribution to the development of the DMAP programme for the calculation of the eigenvalues of the tangent stiffness matrix, and Steven Doyle for his support with the pyNastran library.
Competing interests
The authors declare none.
A. Appendix
A.1 Derivation of canonical examples’ equilibrium equations
A.1.1 Supercritical pitchfork bifurcation
The total potential energy of the system shown in Fig. 1 is given by Equation (1), where the strain energy
![]() $U $
is given by
$U $
is given by
and the work
![]() $W $
done by the applied load
$W $
done by the applied load
![]() $P $
can be calculated as
$P $
can be calculated as
Substituting in Equation (1) we obtain the total potential energy in the form of
To calculate the equilibrium points, we need to apply Equation (2) such that
The above expression has a trivial solution for
![]() $\theta = 0 $
, corresponding to no displacement of the rods, and a non-trivial solution for
$\theta = 0 $
, corresponding to no displacement of the rods, and a non-trivial solution for
For the stability of the equilibrium points, we need to apply Equation (3) such that
For
![]() $\theta = 0 $
, the stability conditions are given by
$\theta = 0 $
, the stability conditions are given by
 \begin{align}\left\{ {\begin{array}{l}{\dfrac{{{\partial ^2}{\Pi}}}{{\partial {\theta ^2}}} \gt 0\;\;{\rm{for\;\;}}P \lt {P_{\rm{c}}}}\\[8pt] {\dfrac{{{\partial ^2}{\Pi}}}{{\partial {\theta ^2}}} \lt {0\;\;{\rm{for\;\;}}P} \gt {P_{\rm{c}}}}\end{array}} \right. \end{align}
\begin{align}\left\{ {\begin{array}{l}{\dfrac{{{\partial ^2}{\Pi}}}{{\partial {\theta ^2}}} \gt 0\;\;{\rm{for\;\;}}P \lt {P_{\rm{c}}}}\\[8pt] {\dfrac{{{\partial ^2}{\Pi}}}{{\partial {\theta ^2}}} \lt {0\;\;{\rm{for\;\;}}P} \gt {P_{\rm{c}}}}\end{array}} \right. \end{align}
where
![]() $P_{\rm{c}} = 2k/l $
is the critical buckling load, or in other words, the load where the second derivative of the potential energy is zero and where a bifurcation occurs.
$P_{\rm{c}} = 2k/l $
is the critical buckling load, or in other words, the load where the second derivative of the potential energy is zero and where a bifurcation occurs.
For
![]() $P = {P_{\rm{c}}}\theta /{\rm{sin}}\,\theta $
, the stability condition is
$P = {P_{\rm{c}}}\theta /{\rm{sin}}\,\theta $
, the stability condition is
which means that the equilibrium points described by Equation (5) are always stable.
A.1.2 Broken supercritical pitchfork
For the case of the rods at an initial angle
![]() ${\theta _0} $
shown in Fig. 3, the strain energy is calculated as
${\theta _0} $
shown in Fig. 3, the strain energy is calculated as
and the work done by the applied load is found as
Substituting into Equation (1), we obtain the total potential energy in the form of
and by applying Equation (2), we find the expression of the equilibrium points as
that can be rewritten in the form of
We then apply Equation (3) to assess the stability of the equilibrium points, such that
Substituting Equation (3) into Equation (4), we can obtain a suitable expression to evaluate the stability of the equilibrium points, thus
and find the stability conditions in the form of
 \begin{align}\left\{ {\begin{array}{l}{\dfrac{{{\partial ^2}{\Pi}}}{{\partial {\theta ^2}}} \gt 0\;\;\textrm{for}\;\;\dfrac{{\theta - {\theta _0}}}{{{\rm{tan}}\,\theta }} \lt 1}\\[7pt] {\dfrac{{{\partial ^2}{\Pi}}}{{\partial {\theta ^2}}} \lt {0\;\;\textrm{for}\;\;\dfrac{{\theta - {\theta _0}}}{{{\rm{tan}}\,\theta }}} \gt 1.}\end{array}} \right. \end{align}
\begin{align}\left\{ {\begin{array}{l}{\dfrac{{{\partial ^2}{\Pi}}}{{\partial {\theta ^2}}} \gt 0\;\;\textrm{for}\;\;\dfrac{{\theta - {\theta _0}}}{{{\rm{tan}}\,\theta }} \lt 1}\\[7pt] {\dfrac{{{\partial ^2}{\Pi}}}{{\partial {\theta ^2}}} \lt {0\;\;\textrm{for}\;\;\dfrac{{\theta - {\theta _0}}}{{{\rm{tan}}\,\theta }}} \gt 1.}\end{array}} \right. \end{align}
A.1.3 Limit point bifurcation
The strain energy of the inclined rods with elastic support shown in Fig. 5 is given by
The work done by the applied transverse load is calculated as
Substituting in Equation (1), we find the total potential energy as
and by applying Equation (2), we obtain the equilibrium equation of the system as
Rearranging the equation in terms of the load
![]() $P $
, we find that
$P $
, we find that
To assess the stability, we apply Equation (3), such that
We can then substitute the load
![]() $P $
with the equilibrium equation, thus
$P $
with the equilibrium equation, thus
 \begin{align} {\dfrac{{{\partial ^2}{\Pi}}}{{\partial {\theta ^2}}}} {}& = - 4k{l^2}\left( {{\rm{cos}}\,\theta - {\rm{cos}}\,{\alpha _0}} \right){\rm{cos}}\,\theta + 4k{l^2}{\rm{si}}{{\rm{n}}^2}\theta - 4kl\left( {{\rm{sin}}\,\theta - {\rm{cos}}\,{\alpha _0}{\rm{tan}}\,\theta } \right)l{\rm{sin}}\,\theta = \nonumber \\[3pt] & = 4k{l^2}\left( {{\rm{cos}}\,{\alpha _0}\left( {{\rm{cos}}\,\theta + {\rm{tan}}\,\theta {\rm{sin}}\,\theta } \right) - {\rm{co}}{{\rm{s}}^2}\theta } \right) = \nonumber\\[3pt] & = 4k{l^2}\dfrac{{{\rm{cos}}\,{\alpha _0} - {\rm{co}}{{\rm{s}}^3}\,\theta }}{{{\rm{cos}}\,\theta }} \end{align}
\begin{align} {\dfrac{{{\partial ^2}{\Pi}}}{{\partial {\theta ^2}}}} {}& = - 4k{l^2}\left( {{\rm{cos}}\,\theta - {\rm{cos}}\,{\alpha _0}} \right){\rm{cos}}\,\theta + 4k{l^2}{\rm{si}}{{\rm{n}}^2}\theta - 4kl\left( {{\rm{sin}}\,\theta - {\rm{cos}}\,{\alpha _0}{\rm{tan}}\,\theta } \right)l{\rm{sin}}\,\theta = \nonumber \\[3pt] & = 4k{l^2}\left( {{\rm{cos}}\,{\alpha _0}\left( {{\rm{cos}}\,\theta + {\rm{tan}}\,\theta {\rm{sin}}\,\theta } \right) - {\rm{co}}{{\rm{s}}^2}\theta } \right) = \nonumber\\[3pt] & = 4k{l^2}\dfrac{{{\rm{cos}}\,{\alpha _0} - {\rm{co}}{{\rm{s}}^3}\,\theta }}{{{\rm{cos}}\,\theta }} \end{align}
which results in the stability conditions given by
 \begin{align}\left\{ {\begin{array}{l}{\dfrac{{{\partial ^2}{\Pi}}}{{\partial {\theta ^2}}} \gt 0\;\;{\rm{for\;\;}}\dfrac{{{\rm{cos}}\,{\alpha _0} - {\rm{co}}{{\rm{s}}^3}\,\theta }}{{{\rm{cos}}\,\theta }} \gt 0}\\[7pt] {\dfrac{{{\partial ^2}{\Pi}}}{{\partial {\theta ^2}}} \lt 0\;\;{\rm{for\;\;}}\dfrac{{{\rm{cos}}\,{\alpha _0} - {\rm{co}}{{\rm{s}}^3}\,\theta }}{{{\rm{cos}}\,\theta }} \lt 0.}\end{array}} \right. \end{align}
\begin{align}\left\{ {\begin{array}{l}{\dfrac{{{\partial ^2}{\Pi}}}{{\partial {\theta ^2}}} \gt 0\;\;{\rm{for\;\;}}\dfrac{{{\rm{cos}}\,{\alpha _0} - {\rm{co}}{{\rm{s}}^3}\,\theta }}{{{\rm{cos}}\,\theta }} \gt 0}\\[7pt] {\dfrac{{{\partial ^2}{\Pi}}}{{\partial {\theta ^2}}} \lt 0\;\;{\rm{for\;\;}}\dfrac{{{\rm{cos}}\,{\alpha _0} - {\rm{co}}{{\rm{s}}^3}\,\theta }}{{{\rm{cos}}\,\theta }} \lt 0.}\end{array}} \right. \end{align}
A.2 Derivation of the CRM-like box beam model
The CRM-like Box Beam model presented in Section 3 and optimised in Section 4 is derived based on the data provided by Ref. Reference Martins and Ning38).

Figure A1. Comparison of the 3D load-displacement diagram obtained with original and refined mesh.
The length
![]() $l $
of the CRM-like Box Beam is taken as half the span of the CRM wingbox
$l $
of the CRM-like Box Beam is taken as half the span of the CRM wingbox
![]() ${b_{{\rm{wb}}}} $
, such that
${b_{{\rm{wb}}}} $
, such that
Since both the width
![]() ${w_{{\rm{wb}}}}(y) $
and the height
${w_{{\rm{wb}}}}(y) $
and the height
![]() ${h_{{\rm{wb}}}}(y) $
of the CRM wingbox vary along the span, a reference value for each is needed to develop a straight untapered box beam abstraction. The reference value of the wingbox width is found by dividing the wingspan by the wingbox aspect ratio
${h_{{\rm{wb}}}}(y) $
of the CRM wingbox vary along the span, a reference value for each is needed to develop a straight untapered box beam abstraction. The reference value of the wingbox width is found by dividing the wingspan by the wingbox aspect ratio
![]() $A{R_{{\rm{wb}}}} $
, thus
$A{R_{{\rm{wb}}}} $
, thus
The aspect ratio of the wingbox is defined as the ratio between the square of its span and its planform area
![]() ${S_{{\rm{wb}}}} $
, in the form of
${S_{{\rm{wb}}}} $
, in the form of
where the planform area is calculated as the integral of the width along the semi-span, such that
The distribution of wingbox width along the span,
![]() ${w_{{\rm{wb}}}}\left( y \right) $
, is inferred from the data reported by Ref. Reference Martins and Ning38).
${w_{{\rm{wb}}}}\left( y \right) $
, is inferred from the data reported by Ref. Reference Martins and Ning38).
The reference wingbox height is obtained by dividing the wingbox volume
![]() ${V_{{\rm{wb}}}} $
by the planform area, thus
${V_{{\rm{wb}}}} $
by the planform area, thus
The wingbox volume can be calculated as the integral of the cross-sectional area of the wingbox along the semi-span. In turn, the cross-sectional area at each spanwise station can be approximated with the area of the trapezium formed by connecting the two spars. Consequently the volume results in
where
![]() ${h_{{\rm{front}}}}\left( y \right) $
and
${h_{{\rm{front}}}}\left( y \right) $
and
![]() ${h_{{\rm{rear}}}}\left( y \right) $
are the spanwise distribution of the front and rear spar height, respectively. Also these quantities are inferred from the data reported by Ref. Reference Martins and Ning38).
${h_{{\rm{rear}}}}\left( y \right) $
are the spanwise distribution of the front and rear spar height, respectively. Also these quantities are inferred from the data reported by Ref. Reference Martins and Ning38).
The height of the stiffeners
![]() ${h_s} $
and the wall thickness
${h_s} $
and the wall thickness
![]() $t $
are taken as 1/10 and 1/100 of the CRM-like Box Beam height, respectively. The values obtained from the above relations are reported in Fig. 9.
$t $
are taken as 1/10 and 1/100 of the CRM-like Box Beam height, respectively. The values obtained from the above relations are reported in Fig. 9.
Since the mesh convergence study discussed in Section 3 is performed employing linear buckling analyses, the convergence of the mesh is verified in the nonlinear regime. To do this, two nonlinear analyses are performed, one using the original mesh resulting from the convergence study and another one using a refined mesh generated by choosing as target element length half the element length used for the original mesh. The applied load is set to twice the linear buckling load obtained for the original mesh to capture the nonlinear region of the structural response.
The results of these analyses are shown in Fig. A1 in terms of a 3D load-displacement diagram. The root displacement is evaluated for both models at the node where the linear buckling analysis predicts the maximum displacement for the critical buckling mode, that is to say node 455 for the model employing the original mesh and and node 1,362 for the model employing the refined mesh. It is possible to observe that the two analyses predict the same qualitative behaviour, suggesting that the original mesh is detailed enough to capture the nonlinear response of the CRM-like Box Beam. In quantitative terms, the final root and tip displacements are
![]() $3.5{\rm{\% }} $
higher and
$3.5{\rm{\% }} $
higher and
![]() $1.0{\rm{\% }} $
lower with respect to the model employing the refined mesh, respectively, while the applied load where the stability is lost is
$1.0{\rm{\% }} $
lower with respect to the model employing the refined mesh, respectively, while the applied load where the stability is lost is
![]() $4.3{\rm{\% }} $
higher.
$4.3{\rm{\% }} $
higher.