Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-22T10:36:10.260Z Has data issue: false hasContentIssue false
  • English
  • Français

On the effect of a swept-wing–plate junction flow on the lift and drag

Published online by Cambridge University Press:  04 July 2016

L. Bernstein  and
S. Hamid
L. Bernstein
Affiliation:
Department of Engineering, Queen Mary and Westfield College, London, UK
S. Hamid
Affiliation:
Department of Engineering, Queen Mary and Westfield College, London, UK
Get access Rights & Permissions [Opens in a new window]

Summary

Measurements have been made of the surface pressure distributions in the region of the junction between an untapered wing, of NACA 0015 section swept back at 20°, and a flat plate on which a turbulent boundary layer had developed, for several values of wing incidence. It is shown that the section lift coefficient of the wing diminishes, while the pressure drag coefficient increases, as the junction is approached. Oil-flow visualisations on the plate surface show the passage of the horseshoe-like vortex which forms when the retarded boundary layer flow separates as it approaches the leading-edge of the junction. Kinks in the isobars on the plate correlate with the trailing “legs” of this vortex. The surface flow visualisations also show that the turbulence in the junction region spreads onto the wing from the leading edge at an angle of about 10°.

A rotatable X-wire anemometer was used to make measurements of the mean velocity field and of five components of the Reynolds stress tensor, in the wake of the junction, with the wing at incidences of 0° and 9°. Log-law (Clauser) plots were used with the profiles Ū(Y) of longitudinal velocity to estimate the skin friction coefficient on the plate, though adjustments of the zero for Y were necessary to obtain a sensible fit. These corrections were often larger than can be readily explained, but the skin-friction values are consistent with the corresponding, measured velocity correlation, 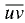. The Reynolds stresses in the wake region clearly show that the horseshoe-like vortex legs persist beyond the trailing-edge of the wing, the turbulence intensity being larger on the suction side for the wing at incidence.

Average values of the skin-friction coefficient on the plate in the junction region are little different from those away from the junction. No corresponding information is available for the skin-friction on the wing, but if this is likewise unaffected by the junction, then the total drag of the junction region will be greater than the sum of those of the isolated parts, simply because of the increase in pressure drag.

Type
Research Article
Information
The Aeronautical Journal , Volume 99 , Issue 987 , September 1995 , pp. 293 - 305
Copyright
Copyright © Royal Aeronautical Society 1995 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Carrier, G.F. The boundary layer in a corner, Quart App Maths, 1946, 4, pp 367–370.Google Scholar
2. El-Gamal, H.A. and Barclay, W.H. Experiments on the laminar flow in a rectangular streamwise corner, Aeronaut Q, 1978,29, pp 75–97.Google Scholar
3. Rubin, S.G. and Grossman, B. Viscous flow along a corner, Quart App Maths, 1971, 29, pp 169–186.Google Scholar
4. Zamir, M. and Young, A.D. Experimental investigation of the boundary layer in a streamwise corner, Aeronaut Q, 1970, 21, pp 313–339.Google Scholar
5. Shabaka, I.M.M.A. and Bradshaw, P. Turbulent flow measurements in an idealised wing-body junction, AlAA J, 1981,19, pp 131–132.Google Scholar
6. Baker, C.J. The laminar horse-shoe vortex, J Fluid Mech, 1979, 95, pp 347–367.Google Scholar
7. Baker, C.J. The turbulent horse-shoe vortex, J Wind Eng Ind Aero, 1980, 6, pp 9–23.Google Scholar
8. Baker, C.J. The position of points of maximum and minimum shear stress upstream of cylinders mounted normal to flat plates, J Wind Eng Ind Aero, 1985,18, pp 263–274.Google Scholar
9. Mehta, R.D. Effect of wing-nose shape on the flow in a wing/body junction, Aeronaut J, December 1984, 88, (880), pp 456-460.Google Scholar
10. Kubendran, L.R., Mcmahon, H.M. and Hubbartt, J.E. Turbulent flow around a wing/fuselage type juncture, AlAA J, 1986, 24, pp 1447–1452.Google Scholar
11. Devenport, W.J., Agarwal, N.K., Dewitz, M.B., SIMPSON, R.L. and PODDER, K. Effects of a fillet on the flow past a wing-body junction, AlAA J, 1990, 28, pp 2017–2024.Google Scholar
12. Devenport, W.J. and Simpson, R.L. Some time-dependent features of turbulent appendage-body juncture flows, 16th Symposium on Naval hydrodynamics, Berkeley, California, 1986.Google Scholar
13. Devenport, W.J. and Simpson, R.L. Turbulence structure near the nose of a wing-body junction, AlAA Paper 87-1310, 1987.Google Scholar
14. Devenport, W.J. and Simpson, R.L. LDV measurements in the flow past a wing-body junction. 4th International Symposium on Apps of Laser Anemometry to Fluid Mech, Lisbon, 1988.Google Scholar
15. Devenport, W.J. and Simpson, R.L. Time-dependent structure in wing-body junction flows, Turbulent Shear Flows VI, Springer-Verlag, 1989, pp 232–248.Google Scholar
16. Devenport, W.J. and Simpson, R.L. Time-dependent and time-aver aged turbulence structure near the nose of a wing-body junction, J Fluid Mech, 1990, 210, pp 23–55.Google Scholar
17. Devenport, W.J. and Simpson, R.L. The flow past a wing-body junction — an experimental evaluation of turbulence models, AlAA J, 1992, 30, pp 873–881.Google Scholar
18. Devenport, W.J., Simpson, R.L., Dewitz, M.B. and Agarwal, N.K. Effects of a strake on the flow past a wing-body junction, AlAA 29th Aerospace Sciences meeting, Reno, Nevada, AlAA Paper 91-0252, 1991.Google Scholar
19. Devenport, W.J., Simpson, R.L., Dewitz, M.B. and Agarwal, N.K. Effects of a leading-edge fillet on the flow past an appendage-body junction, AlAA J, 1992, 30, pp 2177–2183. (Revision of AlAA Paper 91-0252.)Google Scholar
20. Kubendran, L.R., Mcmahon, H.M. and Hubbartt, J.E. Interfer ence drag in a simulated wing-fuselage juncture, NASA CR-3811, 1984,58pp.Google Scholar
21. Kubendran, L.R., Bar-Sever, A. and Harvey, W.D. Flow control in a wing/fuselage type juncture, AlAA Paper 88-0614, 1988.Google Scholar
22. Mcmahon, H.M., Hubbartt, J.E. and Kubendran, L.R. Mean velocities and Reynolds stresses in a juncture flow, NASA CR-3605, 1982.Google Scholar
23. Mcmahon, H.M., Hubbartt, J.E. and Kubendran, L.R. Mean velocities and Reynolds stresses upstream of a simulated wing-fuselage juncture, NASA CR-3695, 1983.Google Scholar
24. Bernstein, L. and Hamid, S. An experimental investigation of wing/body junction flows, with and without a fillet, QMW Report EP 1095, 1993.Google Scholar
25. Gough, M.L. The effect of fillets between wings and fuselages on the drag and propulsion efficiency of an airplane, NACA TN 299, 1928.Google Scholar
26. Schlichting, H. Boundary layer theory, 7th edition, McGraw-Hill, 1979.Google Scholar
27. Gersten, K. Corner interference effects. AGARD report 299, 1959.Google Scholar
28. Arnott, A., Bernstein, L. and Petty, D.G. The aerodynamic inter action between a forward-swept wing and a plate, QMW Report ER 1016 for British Aerospace, commercial in confidence, 1993.Google Scholar
29. Mojola, O.O. Turbulent boundary layer along a streamwise corner, PhD thesis, University of London, 1972.Google Scholar
30. Sidal, R.C. and Davies, T.W. An improved response equation for hot-wire anemometry, J Heat and Mass Trans, 1972, 115, pp 367–368.Google Scholar
31. Johnston, L.J. Two-dimensional turbulent boundary layer/wake mixing, PhD thesis, University of London, 1986.Google Scholar
32. Bearman, P.W. Corrections for the effect of ambient temperature drift on hot-wire measurements in incompressible flow, NPL Aero Report 1302, 1969.Google Scholar
33. Rios-Chiquete, E. Unpublished data, Queen Mary College, University of London, 1982.Google Scholar
34. Fakas, E. and Bernstein, L. A new approach to adaptive-wall wind-tunnel testing, Aeronaut J, February 1994, 98, (972), pp 60–68.Google Scholar