Published online by Cambridge University Press: 12 August 2022
This paper consists of CFD and experimental study for shell projectile at angle of attack 00 and at various Mach numbers (0.7, 0.9, 1.0, 1.5 and 2.0), without spin effect. Passive method of base modification is used to reduce base drag. The goal of this study is to reduce base drag by utilising a base bleed approach called the Inward Turning Base Bleed Method (IWTB). The concept of IWTB is to draw relatively high-pressure air behind the driving band and allow it to pass through the bleed holes and direct it into the low-pressure base. This will in turn raise the base pressure and lower the base drag. The study comprises of (i) basic model with a boattail angle of
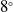 $8^{\circ}$
, (ii) eight different cavity models having different lip thickness and depth thickness ratios and (iii) nine different IWTB configurations for the optimised cavity model. At first, cavity model is optimised by varying the lip thickness and depth thickness ratio. Later IWTB parameters such as the bleed hole entry angles
$8^{\circ}$
, (ii) eight different cavity models having different lip thickness and depth thickness ratios and (iii) nine different IWTB configurations for the optimised cavity model. At first, cavity model is optimised by varying the lip thickness and depth thickness ratio. Later IWTB parameters such as the bleed hole entry angles
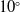 $10^{\circ}$
,
$10^{\circ}$
,
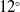 $12^{\circ}$
&
$12^{\circ}$
&
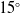 $15^{\circ}$
, exit bleed hole angles
$15^{\circ}$
, exit bleed hole angles
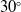 $30^{\circ}$
,
$30^{\circ}$
,
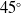 $45^{\circ}$
&
$45^{\circ}$
&
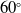 $60^{\circ}$
, bleed hole diameters 3mm, 4mm, 5mm & 6mm and number of bleed holes i.e., 4 & 8 were studied and optimised. Based on this study, the model with 8 holes, 3mm base bleed hole diameter,
$60^{\circ}$
, bleed hole diameters 3mm, 4mm, 5mm & 6mm and number of bleed holes i.e., 4 & 8 were studied and optimised. Based on this study, the model with 8 holes, 3mm base bleed hole diameter,
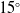 $15^{\circ}$
entry and
$15^{\circ}$
entry and
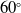 $60^{\circ}$
exit angle gives comparatively lower base drag. CFD result shows, in supersonic region the base drag reduction for optimised shell projectile is
$60^{\circ}$
exit angle gives comparatively lower base drag. CFD result shows, in supersonic region the base drag reduction for optimised shell projectile is
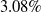 $3.08\%$
; at Mach number 0.9 the base reduction is
$3.08\%$
; at Mach number 0.9 the base reduction is
 $75.63\%$
; and in subsonic region it reduces to
$75.63\%$
; and in subsonic region it reduces to
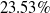 $23.53\%$
. CFD results were compared with experimental result, is found to be good and the differences lies within
$23.53\%$
. CFD results were compared with experimental result, is found to be good and the differences lies within
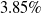 $3.85\%$
.
$3.85\%$
.