Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-21T14:55:20.056Z Has data issue: false hasContentIssue false
  • English
  • Français

Further Comments on Pontryagins Maximum Principle Applied to the Profile of a Beam

Published online by Cambridge University Press:  04 July 2016

L. C. W. Dixon
L. C. W. Dixon*
Affiliation:
Department of Mathematics, Lanchester College of Technology, Coventry
Get access Rights & Permissions [Opens in a new window]

Extract

Following the appearance of my note on this subject in the July 1967 JOURNAL, Professor Hemp kindly pointed out a mistake in one of the basic assumptions. This has led to a recalculation of the results, and the correct results are given below.

a width of beam

b lower bound on height of beam

d upper bound on height of beam

E Modulus of elasticity

h (x) height of beam at position x

H the Pontryagin Hamiltonian

i second moment of area=ah3/12

i length of beam

M (x) bending moment =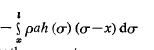

rl, r2non-dimensional length parameters

p density al lengthparam

t non-dimensional length parameter=x/l

u non-dimensional length parameter=h/l

x horizontal distance from base of beam

y (x) vertical displacement of the centre-line of beam

Y error function in hill climbing sequence

Vectors

f phase space velocity vector =dX/dt

P adjoint vector

X non-dimensional state vector

Type
Technical Notes
Information
The Aeronautical Journal , Volume 72 , Issue 690 , June 1968 , pp. 518 - 519
Copyright
Copyright © Royal Aeronautical Society 1968 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Dixon, L. Pontryagin's Maximum Principle Applied to the Profile of a Beam. J of Royal Aeronautical Soc, pp 513–515, July 1967.Google Scholar
2. Hemp, W. S. Private Communication, 1967.Google Scholar
3. Knapp, and Frost, . Determination of Optimal Control and Trajectories using the Maximum Principle in Association with a Gradient Technique, IEEE Trans Auto Control, Vol AC-10, No 2, 1966.Google Scholar
4. Rosenbrock, H. H. An automatic method for finding the greatest of least value of a function. Computer Journal, Vol 3, 1960.Google Scholar
5. Powell, M. J. D. An iterative method for finding stationary values of a function of several variables. Computer Journal, Vol 5, 1964.Google Scholar
6. Bellamy, N. W. and West, M. J. Methods of profile optimization by iterative analogue computation. (To be published.) Google Scholar