NOMENCLATURE

$\diameter$

Diameter [mm]

c

Thermal capacity [J kg⁻¹ K]

H

Enthalpy [MJ kg⁻¹]

k

Turbulent kinetic energy [m² s⁻²]

$k_T$

Thermal conductivity [Wm⁻¹ K]

M

Mach number [−]

P

Pressure [Pa]

$q,\,Q$

Heat flux [kWm⁻²]

t

Time [s]

T

Temperature [K]

u

Velocity [m s⁻¹]

V

Voltage [V]

Greek symbols

$\alpha_{fin}$

Fin angle [deg]

$\alpha_R$

TFHG sensitivity [K⁻¹]

$\delta$

Boundary layer thickness [mm]

$\eta$

Efficiency

$\rho$

Density [kgm⁻³]

Subscripts

0

Stagnation

ST

Shock Tube

$\infty$

Free stream

inj

Injector

mix

Mixing

w

Wall

2.0 T4 REFLECTED SHOCK TUBE TUNNEL

The T4 Stalker Tube is a free-piston reflected shock tube at the University of Queensland. Commissioned in 1987^{(Reference Doherty19)} from the design of Stalker^{(Reference Stalker20)}, the tunnel is capable of a total enthalpy range of 2.5-15.0MJ/kg^{(Reference Doherty19)} at a variety of Mach numbers^{(Reference Tanimizu21)}, currently with nozzles for nominal Mach numbers of $4.0$, $7.0$, $7.6$, and $10.0$. The nozzle supply pressure ranges between $10{}\sim90 \mathrm{MPa}$. This high-enthalpy impulse facility is usually run in a direct connect^{(Reference Kirchhartz22,Reference Ridings23)} or semi free-jet configuration^(9.24) due to the relatively small core size of the facility^{(Reference Itoh, Ueda, Komuro, Sato, Tanno and Takahashi25,Reference Stalker, Paull, Mee, Morgan and Jacobs26)} .

Able to achieve test times on the order of 1ms^{(Reference Stalker, Paull, Mee, Morgan and Jacobs26)}, this facility has been used extensively for scramjet propulsion/high-speed aerodynamic research^{(Reference Hunt, Paull, Boyce and Hagenmaier27,Reference Wise and Smart28)} . Figure 1 shows a generic overview of the facility with reference^{(Reference Doherty19)} containing an extensive description of the facility for the interested reader.

Figure 1. Schematic of the T4 Stalker Tube. Extracted from^{(Reference Doherty19)}.

3.0 EXPERIMENTAL MODEL

Figure 2(a) shows the canonical geometry used in the tests, consisting of a flat plate and a normal fin at an angle-of-attack used to generate scramjet-inlet like vortices. In the figure, the axial freestream moves in the positive X direction. Figure 2(b) shows a slice normal to the flow and illustrates how the vortex is generated by the shock-viscous interactions. The resulting vortex is equivalent to those generated in the inlet of non-axisymmetric scramjets^{(Reference Llobet, Gollan and Jahn16,Reference Llobet, Barth and Jahn17)} , where differing compression rates between ramp and sidewalls lead to similar interactions.

Figure 2. Test geometry and vortex flowfield structure depiction. Extracted from^{(Reference Llobet, Gollan and Jahn29)}

Figure 3 shows the model used in the experimental campaign. To ensure the model creates representative vortices, the Q factor was used to extract the vortex core location, size (defined as the region with $Q > 0.5 \, Q_{max \, at \, core}$), and intensity from these simulations^{(Reference Llobet, Jahn and Gollan15,Reference Llobet18)} . Setting the fin angle to $10^{\circ}$, and simulating a geometry equivalent to Fig. 3 at free stream conditions close to the experimental conditions resulted in representative vortices with a vortex intensity of 0.48. This vortex intensity is very similar to the values found in simulations of 2D scramjet geometries tested in T4 and the X3 expansion tube at UQ^{(Reference Llobet, Jahn and Gollan15,Reference Llobet18)} .

Figure 3. Experimental model for measuring jet-vortex induced heat transfer.

The width of the model/plate was 220 mm, which was selected to reduce the potential of any three-dimensional effects reaching the measurement area. The length of flat plate upstream of the fin leading edge was limited to 156mm due to the potential interference with the tunnel nozzle walls. The injector has a diameter of 1mm and is located 126mm downstream of the fin leading edge and inclined at ${45}^{\circ}$ relative to the axial flow direction. The injector is supplied with gaseous hydrogen from a plenum mounted below the plate. The plenum is fed by a Ludwieg tube at room temperature to maintain a constant total pressure during the test duration.

To test different injection locations, corresponding to different locations within the vortex, the fin can be translated in the model Y axis, as shown in Fig. 3(b).

To measure heat transfer downstream of the injector, Thin-Film Heat-transfer Gauges (TFHG) are arranged along five parallel lines as shown in Fig. 3(b). Each line of gauges contains 11 TFHGs that were manufactured at the Centre for Hypersonics at the University of Queensland. Each gauge consists of an approximately 20 nm thick nickel resistive strip element that is sputtered onto an optically smooth quartz substrate and shielded with a layer of $SiO_2$. The gauges are individually calibrated after manufacture following the procedure by Wise^{(Reference Wise24)}. Heat flux is calculated using Eq. 1, following the procedure from Schultz^{(Reference Wise24,Reference Schultz and Jones30)} , which integrates the change in voltage across the TFHG driven by a constant current source. $\rho$, c, $k_T$ are the properties of the substrate and $\alpha_R$ is the resistance-independent calibrated TFHG sensitivity.

(1)\begin{equation}\dot{q}_n = \frac{\sqrt{\rho \, c \, k_T}}{\sqrt{\pi}\alpha_R V_0}\sum^n_{i=1}\frac{V\!\left(t_0\right)-V\!\left(t_{i-1}\right)}{\left(t_n-t_i\right)^{1/2}+\left(t_n-t_{i-1}\right)^{1/2}}\end{equation}

The theoretical uncertainty for the TFHG heat flux measurements, considering material property variations, voltage measurement, and calibration uncertainties is $\pm {5.8}{\%}$^{(Reference Wise24)}. However, due to fabrication flaws and/or mounting imperfections this value was found to underpredict the actual uncertainty. For this reason, the uncertainty was calculated by comparing the average heat flux value measured from multiple TFHGs during a fuel off flat plate configuration experiment (no injection and fin removed). The resulting TFHG 95% confidence interval is $\pm {30}{\%}$, calculated using t-Student distribution for a population of 10 gauges^{(Reference Llobet18)}.

Figure 4. Stanton number for the TFHG’s in the boundary layer measurement region^{(Reference Llobet18)}. Theoretical laminar and turbulent Stanton number values calculated with the Cebeci Boundary Layer Code^{(Reference Cebeci and Bradshae31)}.

Figure 3(b) shows the TFHG sensor field that was employed to resolve the heat-transfer profile for the vortex-injection interaction. This arrangement was selected based on analysis presented in^{(Reference Llobet, Gollan and Jahn29)}. The gauges centers are separated by 4mm in the Y direction, while the lines are separated by 24.15mm in the X direction (or freestream direction). Moreover, the gauge lines have a 4.5mm offset in the positive Y direction in order to improve the sensor coverage. The first TFHG line is 12mm downstream of the injector.

Additionally, the model incorporates six TFHG on the farthest region of the flat plate from the fin, as shown in Fig. 3(c). These gauges measure and identify the state of the undisturbed boundary layer in the vicinity of the fin leading edge and injection location. These gauges are grouped in two sets of three, 10 mm apart. The first set starts at 143mm and is at the same axial location as the fin leading edge. The second set starts at 249mm and is located just upstream of the injector. Both sets of gauges are located far enough away from the fin that they are not affected by the oblique shock-wave or vortex.

The state of the boundary layer at both locations is determined by comparing the Stanton number calculated from the experimental measurements to the Cebeci Boundary Layer Code^{(Reference Cebeci and Bradshae31)}. The results shown in Fig. 4, show that the measurements correlate with the Stanton number for laminar flow, indicating that the undisturbed flow across the flat plate remains laminar.

Two flush mounted pressure tappings, using Kulite sensors, are incorporated in the flat plate to measure the free-stream static pressure upstream and downstream of the fin shock during the experiment.

3.1 T4 test flow conditions

The experiments were performed using the T4 Mach 7.6 nozzle at a Mach 8 flight-enthalpy. The nozzle exit flow conditions are derived from measurements of the shock tube fill pressure $\left(P_{ST}\right)$, shock tube shock-speed $\left(u_{S}\right)$, shock tube temperature $\left(T_{ST}\right)$, and the stagnation region nozzle supply pressure $\left(P_e\right)$. Uncertainties in the flow conditions are obtained by assuming the measured quantities are independent and normally distributed, and evaluating the sensitivities of the derived quantities to changes in the measured quantities^{(Reference Khang9,Reference Mee32)} . Table 1 summarises the calculated nozzle exit conditions along with their uncertainties.

Table 1 Nominal conditions during testing a nozzle exit

The nozzle exit conditions in Table 1 are calculated using the UQ in-house code NENZFr^{(Reference Doherty, Chan, Jacobs, Zander, Gollan and Kirchhartz33)}. NENZFr is a wrapper that integrates an ESTCj^{(Reference Jacobs, Gollan, Potter, Zander, Gildfind, Blyton, Chan and Doherty34)} shock-tube simulation into a space-marched thermal and chemical non-equilibrium simulation of the nozzle using the Eilmer CFD code. Eilmer3 is a collection of programs for the simulation of 2-D/3-D thermal and chemical non-equilibrium transient flows, developed at the UQ^{(Reference Gollan and Jacobs35)} and extensively validated for hypersonic flows.

The axisymmetric grid used for the space-marched Eilmer3 simulation is constructed by inscribing a uniform structured grid between a Bezier curve defining the nozzle wall and the nozzle centerline. The mesh employed in this study consisted of 600 by 40 elements in the axial and radial directions respectively. The chemical composition of the gas is calculated using finite-rate reactions with a five species air model: $N_2$, $O_2$, NO, N and O. The thermodynamic properties are obtained using NASA CEA2^{(Reference McBride and Gordon36)}.

Moreover, to improve the accuracy of the nozzle exit conditions, an iterative approach is applied to determine the transition location in the nozzle. The baseline predictive value is iterated until a satisfactory solution is found that agrees with the experimentally measured static pressure on the model plate. The uncertainty of this static pressure measurement is lower than the resultant sensitivity from the nozzle transition location, and thus is considered a truth value target for the iterative convergence^{(Reference Doherty19)}.

4.0 TEST CASES

Two experimental arrangements, corresponding to the fin being translated along the Y axis as depicted in Fig. 3(b) were tested. Moving the fin adjusts the relative position between the jet and vortex, and allows the effect of injector placement relative to the vortex to be observed. The fin locations are defined by the distance between jet and fin in the Y direction, non-dimensionalised by the jet diameter. The two arrangements have a fin-to-injector distance of $26.2 \, \diameter_{inj}$ and $35.2 \, \diameter_{inj}$, and are labeled Upper Fin (UF), and Lower Fin (LF) respectively.

Three tests were performed for each arrangement. The initial test uses No Injection (NI) and is used to obtain baseline heat flux data corresponding to an undisturbed vortex. For the other two tests hydrogen is injected with measured injector plenum pressures of approximately $P_{inj}={1300}{\text{kPa}}$ and $P_{inj}={430}{\text{kPa}}$. As the plenum and Ludwieg tube are at room temperature, a stagnation temperature of 300 K is assumed for all tests. These two tests are labeled High Injection (HI) and Low Injection (LI) respectively. These injections pressures result in injection-to-free-stream momentum ratios of approximately (J) of $5.24$, and $1.73$. The resulting six experimental configurations are summarised in Table 2.

Table 2 Combination of injection conditions and fin position for the different test cases

5.0 CFD REFERENCE RESULTS

The data obtained in the experiments is complemented with numerical simulations to enhance the understanding of the results and assess the validity of the numerical methodology. The CFD solver used is US3D, developed at the University of Minnesota^{(Reference Nompelis, Drayna and Candler37)}. Steady state RANS simulations using non-reacting flow and the SST turbulence model with a Schmidt number (Sc) of 0.7 are performed. The typical near-wall cell size is 2 µm, keeping the y+ values below 1 for the whole domain, except for the first few cells adjacent to the fin leading edge. The Steger-Warming flux vector splitting method is used for the convective fluxes. In regions of strong shocks, the MUSCL scheme with pressure limiter is used. The implicit time integration uses the DPLR method^{(Reference Wright, Candler and Bose38)}. The typical value for CFL number is 50 towards the end of the simulations.

The numerical domain spans from 10 mm upstream to 300 mm downstream of the fin leading edge and 200 mm in the spanwise direction. The boundary layer development over the first 146mm of the flat plate upstream of the fin leading edge was calculated in a separate quasi two-dimensional simulation with an infinitely sharp leading edge. The exit profile from this simulation is used as the inflow boundary condition for the three-dimensional numerical domain described above. The walls are modeled as non-slip isothermal walls with a temperature of 300 K, the mean for the laboratory in which the experiments were conducted.

The structured three-dimensional domain contains approximately four million cells and has a minimum spacing in the vicinity of the injector of approximately 0.05mm. The cell growth from the injector is restricted to 1mm in the region of uniform flow and is considered an appropriate limit to resolve the far-field of the vortex-injection interaction. The meshes use a typical near-wall cell size of 2 µm, keeping the $y^+$ value below 1. Halving $y^+$ produced a 3% change in heat flux in the region of interest. The meshes used in the current study are equivalent to the ones used in a previous numerical study^{(Reference Llobet, Gollan and Jahn16)}, which includes a grid dependency study investigating several key parameters for vortex-injection interactions, such as mixing efficiency and penetration. Grids using approximately 3.8 to 4.0 million cells depending on the volume of the domain were found to be adequate.

Table 3 GCI for mixing efficiency and maximum penetration 1 to 3 from finer to coarser

This level adequately captures the main flow features as demonstrated in the prior work by comparing three levels (3.8, 7.6, 16.2 million cells) of refinement^{(Reference Llobet, Gollan and Jahn16)}. Moreover, the Grid Convergence Index (GCI) values^{(Reference Roache39)}, based on mixing efficiency $\left(\eta_{mix}\right)$ at two locations downstream of the injector, and maximum penetration were calculated and are reproduced in Table3. The GCI values for mixing efficiency near the injector ($\eta_{mix}\mid_{x=0.05}$) has relatively poor values due to the large concentration gradients in this region. Nonetheless, the GCI value improves further downstream, where the most relevant data is extracted. These values of mixing efficiency ($\eta_{mix}$) are obtained by analysing the flow over planes normal to the axial direction. On each plane, the mixing efficiency is calculated using Equation (2)^{(Reference Lee40)}, where $\rho$, u, and $c^{stoic}_{H2}$ are the density, axial velocity, and stoichiometric hydrogen ($H_2$) mass fraction.

(2)\begin{equation}\eta_{mix} = \frac{\int\int c^{r}_{H2} \cdot \rho \cdot u \cdot dy dz}{\int\int c_{H2}\cdot \rho \cdot u \cdot dy dz}\mbox {where} \quad \quad {c^{r}_{H2}} = \begin{cases} c_{H2} & c_{H2}\leq c^{stoic}_{H2} \\[3pt] \frac{1-c_{H2}}{1-c^{stoic}_{H2}} & c_{H2}> c^{stoic}_{H2}\end{cases}\end{equation}

The inflow conditions used for the simulations are the nominal conditions calculated at the nozzle exit from Table 1. Stanton number over the plate, as presented in Fig. 4, shows the flow remains fully laminar upstream of the oblique shock and injector. This also agrees with the transition predictions for the T4 tunnel from He and Morgan^{(Reference He and Morgan41)}. Thus, the pseudo-2D simulations to resolve the boundary layer development were conducted as fully laminar.

In the three-dimensional domain the RANS equations are closed with the SST $k-\omega$ turbulence model. This ensures turbulent mixing of the fuel and the production of turbulence in the boundary layer region separated by the fin shock is simulated satisfactorily. In order to accommodate the laminar inflow from the quasi-2D simulation, the Turbulent Kinetic Energy (TKE) at the inlet to the domain is set to zero. This replicates the laminar nature of the flow upstream of the fin, to match the experimental data shown in Fig. 4. More importantly, using a zero TKE inflow with the SST $k-\omega$ model, allows for an appropriate modeling of the viscous turbulence generation in the laminar boundary layer at the interaction with the fin shock, as well as turbulence generation in the separations and vortex-injection interaction.

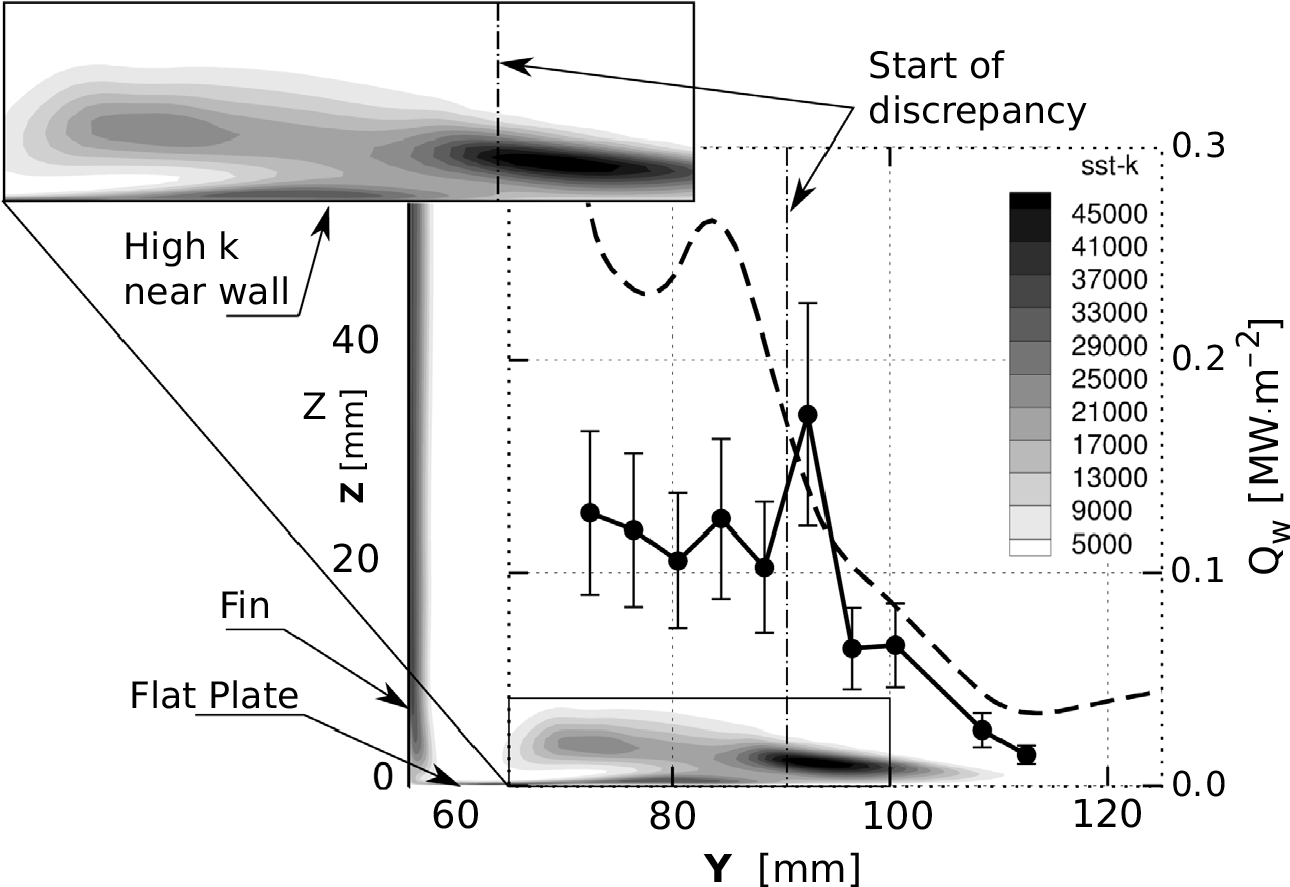
Figure 5a shows contours of TKE for the flow domain. From these contours the generation of turbulence downstream of the separation line and further generation surrounding the fuel jet is clearly evident. For a quantitative comparison TKE and heat flux was extracted along the dashed line TKE Extraction line shown in Fig. 5a. Examining the trace of TKE inset in Fig. 5a, it is evident that TKE remains negligible until just downstream of the injector, when a rapid increase occurs, with TKE stabilising at a higher level downstream of approximately $x = {400}{\text{mm}}$. Considering the heat flux from simulation and experiments, shown in Fig. 5b, again good agreement is seen for $x < {300}{\text{mm}}$, at which point the CFD simulations predict a rapid increase in heat transfer.

Figure 5. TKE and heat transfer from reference simulation to assess accuracy of boundary layer state prediction.

As in the experimental case, the flow upstream of the injector is laminar. Therefore, the swept shock interacts with a laminar boundary layer to generate the corner vortex. Further downstream, the transition to turbulent boundary layer in CFD introduces a deviation from the experimental case, where the boundary layer unaffected by the vortex remains laminar much longer. This deviation is only relevant in the region outside of the vortex, and thus is not relevant to the aim of this discussion. Nonetheless, the region where this discrepancy between CFD and experimental data is visible is briefly described in subsequent sections for completeness.