Published online by Cambridge University Press: 09 August 2019
Concepts of new fluttering wind and water mills led to general solution of flutter by a foil section free to pitch about an axis ahead of 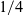 ${1}/{4}$
chord. The pitch damping of the vorticity being shed by lift change is negative singular via the imaginary part of the Theodorsen function. So a 2D airfoil can slowly flutter in pure pitch at a very high inertia with radian frequency and growth rate, reduced by windspeed/chord, resp. less than .087 and .01. At the frequency of nil net pitch damping, the binary inertia/damping cross determinant vanishes on a line in the imbalance vs inertia plane. The perturbed frequency contours just a bit above and below this ‘beab’ line spectacularly split to asymptote to the pure pitch inertia vertical of implied infinite heave stiffness. Higher frequency contours turn back towards the positive imbalance axis and then the origin, changing from hyperbolic to elliptical at exactly the same .087 and asymptoting to a line between the nexus and four times the nexus and a mode of effective pitch about
${1}/{4}$
chord. The pitch damping of the vorticity being shed by lift change is negative singular via the imaginary part of the Theodorsen function. So a 2D airfoil can slowly flutter in pure pitch at a very high inertia with radian frequency and growth rate, reduced by windspeed/chord, resp. less than .087 and .01. At the frequency of nil net pitch damping, the binary inertia/damping cross determinant vanishes on a line in the imbalance vs inertia plane. The perturbed frequency contours just a bit above and below this ‘beab’ line spectacularly split to asymptote to the pure pitch inertia vertical of implied infinite heave stiffness. Higher frequency contours turn back towards the positive imbalance axis and then the origin, changing from hyperbolic to elliptical at exactly the same .087 and asymptoting to a line between the nexus and four times the nexus and a mode of effective pitch about 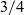 ${3}/{4}$
chord. At .6 the pure pitch frequency the imaginary part dominates in the quadratic inertia and imbalance coefficients to bend the neutral contours down and across the quasi-steady line to even turn back to very large negative imbalance at small inertia, where kinematics then imply high mass. Diagonally mirror hyperbolae exist for greater than the pure pitch inertia with a different dynamic implication of very high foil mass.
${3}/{4}$
chord. At .6 the pure pitch frequency the imaginary part dominates in the quadratic inertia and imbalance coefficients to bend the neutral contours down and across the quasi-steady line to even turn back to very large negative imbalance at small inertia, where kinematics then imply high mass. Diagonally mirror hyperbolae exist for greater than the pure pitch inertia with a different dynamic implication of very high foil mass.