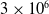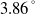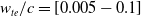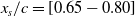Nomenclature
- a
-
speed of sound
- c
-
chord length of the aerofoil
-
 $C_d$
$C_d$
-
drag coefficient
-
 $C_l$
$C_l$
-
lift coefficient
-
 $C_p$
$C_p$
-
pressure coefficient
-
 $GCI_{i,i+1}$
$GCI_{i,i+1}$
-
grid convergence index between grid i and
 $i+1 (-)$
$i+1 (-)$
- M
-
mach number
- p
-
pressure
- Re
-
reynolds number
- t
-
time
-
 $Tu_{far}$
$Tu_{far}$
-
turbulence intensity
-
 $u_i=(U,V,W)$
$u_i=(U,V,W)$
-
velocity vector
-
 $w_{te}$
$w_{te}$
-
maximum deflection
- x,y
-
Cartesian coordinates
-
 $x_s$
$x_s$
-
start morphing location
-
 $y_c$
$y_c$
-
camber line of morphing aerofoil
-
 $y_t$
$y_t$
-
thickness of baseline aerofoil
-
 $y^+$
$y^+$
-
non-dimensional spacing from aerofoil surface to the first mesh node
Greek symbol
-
 $\alpha$
$\alpha$
-
angle-of-attack
-
 $\theta$
$\theta$
-
local slope of morphing aerofoil
-
 $\mu$
$\mu$
-
kinematic viscosity
-
 $\mu_t$
$\mu_t$
-
turbulent viscosity
-
 $\rho$
$\rho$
-
density
1.0 Introduction
Since the beginning of aviation history, systems that change the camber of aerofoils have been used to efficiently control the forces they generate to attain flight control and aircraft trim. Change in the camber has generally been achieved through trailing edge flaps due to their simplicity and efficacy. However, a flap introduces a discontinuity that under certain flight conditions generates adverse pressure gradients and flow separation. This can cause a significant increase in drag thus lowering the aerodynamic efficiency and increasing the fuel consumption of the aircraft. Hence the analysis of aerodynamic performance of multi-element aerofoil is an important area of research.
An alternative approach to overcome this problem is to use a morphing aerofoil, which introduces a change in camber in a continuous fashion. The idea of a morphing aircraft that changes the wing shape or geometry is nothing new [Reference Weisshaar1]. It dates back to the Wright brothers who were twisting the wing of their glider during the flight to achieve control [Reference Culick2]. However, the improvement in payload and cruise speed has made such technology more challenging to implement. It is only with the recent advances in smart materials and adaptive structures that the idea of using morphing aerofoilss in modern-day aircraft [Reference Burdette and Martins3] or UAVs [Reference Bagul, Rana, Jenkins and Könözsy4, Reference Whu, Shi and Ang5] has come back as a credible contender to improve aerodynamic performances. In the last few years, morphing technologies have been the focus of major research projects for large aircraft with the development of a wide variety of designs [Reference Concilio, Dimino, Lecce and Pecora6, Reference Barbarino, Bilgen, Ajaj, Friswell and Inman7]. For example, in the framework of the SARISTU project [Reference Woelcken and Papadopoulos8], started in 2010, a wing with three morphing devices including an adaptive trailing edge [Reference Concilio, Dimino and Pecora9] was developed. Around the same time, in a concurrent project carried out by NASA and Boeing, another morphing trailing edge was presented [Reference Nguyen, Lebofsky, Ting, Kaul, Chaparro and Urnes10]. These two designs, although different both morph the aerofoil by using complex active kinematic system networks, which are generally heavy and come with important maintenance needs. In order to mitigate these drawbacks, designs using compliance-based approaches have been proposed [Reference Kota, Hetrick, Osborn, Paul, Pendleton, Flick and Tilmann11]. One example of such an approach is the FishBAC design [Reference Woods, Fincham and Friswell12, Reference Woods, Bilgen and Friswell13] that was taken as a reference for this study.
The primary motivation of using morphing aerofoil is the potential gain in aerodynamic performance it could offer, therefore, aerodynamic analysis is of crucial importance to motivate the use of this technology. Various numerical methods have been used in the literature to asses the aerodynamic performance of morphing aerofoil when considering subsonic flight conditions [Reference Woods, Fincham and Friswell12, Reference Hui, Zhang and Chen14]. Gabor et al. [Reference Sugar Gabor, Koreanschi, Botez, Mamou and Mebarki15] conducted experimental and numerical testing on a morphing wing with flexible top surface and controllable actuated ailerons. In their investigations, the authors optimised the performance of the wing for laminar flow region for Mach number up to 0.2 however they could not extend the Mach number range due to several constraints. The research considering morphing aerofoils under transonic flight condition (
![]() $M \approx 0.8$
) with high Reynolds number (
$M \approx 0.8$
) with high Reynolds number (
![]() $Re > 10^{6}$
) are a lot less frequent, especially when considering CFD methods. Some recent papers have however been dealing with the subject. Niu et al. [Reference Niu, Zhang, Chen and Zhang16], did use CFD for assessing the aerodynamic performance of aerofoils under transonic conditions, but only when considering low deflection angles and a constant start of the morphing part at 0.7
$Re > 10^{6}$
) are a lot less frequent, especially when considering CFD methods. Some recent papers have however been dealing with the subject. Niu et al. [Reference Niu, Zhang, Chen and Zhang16], did use CFD for assessing the aerodynamic performance of aerofoils under transonic conditions, but only when considering low deflection angles and a constant start of the morphing part at 0.7
![]() $x/c$
. Dumont [Reference Dumont17] used CFD for carrying out an aerodynamic shape optimisation for a morphing wing at a Mach number of 0.75. By changing the deflection of the trailing edge and the angle-of-attack an increase of the lift-to-drag ratio of
$x/c$
. Dumont [Reference Dumont17] used CFD for carrying out an aerodynamic shape optimisation for a morphing wing at a Mach number of 0.75. By changing the deflection of the trailing edge and the angle-of-attack an increase of the lift-to-drag ratio of
![]() $+2.6\%$
was found for
$+2.6\%$
was found for
![]() $C_l=0.52$
. The potential benefit of using morphing technologies in the supersonic regime has also been recently investigated using CFD. Dai et al. [Reference Dai, Yan, Huang, Zhen, Wang and Liu18] designed and performed an aerodynamic performance analysis of a variable sweep wing morphing wave-rider at a Mach number up to 8. They concluded that besides the effects of shock waves and wing down-wash these wave riders improve both low-and high-speed aerodynamics.
$C_l=0.52$
. The potential benefit of using morphing technologies in the supersonic regime has also been recently investigated using CFD. Dai et al. [Reference Dai, Yan, Huang, Zhen, Wang and Liu18] designed and performed an aerodynamic performance analysis of a variable sweep wing morphing wave-rider at a Mach number up to 8. They concluded that besides the effects of shock waves and wing down-wash these wave riders improve both low-and high-speed aerodynamics.
Current research is part of an effort to design, develop and test a concept of morphing aerofoil with a compliant trailing edge using a zero Poisson’s ratio skin presented in Zadeh et al. [Reference Zadeh, Dayyani and Yasaee19]. The morphing aerofoil will be considered under flow at a Mach number of
![]() $0.8$
and a Reynolds number of
$0.8$
and a Reynolds number of
![]() $3 \times 10^6$
for various deflections and start of the morphing part in order to find a set of parameters maximising the lift-to-drag ratio. The NACA0012 aerofoil will be used as a baseline aerofoil. In addition to the aerodynamic performance, shock location analysis is also essential. Under transonic flight conditions, a shock wave appears, which may cause structural damage to the morphing skin material. It is, therefore, preferable for the morphing part to be behind the shock region, which will be verified for every configuration in this study. In this work, a most favourable morphing aerofoil design among the run cases will be proposed based upon the aerodynamics performance, which (in future) may contribute to the experimental research into structural integrity of the design and impact of aeroelasticity.
$3 \times 10^6$
for various deflections and start of the morphing part in order to find a set of parameters maximising the lift-to-drag ratio. The NACA0012 aerofoil will be used as a baseline aerofoil. In addition to the aerodynamic performance, shock location analysis is also essential. Under transonic flight conditions, a shock wave appears, which may cause structural damage to the morphing skin material. It is, therefore, preferable for the morphing part to be behind the shock region, which will be verified for every configuration in this study. In this work, a most favourable morphing aerofoil design among the run cases will be proposed based upon the aerodynamics performance, which (in future) may contribute to the experimental research into structural integrity of the design and impact of aeroelasticity.
The design of a new morphing aerofoil concept entails a broader spectrum of factors to be considered. For instance, the presence of aeroelastic phenomena such as divergence and flutter plays a key role in the integrity of the aerofoil structure as it can lead to the failure of the wing structure. In the benchmark of morphing aerofoils for incompressible flows, a few studies have been carried out to determine the critical velocity and frequency at which flutter occurs as well as the divergence velocity. The first methods that have been used for static and dynamic aeroelasticity are found in Bisplinghoff et al. [Reference Bisplinghoff, Ashley and Halfman20] in which two degrees-of-freedom (DoF) analytical models are presented to analyze divergence and flutter of a 2D aerofoil. However, this model considered only the change in plunge and pitch. On the other hand, Murua et al. [Reference Murua, Palacios and Peiró21] proposed a three DoF model, in which the change of camber is considered, to study the influence of flutter in a 2D aerofoil. The results demonstrated that the camber mode can lead to linear flutter. Berci et al. [Reference Berci, Gaskell, Hewson and Toporov22] introduced model to study the influence of flutter and divergence solving the aeroelastic equations of motion by means of Ritz’s method in the fashion of Mass-Damper-Spring (MDS) system. This semi-analytical model also considered the effect of low camber deformations. The results of this analysis demonstrated that the camber deformation contributes to the increase of the aerodynamic loads. Although the previous aeroelastic analysis using the proposed model are essential as a first estimation of the aeroelastic effects in the morphing aerofoil design, the aerodynamic performance analysis can be considered as the first step in the design process by making the rigid-body assumption. This assumption seems reasonable for the authors, as the main purpose of current study is to obtain a preliminary design based on the behaviour of the flow field around the aerofoil in which aeroelastic phenomena can be neglected. This approach is valid to asses the flow field and obtain the aerodynamic coefficients of the lifting devices. Moreover, this assumption can be found in the works of Zhou et al. [Reference Zhou, Zhu, Main and Wang23], Woods et al. [Reference Woods, Fincham and Friswell12] and Huntley et al. [Reference Huntley, Woods and Allen24], among other authors whose focus is also on the analysis of the aerodynamic performance to establish a preliminary design of the morphing aerofoil.
The aerodynamics of aerofoils has been extensively developed since the beginning of the last century. These developments, such as the Potential Theory for thin aerofoils or the Lifting-line theory for wings [Reference Gordillo Arias de Saavedra and Riboux Acher25] allow us to understand how the flow around aerofoil devices behave. Furthermore, the performance of a single element aerofoil is limited by its design characteristics and cannot be improved since it is a rigid structure. On the other hand, it is known that the contribution of lift generation is achieved by the camber of the aerofoil according to Potential Theory. That is the reason why high-lift devices were developed, as they allow to change the camber of an aerofoil as well as increasing the reference area resulting in an increase in the lift-coefficient. However, these devices introduce additional drag penalties and an increase in noise due to the slot gap between devices as suggested by Refs [Reference Nguyen26, Reference Nguyen, Precup, Livne, Urnes, Dickey, Nelson, Chiew, Rodriguez, Ting and Lebofsky27]. As an alternative, morphing aerofoils offer a solution that reduces these problems by using a morphing part whose camber can be changed actively in a smooth fashion. Two main factors can be accounted for when considering the design of morphing aerofoils: deflections and starting morphing position (discussed below). It is worth noting that other factors, such as the thickness of the aerofoil or the shape of the deflection, also have an impact on the performance of the morphing aerofoil. As discussed by Huntley et al. [Reference Huntley, Woods and Allen24] they are however of less significance.
1.1 Deflections effects
Extensive research on the deflection effect has been carried out in order to understand the behaviour of the flow when the morphing part is deflected, and thus for a wide range of different methods. Panel methods (XFOIL) have been used by Refs [Reference Fincham and Friswell28, Reference Lafountain, Cohen and Abdallah29]. This approach permits to carry out an extensive number of simulations and is therefore really helpful for optimisation. To get results with stronger order of accuracy, CFD methods have also been used by Ref. [Reference Woods, Fincham and Friswell12, Reference Huntley, Woods and Allen24] and compared to panel methods with relatively good agreement for the Mach number considered. Experimental investigations have also been carried out by Refs [Reference Woods, Bilgen and Friswell13, Reference Kamliya Jawahar, Ai and Azarpeyvand30–Reference Yokozeki, Sugiura and Hirano32]. The results obtained by the above-mentioned authors show an increase in the lift as the deflection of the morphing part is increased. This is mainly achieved by the camber change in the morphing aerofoil showing the same flap-effect as when high-lift devices are used. As a result, the
![]() $C_{lmax}$
value is increased and the zero-lift angle is decreased. Furthermore, the stall angle decreases due to a steeper change in the camber of the aerofoil, which causes an earlier detachment of the boundary layer. Low-fidelity results, such as the one from Woods et al. [Reference Woods, Fincham and Friswell12] or Huntley et al. [Reference Huntley, Woods and Allen24] show good agreement when predicting the lift curve when compared to higher fidelity CFD results. Nevertheless, an under-prediction [Reference Woods, Fincham and Friswell12] or at the contrary an over-prediction [Reference Huntley, Woods and Allen24] of the stall angle was observed when comparing the results with the CFD data.
$C_{lmax}$
value is increased and the zero-lift angle is decreased. Furthermore, the stall angle decreases due to a steeper change in the camber of the aerofoil, which causes an earlier detachment of the boundary layer. Low-fidelity results, such as the one from Woods et al. [Reference Woods, Fincham and Friswell12] or Huntley et al. [Reference Huntley, Woods and Allen24] show good agreement when predicting the lift curve when compared to higher fidelity CFD results. Nevertheless, an under-prediction [Reference Woods, Fincham and Friswell12] or at the contrary an over-prediction [Reference Huntley, Woods and Allen24] of the stall angle was observed when comparing the results with the CFD data.
Focusing on the drag coefficient results, it can be seen that an increase in the deflection causes an increase in drag. This is mainly due to the flow phenomena occurring in the slot gap, which is a source of drag and noise, as earlier suggested. This increase in drag appears to be overpredicted by XFOIL when compared to CFD results, especially when considering high angles of attack. According to Woods et al. [Reference Woods, Fincham and Friswell12], this overprediction is mainly caused by the boundary layer model used by XFOIL, which results in boundary layer detachment earlier than expected, Thus, this effect is linked to the earlier stall of the aerofoil.
Furthermore, Refs [Reference Woods, Dayyani and Friswell33, Reference Woods and Friswell34] investigated the performance of the morphing concept through FSI simulations using XFOIL coupled with Euler-Bernoulli beam theory models. As observed, there has been a trend in using low-fidelity approaches in order to speed up the optimisation process, focusing only on obtaining the aerodynamics coefficients to measure the performance gain. This trend can be also seen in the work from Eguea et al. [Reference Eguea, Pereira Gouveia da Silva and Martini Catalano35] who uses a potential theory model coupled with a Boundary Layer Wing Fuselage (BLWF) subroutine to analyse the aerodynamic performance of the morphing device.
1.2 Starting morphing position effects
The effect of the start of the morphing location on the performance has also been extensively covered in the literature for both panel methods (XFOIL) and CFD methods [Reference Woods, Fincham and Friswell12, Reference Huntley, Woods and Allen24]. These studies have considered a wide range of start of the morphing location and show an increase in lift coefficient as the location get further downstream, this remains true for the angle-of-attack between
![]() $0^\circ$
and
$0^\circ$
and
![]() $15^\circ$
, no explanation could however be given as for why. When considering the drag, a small drag penalty was found when pushing the start of the morphing location toward the trailing edge of the aerofoil. This is due to the steeper curve of the deflection that is needed to keep the same maximum deflection with a later start of the morphing part. Generally moving the start of the morphing location downstream offered a slight increase in the aerodynamic performance. In addition to that having a small morphing part will increase the global stiffness of the wing as the flexibility needed to have a morphing aerofoil is needed on a smaller section of the wing. This is particularly important for transonic flow where a shock wave appears on the upper surface of the aerofoil and might damage the morphing skin.
$15^\circ$
, no explanation could however be given as for why. When considering the drag, a small drag penalty was found when pushing the start of the morphing location toward the trailing edge of the aerofoil. This is due to the steeper curve of the deflection that is needed to keep the same maximum deflection with a later start of the morphing part. Generally moving the start of the morphing location downstream offered a slight increase in the aerodynamic performance. In addition to that having a small morphing part will increase the global stiffness of the wing as the flexibility needed to have a morphing aerofoil is needed on a smaller section of the wing. This is particularly important for transonic flow where a shock wave appears on the upper surface of the aerofoil and might damage the morphing skin.
1.3 Morphing aerofoil against flapped aerofoil
The superior aerodynamic performance of morphing aerofoil when compared to more traditional discrete control surfaces has been well demonstrated. For example, Huntley et al. [Reference Huntley, Woods and Allen24] found, for a Mach number of 0.3, an increase of
![]() $5.7\%$
in the lift-to-drag ratio at
$5.7\%$
in the lift-to-drag ratio at
![]() $C_l=1.2$
, and
$C_l=1.2$
, and
![]() $107.1\%$
at
$107.1\%$
at
![]() $C_l=1.75$
. This is due to the increased drag that the slot gap between the main element and the flap produces as discussed in Refs [Reference Nguyen26, Reference Nguyen, Precup, Livne, Urnes, Dickey, Nelson, Chiew, Rodriguez, Ting and Lebofsky27]. For UAVs applications in particular, the potential of morphing technology has been thoroughly studied. In Bashir et al. [Reference Bashir, Longtin-Martel, Botez and Wong36], the potential of a morphing root aerofoil for a UAV was studied numerically. Following a thorough optimisation at different flight conditions, an improved aerodynamic performance was found when using a morphing trailing edge or a droop nose leading edge.
$C_l=1.75$
. This is due to the increased drag that the slot gap between the main element and the flap produces as discussed in Refs [Reference Nguyen26, Reference Nguyen, Precup, Livne, Urnes, Dickey, Nelson, Chiew, Rodriguez, Ting and Lebofsky27]. For UAVs applications in particular, the potential of morphing technology has been thoroughly studied. In Bashir et al. [Reference Bashir, Longtin-Martel, Botez and Wong36], the potential of a morphing root aerofoil for a UAV was studied numerically. Following a thorough optimisation at different flight conditions, an improved aerodynamic performance was found when using a morphing trailing edge or a droop nose leading edge.
As can be seen, extensive work has been carried out using both panel and CFD methods that have proven the potential of morphing technology in terms of increased performances. Most efficient geometries have also been investigated for a wide range of angles of attack and Mach numbers. However, the main effort has been put into understanding the aerodynamics at low Mach numbers (
![]() $M < 0.3$
). Only a few authors such as Lyu and Martins [Reference Lyu and Martins37] or Dumont [Reference Dumont17] have attempted to study this technology at transonic regime (
$M < 0.3$
). Only a few authors such as Lyu and Martins [Reference Lyu and Martins37] or Dumont [Reference Dumont17] have attempted to study this technology at transonic regime (
![]() $M = 0.8$
) using high fidelity methods. Nowadays commercial aircraft generally fly at a cruise speed of Mach 0.8, therefore extending the current work to take into consideration higher flow speed is of strategic importance. This project will attempt to achieve new knowledge on the physics of the interaction of the flow phenomena around a morphing aerofoil in the transonic regime, especially regarding the formation of shock waves around this device.
$M = 0.8$
) using high fidelity methods. Nowadays commercial aircraft generally fly at a cruise speed of Mach 0.8, therefore extending the current work to take into consideration higher flow speed is of strategic importance. This project will attempt to achieve new knowledge on the physics of the interaction of the flow phenomena around a morphing aerofoil in the transonic regime, especially regarding the formation of shock waves around this device.
2.0 Methodology
2.1 Numerical methods
A transonic outer flow is studied here, and should be considered as a compressible flow, therefore, the density-based solver has been employed in this research. The viscosity is calculated by the Sutherland’s law with three coefficients. The turbulent flow is simulated with the Reynolds Averaged Navier-Stokes (RANS) equations, which decomposes the instantaneous velocity into the sum of a mean and a fluctuating part [Reference Wilcox38]. After the time-averaging process, an additional term, Reynolds stress term
![]() $-\rho \overline{u'_i u'_j}$
, is introduced to the original Navier-Stokes equations and it contains six unknown components. Turbulence models are developed to close the system of equations, and the two equations Shear-Stress Transport (SST)
$-\rho \overline{u'_i u'_j}$
, is introduced to the original Navier-Stokes equations and it contains six unknown components. Turbulence models are developed to close the system of equations, and the two equations Shear-Stress Transport (SST)
![]() $k-\omega$
model is selected in this study. This model was introduced by Menter [Reference Menter39] and is one of the most popular RANS turbulence model for aerospace applications. The SST
$k-\omega$
model is selected in this study. This model was introduced by Menter [Reference Menter39] and is one of the most popular RANS turbulence model for aerospace applications. The SST
![]() $k-\omega$
model combines the standard
$k-\omega$
model combines the standard
![]() $k-\omega$
model and
$k-\omega$
model and
![]() $k-\epsilon$
model. In the inner region of the boundary layer the robust and accurate
$k-\epsilon$
model. In the inner region of the boundary layer the robust and accurate
![]() $k-\omega$
is used and in the free shear flow the
$k-\omega$
is used and in the free shear flow the
![]() $k-\epsilon$
is used to benefit from its free-stream independence. The Compressibility Effects for SST
$k-\epsilon$
is used to benefit from its free-stream independence. The Compressibility Effects for SST
![]() $k-\omega$
model is enabled because this can improve the prediction of the free shear flow at high Mach number. The standard SST
$k-\omega$
model is enabled because this can improve the prediction of the free shear flow at high Mach number. The standard SST
![]() $k-\omega$
is modified to take into account the transitional effect by using the Intermittency Transition Model introduced by Menter et al. [Reference Menter, Langtry, Likki and Suzen40].
$k-\omega$
is modified to take into account the transitional effect by using the Intermittency Transition Model introduced by Menter et al. [Reference Menter, Langtry, Likki and Suzen40].
The farfield flow conditions come from the wind tunnel experiments by Harris [Reference Harris41] who conducted the two-dimensional tests for the NACA0012 aerofoil in the Langley 8-foot transonic pressure tunnel. The data at
![]() $M=0.8$
for a Reynolds number of
$M=0.8$
for a Reynolds number of
![]() $3.0 \times 10^6$
is chosen to validate the numerical results of this study, similar flow conditions have been used by other authors to study the flow around an aerofoil in the transonic regime [Reference Sengupta, Bhole and Sreejith42, Reference Illi, Lutz and Krämer43]. The relation between the different flow variables is given in Equation (1). The turbulence intensity
$3.0 \times 10^6$
is chosen to validate the numerical results of this study, similar flow conditions have been used by other authors to study the flow around an aerofoil in the transonic regime [Reference Sengupta, Bhole and Sreejith42, Reference Illi, Lutz and Krämer43]. The relation between the different flow variables is given in Equation (1). The turbulence intensity
![]() $Tu_{far}$
is set to 1% and the viscosity ratio
$Tu_{far}$
is set to 1% and the viscosity ratio
![]() $\mu_t/\mu$
to 1.0.
$\mu_t/\mu$
to 1.0.
where
![]() $\gamma=1.4$
is the specific gas constant,
$\gamma=1.4$
is the specific gas constant,
![]() $c=1$
m is the chord length of NACA0012 aerofoil, a is the speed of sound and
$c=1$
m is the chord length of NACA0012 aerofoil, a is the speed of sound and
![]() $\mu$
is the kinematic viscosity. The aerofoil surface is set to be a no-slip viscous, adiabatic wall.
$\mu$
is the kinematic viscosity. The aerofoil surface is set to be a no-slip viscous, adiabatic wall.
The inviscid convective flux is calculated with the Roe-FDS scheme, which split the flux into different parts that contain the characteristic information travelling in particular directions. The second-order upwind scheme is selected as the spatial discretisation method and the Green-Gauss cell-based method for the computing of the gradient.
2.2 Geometry
In this section, the definition of the geometry chosen for this study will be discussed. Firstly, as previously mentioned, the main purpose of this research is to identify the physics of the flow around an aerofoil using morphing technology in the trailing edge. Namely, the focus will be on the interaction of the shock wave with the boundary layer as well as the change in deflection of the morphing part. Hence, a NACA0012 aerofoil has been chosen as reference geometry to implement the morphing technology. Although symmetrical aerofoils are not usually used for wing design since cambered aerofoils can outperform them, it was decided to choose this geometry for its simplicity, permitting to focus on the changes occurring in the flow field when the morphing part is deflected, isolating any possible effect that a cambered aerofoil could have. Furthermore, in a representative number of studies such as the FishBAC project [Reference Woods, Fincham and Friswell12, Reference Woods, Bilgen and Friswell13, Reference Zhou, Zhu, Main and Wang23, Reference Woods and Friswell44] or environmental flows [Reference Kamliya Jawahar, Ai and Azarpeyvand30], NACA0012 has been used as the baseline geometry and there is sufficient experimental and numerical data available for validation. On the other hand, no aeroelastic effects have been considered since it falls out of the scope of this project. Although, the authors of this research acknowledge that this is an aspect to focus on in the future as aeroelastic phenomena such as flutter and buffet may result in negative effects for the structural integrity of the wing. As regarded in the investigation of He et al. [Reference He, Guo and Li45] in which the author found that this technology can be of use to control the flutter generated by manipulating the harmful eddies and enhancing the beneficial ones by means of a vibrating TE (locking effect). Tô et al. [Reference Tô, Simiriotis, Marouf, Szubert, Asproulias, Zilli, Hoarau, Hunt and Braza46] focused their research on the effects of flutter when morphing technology is used in the TE concluding that the implementation of a morphing part can increase the transonic flutter speed up to 74.5%, as the shock wave can change of location and formation due to the change in the deflection of the morphing region. In order to achieve an optimal design that prevents these phenomena from occurring, several optimisations techniques have been used such as density-based approaches in conjunction with optimisation refinement techniques [Reference Zhang, Song, Yang, Cavalieri, De Gaspari and Ricci47], genetic algorithms [Reference Fincham and Friswell28, Reference El Maani, Elouardi, Radi and El Hami48–Reference Berci, Toropov, Hewson and Gaskell50] and adjoint-based methods [Reference Concilio, Dimino, Lecce and Pecora6] to enhance the performance of the aerofoils using morphing technology. However, these methods are time-consuming. For instance, genetic algorithms require a relatively high number of runs to establish the optimal operating points in the design. Whereas adjoint-based methods require several iterations of the algorithm to obtain a solution close to the optimal point. Furthermore, these methods are used as a tool to improve the characteristic, in this case, the aerodynamic performance, of a preliminary design. On the contrary, this study will be focused on the change in deflection and starting position of the morphing part to obtain a preliminary design of the morphing design using high-fidelity CFD simulations.
The morphing aerofoil will use the equations given in the work of Woods et al. [Reference Woods, Fincham and Friswell12]. The symmetric NACA0012 aerofoil is therefore used as a baseline, with a half thickness given by
where
![]() $\frac{x}{c}$
is the non-dimensional chord.
$\frac{x}{c}$
is the non-dimensional chord.
The trailing edge is morphed into a cubic curve, such curvature should be well adapted for describing morphing aerofoil based on a compliant approach. This is for example the case for the FishBAC concept [Reference Woods, Fincham and Friswell12, Reference Woods, Dayyani and Friswell33]. The camber line of the morphing part of the aerofoil is defined as follows
 \begin{equation} y_c=\left\{\begin{array}{l@{\quad}l} 0, & 0 \le \frac{x}{c} \le x_s \\[5pt] \dfrac{-w_{te}}{(1-x_s)^3}\left(\dfrac{x}{c}-x_s \right)^3 & x_s\le \dfrac{x}{c} \le 1 . \end{array}\right.\end{equation}
\begin{equation} y_c=\left\{\begin{array}{l@{\quad}l} 0, & 0 \le \frac{x}{c} \le x_s \\[5pt] \dfrac{-w_{te}}{(1-x_s)^3}\left(\dfrac{x}{c}-x_s \right)^3 & x_s\le \dfrac{x}{c} \le 1 . \end{array}\right.\end{equation}
This definition allows to directly control the start of the morphing part defined by
![]() $x_s$
, and the maximum deflection at the trailing edge when compared to the baseline NACA0012 defined by
$x_s$
, and the maximum deflection at the trailing edge when compared to the baseline NACA0012 defined by
![]() $w_{te}$
. The impact of these parameters on the geometry of the morphing aerofoil is summarised in Fig. 1.
$w_{te}$
. The impact of these parameters on the geometry of the morphing aerofoil is summarised in Fig. 1.

Figure 1. Morphing aerofoil geometry definition from Woods et al. [Reference Woods, Fincham and Friswell12].
The local slope of the morphing aerofoil is needed to define the final coordinates and is given by
Using Equations (2), (3) and (4) the points on the lower
![]() $(x_l,y_l)$
and upper
$(x_l,y_l)$
and upper
![]() $(x_u,y_u)$
surfaces of the morphing aerofoil are given by Equations (5), (6), (7) and (8).
$(x_u,y_u)$
surfaces of the morphing aerofoil are given by Equations (5), (6), (7) and (8).
To give an idea of what configurations have been tested, a few of them are presented in Fig. 2. A blunt trailing edge has been used, although due to its small size it is difficult to observe.

Figure 2. Example of geometries studied for the two extremes start of the morphing location and
![]() $w_{te}/c=[0.005,0.05,0.10]$
.
$w_{te}/c=[0.005,0.05,0.10]$
.
2.3 Grid generation
In this section, the meshing approach will be explained and is based on the strategy employed by Antoniadis et al. [Reference Antoniadis, Tsoutsanis and Drikakis51]. The different grids for the morphing aerofoil with its different deflections (
![]() $w_{te}$
) and starting morphing positions (
$w_{te}$
) and starting morphing positions (
![]() $x_{s}$
), were generated using a script based on the NACA0012 grid. They, therefore, have the same
$x_{s}$
), were generated using a script based on the NACA0012 grid. They, therefore, have the same
![]() $y+$
, expansion rate, number of points on aerofoil and domain extent.
$y+$
, expansion rate, number of points on aerofoil and domain extent.
In terms of grid topology, an unstructured C-grid type mesh has been chosen for this case consisting of quads and triangular cells. Several authors [Reference Woods, Fincham and Friswell12, Reference Huntley, Woods and Allen24, Reference Ai, Jawahar and Azarpeyvand31] use a structured grid. Opposite to this trend, it was decided to use the unstructured approach, since the mesh can be better adapted to more complex geometries as the morphing aerofoil with high deflections, for instance. Moreover, this approach allows clustering the grid points in the regions of interest where relevant phenomena such as turbulence occur. In Fig. 3, the dimension of the computational domain is presented as well as a zoom of the grid around the aerofoil. Further clustering was applied to the grid close to the aerofoil in a region extending 20 chord length with respect to the leading edge, and for a semicircle extending 1.5 chord length upstream. This refinement was applied in order to capture the turbulent features of the flow around the aerofoil and in its wake. The computational domain extends 100 chord lengths in the upstream and downstream directions. This size has been chosen as suggested by Refs [Reference Antoniadis, Tsoutsanis and Drikakis51, Reference Guo52] with the purpose of avoiding boundary interference with the flow.

Figure 3. Mesh boundary size (left) and grid point layout around NACA0012 aerofoil (right).
As observed in Table 1, three meshes have been generated with different refinement levels (coarse, medium and fine). The refinement criterion follows the guidelines suggested by Roache [Reference Roache53]. The refinement can be seen in Table 2.
Table 1. Refinement levels

Table 2. Number of grid points on the aerofoil and at the boundaries

Table 2 shows the number of grid points on the boundaries and aerofoil. Each region has been refined by multiplying the grid points by a factor of 1.5. According to Roache [Reference Roache53], it is suggested to refine the mesh by multiplying the grid points by a factor of 2. However, following that guideline will result in the coarser mesh unable to converge.
Furthermore, a wall-resolved strategy has been chosen setting the
![]() $y^{+}$
to be approximately 1 in order to model the turbulence in the viscous sublayer, as SST
$y^{+}$
to be approximately 1 in order to model the turbulence in the viscous sublayer, as SST
![]() $k-\omega$
turbulence model has been chosen. The refinement factor shows the same strategy as for the boundaries, and the same factor has been used to refine the boundary layer using a growth factor equal to 1.15.
$k-\omega$
turbulence model has been chosen. The refinement factor shows the same strategy as for the boundaries, and the same factor has been used to refine the boundary layer using a growth factor equal to 1.15.
2.4 Analysis parameters
Morphing aerofoil shapes with various start of the morphing locations, deflections and at various angles of attack were tested. The Mach and Reynolds numbers as well as the angles of attack found in Table 3 have been chosen according to the experimental data provided by Harris [Reference Harris41]. Furthermore, a relatively low deflection range has been used in order to avoid massive boundary layer detachment after the shock wave. Moreover, Tô et al. [Reference Tô, Simiriotis, Marouf, Szubert, Asproulias, Zilli, Hoarau, Hunt and Braza46] suggests that the designs of the morphing part should be able to slightly deflect in order to avoid aeroelastic instabilities such as buffeting. Finally, the range of morphing location has been chosen to be similar to the studies carried out by other authors (e.g. Huntley et al. [Reference Huntley, Woods and Allen24]). Therefore, these parameters will be used for validation (Table 4) purposes as well as the simulations performed on the morphing aerofoil (Tables 5 and 6).
Table 3. Flow and morphing aerofoil parameters

Table 4. Validation of drag and lift coefficients for the NACA0012 aerofoil at Mach number
![]() $0.8$
and Reynolds number
$0.8$
and Reynolds number
![]() $3 \times 10^{6}$
$3 \times 10^{6}$

Table 5. Optimal deflection, increase in lift and efficiency when compared to the baseline NACA0012

Table 6. Optimal deflections (
![]() $w_{te}/c$
) of all morphing setups at each AoA
$w_{te}/c$
) of all morphing setups at each AoA

3.0 Results and discussion
3.1 Validation
Before carrying out the analysis of the morphing aerofoil it is important to perform a grid convergence study and also validate the numerical results obtained against experimental data. In this report, the NACA0012 aerofoil is taken for that validation as it is the baseline of the morphing aerofoil. Similar to other simulations, a flow at a Mach number of
![]() $0.8$
and a Reynolds number of
$0.8$
and a Reynolds number of
![]() $3\times10^6$
is considered.
$3\times10^6$
is considered.
The Grid Convergence Index (GCI) methodology presented by Roache [Reference Roache53] was applied to the three NACA0012 grids presented in Section 2.3 for the aerodynamic coefficients
![]() $C_l$
and
$C_l$
and
![]() $C_d$
, at
$C_d$
, at
![]() $\alpha=2.94^{\circ}$
. This methodology permits to estimate the discretisation error by performing the simulation on a succession of further refined grids and calculating the GCI between two grids for a chosen quantity f. The definition of the GCI between a coarse grid and a fine grid is given as
$\alpha=2.94^{\circ}$
. This methodology permits to estimate the discretisation error by performing the simulation on a succession of further refined grids and calculating the GCI between two grids for a chosen quantity f. The definition of the GCI between a coarse grid and a fine grid is given as
r is the grid refinement ratio, z is the order of convergence and
![]() $F_s$
is a security factor, generally taken as 1.25 when considering 3 grids as is the case here. In this study, the GCIs of
$F_s$
is a security factor, generally taken as 1.25 when considering 3 grids as is the case here. In this study, the GCIs of
![]() $C_l$
and
$C_l$
and
![]() $C_d$
for the fine and medium grids are 0.09% and 1.81% respectively, against 14.3% and 33.0% between the medium and coarse. The high decrease in the GCIs indicates that further refinement will only slightly improve the results. Furthermore, the GCIs between fine and medium grids are really small indicating that the results are close to the asymptotic values. In addition to that in Fig. 4 it can be seen that the pressure distribution is nearly the same for the medium and fine grid. If from these results the medium grid seems to be the best compromise between accuracy and computational cost, the fine grid was selected to continue the following validation and morphing aerofoil analysis. This choice was motivated by the known requirement of highly refined grids for accurately capturing shock waves.
$C_d$
for the fine and medium grids are 0.09% and 1.81% respectively, against 14.3% and 33.0% between the medium and coarse. The high decrease in the GCIs indicates that further refinement will only slightly improve the results. Furthermore, the GCIs between fine and medium grids are really small indicating that the results are close to the asymptotic values. In addition to that in Fig. 4 it can be seen that the pressure distribution is nearly the same for the medium and fine grid. If from these results the medium grid seems to be the best compromise between accuracy and computational cost, the fine grid was selected to continue the following validation and morphing aerofoil analysis. This choice was motivated by the known requirement of highly refined grids for accurately capturing shock waves.

Figure 4.
![]() $C_p$
comparison between the three grids.
$C_p$
comparison between the three grids.
Extensive experimental data is available for the NACA0012. In this paper, the results from Harris [Reference Harris41] will be considered. In fact Harris [Reference Harris41] covers the flow condition considered in this study and was advised as the most accurate work when considering wind tunnel results for NACA0012 by Mccroskey [Reference Mccroskey54].
Table 4 presents the comparison of the lift and drag coefficients for various angles of attack between the experimental results of Harris [Reference Harris41] and the numerical ones. It can be noted that the values of AoA were corrected using the linear method for simulating wind-tunnel-wall interference given by Harris. As can be seen, good agreement is found between the experimental and numerical results. It can be noted that the lift coefficient was more accurately predicted than the drag coefficient. The discrepancies in results between experiment and CFD is due to various parameters such as the operating conditions, the choice of turbulence model, errors introduced at the digitisation of the wind tunnel data, etc. It can be observed that the error from
![]() $C_d$
and
$C_d$
and
![]() $C_l$
tend to decrease as the angle-of-attack increases. This trend is likely due to the presence of a secondary shock on the lower part of the aerofoil that is found in the simulation at higher AoAs than what is found experimentally. Furthermore, the use of
$C_l$
tend to decrease as the angle-of-attack increases. This trend is likely due to the presence of a secondary shock on the lower part of the aerofoil that is found in the simulation at higher AoAs than what is found experimentally. Furthermore, the use of
![]() $k-\omega$
SST turbulence model which was designed for flow with high curvature might be another factor explaining that decreasing error. In addition to the comparison to experimental data, the result for an angle-of-attack of
$k-\omega$
SST turbulence model which was designed for flow with high curvature might be another factor explaining that decreasing error. In addition to the comparison to experimental data, the result for an angle-of-attack of
![]() $0^\circ$
is added at it is known that for a symmetric aerofoil, as is NACA0012, the lift coefficient should be 0. The lift coefficient found is indeed really close to that value.
$0^\circ$
is added at it is known that for a symmetric aerofoil, as is NACA0012, the lift coefficient should be 0. The lift coefficient found is indeed really close to that value.
The distribution of the pressure coefficient
![]() $C_p$
around the aerofoil is another important indicator to see if the flow is correctly captured. Figure 5 gives the comparison of the pressure distribution obtained numerically and experimentally. It is important to note that the correction for wall-interference, is only a correction on the forces and the pressure distribution is actually not impacted by wall-interference. Therefore the results are given for uncorrected angles of attack. It can be seen that the experimental and numerical contours are generally in good agreement. The over-prediction of the shock location on the upper surface of the aerofoil by the CFD can however be noted. In addition to that, it appears that the secondary shock wave on the lower surface of the aerofoil that appears for low angle-of-attack starts to appear at a slightly higher angle for the CFD result than the experimental one. The over-prediction of shock location shouldn’t be too problematic for our discussion as the worry is on avoiding the shock wave to be on the morphing part. The over-prediction will therefore function as a security factor. Since the aerodynamic coefficients are well predicted and the main flow characteristics are captured, this set up was deemed accurate enough to carry out the aerodynamic analysis of the morphing aerofoil.
$C_p$
around the aerofoil is another important indicator to see if the flow is correctly captured. Figure 5 gives the comparison of the pressure distribution obtained numerically and experimentally. It is important to note that the correction for wall-interference, is only a correction on the forces and the pressure distribution is actually not impacted by wall-interference. Therefore the results are given for uncorrected angles of attack. It can be seen that the experimental and numerical contours are generally in good agreement. The over-prediction of the shock location on the upper surface of the aerofoil by the CFD can however be noted. In addition to that, it appears that the secondary shock wave on the lower surface of the aerofoil that appears for low angle-of-attack starts to appear at a slightly higher angle for the CFD result than the experimental one. The over-prediction of shock location shouldn’t be too problematic for our discussion as the worry is on avoiding the shock wave to be on the morphing part. The over-prediction will therefore function as a security factor. Since the aerodynamic coefficients are well predicted and the main flow characteristics are captured, this set up was deemed accurate enough to carry out the aerodynamic analysis of the morphing aerofoil.

Figure 5. Comparison of the numerical and experimental [Reference Harris41] pressure distribution for various angles of attack.
3.2 Start of the morphing location and deflection effects
The purpose of this section is to describe the behaviour of the flow at
![]() $M = 0.8$
around a morphing aerofoil with a morphing part starting between 65% and 80% of the chord length, and a deflection of the morphing part within the range from 0.5% to 10% of the chord length. The aerofoil will be considered as a rigid body and no aeroelastic phenomena will therefore be taken into account, similarly, the effect of changing the order of the curvature of the morphing part will not be studied. These subjects will be left for future studies. Firstly the velocity field around the aerofoil will be analysed in order to understand the nature of the flow around the device. The pressure distribution will then be studied and help to further understand the flow phenomena around the aerofoil, in particular the shock wave formation. Then the aerodynamic coefficients will be analysed in order to assess the performance of the morphing aerofoil with respect to the Baseline NACA0012 aerofoil. The shock wave location will also be studied due to concerns about its impact on the zero Poisson’s ratio meta-material skin.
$M = 0.8$
around a morphing aerofoil with a morphing part starting between 65% and 80% of the chord length, and a deflection of the morphing part within the range from 0.5% to 10% of the chord length. The aerofoil will be considered as a rigid body and no aeroelastic phenomena will therefore be taken into account, similarly, the effect of changing the order of the curvature of the morphing part will not be studied. These subjects will be left for future studies. Firstly the velocity field around the aerofoil will be analysed in order to understand the nature of the flow around the device. The pressure distribution will then be studied and help to further understand the flow phenomena around the aerofoil, in particular the shock wave formation. Then the aerodynamic coefficients will be analysed in order to assess the performance of the morphing aerofoil with respect to the Baseline NACA0012 aerofoil. The shock wave location will also be studied due to concerns about its impact on the zero Poisson’s ratio meta-material skin.
3.2.1 Velocity field
In this section, the velocity field will be evaluated in order to understand the nature of the shock wave and also the development of the wake. For this purpose, Fig. 6 shows the Mach contours for every deflection at an angle-of-attack equal to 0 degrees and for
![]() $x_s$
=0.8. This is done with the objective of showing the effects of the deflection.
$x_s$
=0.8. This is done with the objective of showing the effects of the deflection.

Figure 6. Velocity fields for different deflections at
![]() $x_s=0.80$
,
$x_s=0.80$
,
![]() $\alpha=0^\circ$
$\alpha=0^\circ$
![]() $Re=3\times10^6$
and
$Re=3\times10^6$
and
![]() $Ma=0.8$
.
$Ma=0.8$
.
A strong shock wave can be observed on the upper surface of the aerofoil. The location of that shock moves further downstream as the deflection
![]() $x_s$
increases. This shock affects the attachment of the boundary layer as it can be seen that the thickness of such region grows after the shock wave. This is caused by the instabilities generated from the strong gradient in the shock. The trend shows that an increase in the deflection causes the boundary layer to detach earlier and is the main reason why the maximum efficiencies are found at small deflection values as can be observed in Table 6. Furthermore, the boundary layer on the lower surface starts to detach near the trailing edge region when the morphing part is deflected more than 5% of chord length. This is due to an adverse pressure gradient generated in that region.
$x_s$
increases. This shock affects the attachment of the boundary layer as it can be seen that the thickness of such region grows after the shock wave. This is caused by the instabilities generated from the strong gradient in the shock. The trend shows that an increase in the deflection causes the boundary layer to detach earlier and is the main reason why the maximum efficiencies are found at small deflection values as can be observed in Table 6. Furthermore, the boundary layer on the lower surface starts to detach near the trailing edge region when the morphing part is deflected more than 5% of chord length. This is due to an adverse pressure gradient generated in that region.
Looking at the development of the shock wave on the upper surface of the aerofoil, Fig. 6 shows that the shock wave becomes more oblique as the deflection of the morphing part increase. This increasing shock obliquity is due to geometrical reasons. This means that the shock wave adapts in order to deflect the flow in the direction of the deflection.
Furthermore, a secondary shock wave can be observed on the lower surface of the aerofoil for small and intermediate deflections (0.5% to 2.5%). This shock can be observed to lose its strength as the deflection percentage increases. At a deflection of 2% this secondary shock splits into two weak shock waves before vanishing for higher deflection values. This phenomenon is related to the increase of the curvature with the deflection, hence increasing the turning of the flow, which makes the suction area on the upper surface increase and causes the flow acceleration to be lower on the bottom surface. Therefore achieving velocity below the critical Mach number.
The trends explained for a morphing aerofoil at zero angle-of-attack can also be seen when increasing the AoA, showing subtle differences when this parameter is varied. Namely, it can be seen that the shock wave moves further away from the morphing part and the secondary shock wave vanishes due to the lower acceleration experienced on the lower surface when the AoA increases.
3.2.2 Pressure distribution
In the previous section, a thorough analysis of the velocity contours around the aerofoil has been given. In this section, the pressure field around the aerofoil at an AoA equal to 0 degrees and for
![]() $x_s=0.8$
will be given in order to better understand the effects caused by the deflection of the morphing part. The pressure distribution (
$x_s=0.8$
will be given in order to better understand the effects caused by the deflection of the morphing part. The pressure distribution (
![]() $C_{p}$
) along the morphing aerofoil chord length will then be analysed in order to further describe the flow phenomena occurring around this device for every angle-of-attack tested.
$C_{p}$
) along the morphing aerofoil chord length will then be analysed in order to further describe the flow phenomena occurring around this device for every angle-of-attack tested.
Focusing further on the effect caused only by the deflection of the morphing aerofoil, the pressure field around the morphing aerofoil at an angle-of-attack of zero degrees is presented in Fig. 7. Observing the contours the same primary and secondary shock waves observed in Fig. 6 can be seen. Looking at the region near the lower surface of the trailing edge, it can be seen that as deflection increases, a positive pressure gradient is generated in the morphing part of the aerofoil contributing to the generation of the lift. This phenomenon can be described as the secondary source of lift generation of the morphing aerofoil apart from the great suction peak formed on the upper surface. This pressure increase can be also observed in the
![]() $C_{p}$
distribution for the whole range of AoAs in Fig. 8 as well as in the pressure field contours for the other values of AoA. As was already discussed in Section 3.2.1, the fact that the shock wave becomes more oblique as the deflection of the morphing part increases can be observed. As the shock wave becomes oblique, its strength is also reduced. This can be determined by the examination of the pressure difference across the shock wave which is reducing with the deflection, showing that the shock is weakening. This trend can be well observed in Fig. 8 for the whole range of AoA, except at zero degrees in which the shock wave strength seems to increase when the TE is deflected up to 1% of the chord length.
$C_{p}$
distribution for the whole range of AoAs in Fig. 8 as well as in the pressure field contours for the other values of AoA. As was already discussed in Section 3.2.1, the fact that the shock wave becomes more oblique as the deflection of the morphing part increases can be observed. As the shock wave becomes oblique, its strength is also reduced. This can be determined by the examination of the pressure difference across the shock wave which is reducing with the deflection, showing that the shock is weakening. This trend can be well observed in Fig. 8 for the whole range of AoA, except at zero degrees in which the shock wave strength seems to increase when the TE is deflected up to 1% of the chord length.

Figure 7. Pressure fields for different deflections at
![]() $x_s=0.8$
,
$x_s=0.8$
,
![]() $\alpha=0^\circ$
,
$\alpha=0^\circ$
,
![]() $Re=3\times10^6$
and
$Re=3\times10^6$
and
![]() $Ma=0.8$
.
$Ma=0.8$
.

Figure 8.
![]() $C_p$
distributions for different deflections and angles of attack at
$C_p$
distributions for different deflections and angles of attack at
![]() $x_s=0.8$
,
$x_s=0.8$
,
![]() $Re=3\times10^6$
and
$Re=3\times10^6$
and
![]() $Ma=0.8$
.
$Ma=0.8$
.
The impact of the angle-of-attack on the flow with respect to the deflection is well illustrated by the Fig. 8 that shows the
![]() $C_{p}$
distribution at angles of attack ranging from 0 degrees to 3.86 degrees. Three categories can be observed in the
$C_{p}$
distribution at angles of attack ranging from 0 degrees to 3.86 degrees. Three categories can be observed in the
![]() $C_{p}$
distribution: low deflections (black), intermediate deflections (red) and high deflections (blue). Firstly, the results for the whole range of AoA show that the difference in pressure between the upper and lower surface increase when the morphing part is further deflected. This is translated in greater lift generation which can be clearly observed when comparing the baseline NACA0012 aerofoil and the morphing aerofoil. The baseline geometry does not generate lift at an AoA equal to zero degrees as is expected from a symmetrical aerofoil, whereas the morphing aerofoil generates a substantial lift. This higher lift for the morphing aerofoil can also be observed for AoAs greater than zero degrees. It can therefore be stated that the change in camber causes a change in the pressure field and generates additional lift with respect to the baseline case as a result of morphing the TE. Secondly, a suction peak can be observed on the upper surface of the morphing aerofoil which can extend from 0.3 to 0.7 chord length, approximately. This suction is caused by a favourable pressure gradient generated at the leading edge. Furthermore, the strength of the favourable pressure gradient is observed to be greater when increasing the AoA and deflection. After the suction peak region, a sudden increase (pressure discontinuity) in the pressure can be observed in the
$C_{p}$
distribution: low deflections (black), intermediate deflections (red) and high deflections (blue). Firstly, the results for the whole range of AoA show that the difference in pressure between the upper and lower surface increase when the morphing part is further deflected. This is translated in greater lift generation which can be clearly observed when comparing the baseline NACA0012 aerofoil and the morphing aerofoil. The baseline geometry does not generate lift at an AoA equal to zero degrees as is expected from a symmetrical aerofoil, whereas the morphing aerofoil generates a substantial lift. This higher lift for the morphing aerofoil can also be observed for AoAs greater than zero degrees. It can therefore be stated that the change in camber causes a change in the pressure field and generates additional lift with respect to the baseline case as a result of morphing the TE. Secondly, a suction peak can be observed on the upper surface of the morphing aerofoil which can extend from 0.3 to 0.7 chord length, approximately. This suction is caused by a favourable pressure gradient generated at the leading edge. Furthermore, the strength of the favourable pressure gradient is observed to be greater when increasing the AoA and deflection. After the suction peak region, a sudden increase (pressure discontinuity) in the pressure can be observed in the
![]() $C_{p}$
distribution which corresponds to the formation of the shock wave on the upper surface and appears in all cases. Also, it has been observed that the increase of the pressure gradient due to the increment of AoAs causes the shock wave to occur earlier. This is due to the acceleration transmitted to the flow by means of the favourable pressure gradient at the leading edge. On the other hand, as was already observed for the velocity, an increase in deflection tends to make the shock wave travel further downstream closer to the morphing part. This phenomenon is due to the shock wave adapting to the deflection, affecting also its angle of incidence. Furthermore, Fig. 8 shows that the secondary shock on the lower surface of the aerofoil discussed in Section 3.2.1 only appears at an AoA of 0. This shock is due to the small curvature of the morphing aerofoil for a low deflection and an AoA of 0 which causes the flow to accelerate almost symmetrically. This can be observed in the oscillations produced in the
$C_{p}$
distribution which corresponds to the formation of the shock wave on the upper surface and appears in all cases. Also, it has been observed that the increase of the pressure gradient due to the increment of AoAs causes the shock wave to occur earlier. This is due to the acceleration transmitted to the flow by means of the favourable pressure gradient at the leading edge. On the other hand, as was already observed for the velocity, an increase in deflection tends to make the shock wave travel further downstream closer to the morphing part. This phenomenon is due to the shock wave adapting to the deflection, affecting also its angle of incidence. Furthermore, Fig. 8 shows that the secondary shock on the lower surface of the aerofoil discussed in Section 3.2.1 only appears at an AoA of 0. This shock is due to the small curvature of the morphing aerofoil for a low deflection and an AoA of 0 which causes the flow to accelerate almost symmetrically. This can be observed in the oscillations produced in the
![]() $C_{p}$
distribution as well as in the pressure field, shown in Fig. 7.
$C_{p}$
distribution as well as in the pressure field, shown in Fig. 7.
Therefore, it has been observed that the location of the shock waves varies depending on the AoA and the deflection. Thus, the shock wave shifts away from the morphing part as the AoA is increased. The opposite effect is found, when the deflection of the morphing element is increased.
3.2.3 Aerodynamic coefficients
In Figs 9 and 10, the results of the aerodynamic coefficients with respect to the deflections for different AoAs are shown.

Figure 9.
![]() $C_{l}$
for different deflections, angles of attack and start of the morphing part at
$C_{l}$
for different deflections, angles of attack and start of the morphing part at
![]() $Re = 3\times10^{6}$
and
$Re = 3\times10^{6}$
and
![]() $M = 0.8$
.
$M = 0.8$
.

Figure 10.
![]() $C_{d}$
for different deflections, angles of attack and start of the morphing part at
$C_{d}$
for different deflections, angles of attack and start of the morphing part at
![]() $Re = 3\times10^{6}$
and
$Re = 3\times10^{6}$
and
![]() $M = 0.8$
.
$M = 0.8$
.
Focusing on the lift coefficient
![]() $C_{l}$
, it can be observed that it increases, as the deflection and angle-of-attack increase. This is coherent with the
$C_{l}$
, it can be observed that it increases, as the deflection and angle-of-attack increase. This is coherent with the
![]() $C_p$
distribution presented in Fig. 8 and is a similar trend that what was found in the subsonic regime, for example by Huntley et al. [Reference Huntley, Woods and Allen24]. Furthermore, the trend shows that the gain in lift is significant when changing the AoA from 0 degrees to 1.66 degrees. However, the gains in lift obtained when further increasing the AoA are less significant, this is particularly obvious when looking at higher deflections of the morphing part. This diminishing increase in
$C_p$
distribution presented in Fig. 8 and is a similar trend that what was found in the subsonic regime, for example by Huntley et al. [Reference Huntley, Woods and Allen24]. Furthermore, the trend shows that the gain in lift is significant when changing the AoA from 0 degrees to 1.66 degrees. However, the gains in lift obtained when further increasing the AoA are less significant, this is particularly obvious when looking at higher deflections of the morphing part. This diminishing increase in
![]() $C_l$
with the AoA was of course expected and has been extensively documented [Reference Harris41]. Fluctuations in
$C_l$
with the AoA was of course expected and has been extensively documented [Reference Harris41]. Fluctuations in
![]() $C_{l}$
can be observed at small deflections of the morphing part for any AoA, but in particular at
$C_{l}$
can be observed at small deflections of the morphing part for any AoA, but in particular at
![]() $\alpha=0$
. This is due to the interaction of the secondary shock wave located on the lower surface with the flow. In fact, this shock has a non-negligible impact on the lift, as can be seen in Fig. 8. However, it is greatly impacted by deflection, quickly disappearing with an increasing deflection. This secondary shock can therefore explain why the oscillations are only observed for small deflections. Furthermore, this secondary shock is the most important at an AoA of 0, explaining the bigger oscillations of
$\alpha=0$
. This is due to the interaction of the secondary shock wave located on the lower surface with the flow. In fact, this shock has a non-negligible impact on the lift, as can be seen in Fig. 8. However, it is greatly impacted by deflection, quickly disappearing with an increasing deflection. This secondary shock can therefore explain why the oscillations are only observed for small deflections. Furthermore, this secondary shock is the most important at an AoA of 0, explaining the bigger oscillations of
![]() $C_l$
observed for that particular angle-of-attack. Regarding the drag coefficient
$C_l$
observed for that particular angle-of-attack. Regarding the drag coefficient
![]() $C_{d}$
, a rise can be observed when increasing both deflection and AoA. This is due to the boundary layer detachment as it separates from the aerofoil as the camber of the aerofoil and angle-of-attack increase. The fluctuations of
$C_{d}$
, a rise can be observed when increasing both deflection and AoA. This is due to the boundary layer detachment as it separates from the aerofoil as the camber of the aerofoil and angle-of-attack increase. The fluctuations of
![]() $C_d$
at small deflections can be also observed as a result of the same effect caused by the secondary shock wave.
$C_d$
at small deflections can be also observed as a result of the same effect caused by the secondary shock wave.
Comparing the aerodynamic coefficients with the Baseline NACA0012 aerofoil, the results show that the morphing aerofoil is able to generate up to 125% more lift than the baseline case. As for the
![]() $C_{d}$
values, it is observed that there is more drag generation for the whole range of AoA and deflections compared to the baseline case. This is due to the instabilities caused by the shock wave located on the upper surface, which makes the boundary layer thickness grow, meaning that the flow becomes more turbulent within this region, and detaches from the aerofoil at higher angles of attack.
$C_{d}$
values, it is observed that there is more drag generation for the whole range of AoA and deflections compared to the baseline case. This is due to the instabilities caused by the shock wave located on the upper surface, which makes the boundary layer thickness grow, meaning that the flow becomes more turbulent within this region, and detaches from the aerofoil at higher angles of attack.
Looking at the
![]() $C_{l}/C_{d}$
ratio, Fig. 11 shows that the most efficient deflection setups are achieved with small deflections between 1.0% and 2.5% of the chord length. Then, the trend shows that after reaching the optimal point at each AoA, the efficiency of the morphing aerofoil decreases abruptly, meaning that the generation of drag increases faster than the lift generation. This is due to boundary layer detachment for higher AoA values and growth of the boundary layer thickness for the morphing aerofoil at zero degrees as a result of the instabilities caused by the shock wave. This can be seen in Fig. 6.
$C_{l}/C_{d}$
ratio, Fig. 11 shows that the most efficient deflection setups are achieved with small deflections between 1.0% and 2.5% of the chord length. Then, the trend shows that after reaching the optimal point at each AoA, the efficiency of the morphing aerofoil decreases abruptly, meaning that the generation of drag increases faster than the lift generation. This is due to boundary layer detachment for higher AoA values and growth of the boundary layer thickness for the morphing aerofoil at zero degrees as a result of the instabilities caused by the shock wave. This can be seen in Fig. 6.

Figure 11.
![]() $C_l/C_d$
for different deflections and angles of attack at
$C_l/C_d$
for different deflections and angles of attack at
![]() $Re=3\times10^6$
and
$Re=3\times10^6$
and
![]() $Ma=0.8$
.
$Ma=0.8$
.
As observed in Fig. 11, there are deflections for each AoA where the maximum lift-to-drag ratio is achieved. These can be defined as optimal deflections. Table 5 shows the optimal deflection for each angle-of-attack. As remarked before, the optimal deflections are between 1.0% and 2.5% of the chord length, as shown above. It can be seen that the highest increment in
![]() $C_{l}$
is equal to 0.5438 at zero angle-of-attack. This can also be seen in terms of
$C_{l}$
is equal to 0.5438 at zero angle-of-attack. This can also be seen in terms of
![]() $C_{l}/C_{d}$
with the highest increment also found at zero angle-of-attack. Such difference makes the morphing aerofoil at this angle the most efficient setup. However, the optimal deflections at the rest of AoA values achieve between 80% and 90% increase in the
$C_{l}/C_{d}$
with the highest increment also found at zero angle-of-attack. Such difference makes the morphing aerofoil at this angle the most efficient setup. However, the optimal deflections at the rest of AoA values achieve between 80% and 90% increase in the
![]() $C_{l}$
and between 11% and 19% increase in the
$C_{l}$
and between 11% and 19% increase in the
![]() $C_{l}/C_{d}$
.
$C_{l}/C_{d}$
.
After analyzing the aerodynamic coefficients, it can be seen that the variation in the deflections of the morphing aerofoil in the transonic regime causes the same effects on lift and drag as in the study from Huntley et al. [Reference Huntley, Woods and Allen24], who investigated the aerodynamic effects of the morphing aerofoil for moderate Reynolds and low Mach numbers in which they obtained a 25% increase in the lift-to-drag ratio.
3.2.4 Shock wave location
Unlike in the subsonic regime, the shock wave location is introduced in the aerodynamic analysis of the morphing aerofoil in transonic regime. In the present study the material used for the morphing section is different from the rest of the aerofoil. In fact, in order to obtain a continuous deflection using a compliant system, a zero Poisson’s ratio skin is used for the morphing part. This material has lower strength than the fixed part. Therefore, the location of the shock wave must be considered in order to ensure that it is not near the morphing part and causes damage to the zero Poisson’s ratio skin.
Observing Fig. 12, the shock wave location along the aerofoil chord length is represented. The fact that under some conditions the shock wave is near or over the morphing part can be seen and prove the importance of taking that parameter into consideration. It can be observed that when the angle-of-attack increases, the shock wave moves further upstream, away from the morphing part, as expected. The impact of the deflection on the shock wave location appears to be less obvious. Generally increasing the deflection appears to make the shock move downstream, but when considering high deflection for high AoAs the trend seems to be reversed. This movement downstream of the shock caused by an increase in deflection is especially obvious when considering an AoA of
![]() $0^{\circ}$
and the morphing configurations starting at 70% and 80% of the chord length, where there is a sudden change in the position of the shock wave, surpassing the threshold between the rigid and morphing region. This effect is caused by the adaptation of the shock wave with the geometry as was discussed in Section 3.2.1.
$0^{\circ}$
and the morphing configurations starting at 70% and 80% of the chord length, where there is a sudden change in the position of the shock wave, surpassing the threshold between the rigid and morphing region. This effect is caused by the adaptation of the shock wave with the geometry as was discussed in Section 3.2.1.

Figure 12. Shock wave location for different deflections and angles of attack,
![]() $Re= 3\times10^6$
and
$Re= 3\times10^6$
and
![]() $Ma= 0.8$
compared to the baseline NACA0012.
$Ma= 0.8$
compared to the baseline NACA0012.
Considering the potential risks that the shock wave near the morphing part can cause, the results show that there is nearly no potential skin damage within the range of AoA from 1.66 to 3.86 degrees for the whole range of deflections. When considering an AoA of
![]() $0^{\circ}$
it can be seen that the morphing configuration with
$0^{\circ}$
it can be seen that the morphing configuration with
![]() $x_s/c=0.65$
is unacceptable with a shock wave on the morphing part for nearly every deflection. The other
$x_s/c=0.65$
is unacceptable with a shock wave on the morphing part for nearly every deflection. The other
![]() $x_s$
considered are more promising, if for high deflections they do have shock wave close or on the morphing part, when considering that the optimal deflections are around 1%–2.5% they appear to be safe.
$x_s$
considered are more promising, if for high deflections they do have shock wave close or on the morphing part, when considering that the optimal deflections are around 1%–2.5% they appear to be safe.
3.3 Comparative analysis
Previously, the aerodynamic effects of the morphing aerofoil setups with a starting location for the morphing part ranging between 0.65 to 0.80 chord length and a deflection between 0 and 0.1 have been analysed. The results for all the configurations have shown that the morphing aerofoil at
![]() $M = 0.8$
and
$M = 0.8$
and
![]() $Re = 3 \times 10^{6}$
achieves an increase in lift similar to the trend found at low Mach numbers and moderate Reynolds numbers
$Re = 3 \times 10^{6}$
achieves an increase in lift similar to the trend found at low Mach numbers and moderate Reynolds numbers
![]() $(Re < 10^{6})$
, as shown in the previous studies, i.e. Huntley et al. [Reference Huntley, Woods and Allen24].
$(Re < 10^{6})$
, as shown in the previous studies, i.e. Huntley et al. [Reference Huntley, Woods and Allen24].
This section aims to compare the results for the optimal deflection of four morphing aerofoil setups, as the purpose of this study is to obtain the most efficient design that maximises lift generation and minimises drag. Needless to say, that an aircraft flight is divided into three stages: take-off, cruise and landing. For each phase of the flight, the aircraft will need a different setup to obtain the required lift. However, this is analysis is not in the scope of this study.
After analysing the optimal deflections, another important parameter discussed in the results analysis is the location of the shock wave. This parameter is important due to the potential risk of damage to the zero Poisson’s ratio skin if the shock wave is found on the morphing part of the aerofoil.
3.3.1 Optimal deflections
The optimal deflections have been determined in the previous sections. A summary of the results below in Table 6. It is observed that there is not a clear pattern in the optimal deflections and these are dependent on the geometry. However, the results show that small deflections are the most efficient points achieving the highest lift-to-drag ratio for each starting morphing position (
![]() $x_{s}/c$
). Table 6 alongside with Fig. 13 provides information of the optimal deflection at a certain angle-of-attack and its lift-to-drag (
$x_{s}/c$
). Table 6 alongside with Fig. 13 provides information of the optimal deflection at a certain angle-of-attack and its lift-to-drag (
![]() $C_{l}/C_{d}$
) ratio value. Considering these three parameters, the most efficient morphing aerofoil setup can be determined.
$C_{l}/C_{d}$
) ratio value. Considering these three parameters, the most efficient morphing aerofoil setup can be determined.

Figure 13. Lift-to-drag ratio of optimal deflections.
Focusing on the lift-to-drag ration (
![]() $C_{l}/C_{d}$
), the trend shows that the aerodynamic efficiency decreases if the angles of attack are increased for any starting morphing position (
$C_{l}/C_{d}$
), the trend shows that the aerodynamic efficiency decreases if the angles of attack are increased for any starting morphing position (
![]() $x_{s}/c$
). However, the aerofoils with morphing parts starting at 0.65 and 0.70 chord length experience more efficiency loss at 2.86 and 3.86 degrees than for aerofoils with a shorter morphing part. On the other hand, the optimal deflections at zero degrees achieve the highest
$x_{s}/c$
). However, the aerofoils with morphing parts starting at 0.65 and 0.70 chord length experience more efficiency loss at 2.86 and 3.86 degrees than for aerofoils with a shorter morphing part. On the other hand, the optimal deflections at zero degrees achieve the highest
![]() $C_{ l}/C_{d}$
values, becoming the most aerodynamic efficient angle. Namely, the morphing aerofoil with a starting morphing position
$C_{ l}/C_{d}$
values, becoming the most aerodynamic efficient angle. Namely, the morphing aerofoil with a starting morphing position
![]() $x_{s}/c = 0.80$
obtains
$x_{s}/c = 0.80$
obtains
![]() $C_{ l}/C_{d} = 17.23$
.
$C_{ l}/C_{d} = 17.23$
.
3.3.2 Shock wave location
The shock wave location must be considered in order to ensure the integrity of the morphing structure, as previously remarked. Looking at Fig. 14, the aerofoil with a morphing part starting at 0.8 ensures that the shock wave is located away from the morphing part for the whole range of AoAs. With this setup, the shock wave can be found at a minimum of 0.13 chord length away from the morphing part. On the contrary, other aerofoils with a starting morphing position at 0.65 chord length do not ensure the structural integrity of the morphing part, since the shock wave can be found within this region. A scattered trend of the curves presented can be observed which is due to the optimal deflection changing for different angles of attack or
![]() $x_s$
. The deflection has indeed been shown to play an important role in the shock wave location.
$x_s$
. The deflection has indeed been shown to play an important role in the shock wave location.

Figure 14. Shock wave location of optimal deflections.
Having considered the lift-to-drag ration (
![]() $C_{ l}/C_{d}$
) and the shock wave location, it has been determined that the morphing aerofoil with a morphing part starting (
$C_{ l}/C_{d}$
) and the shock wave location, it has been determined that the morphing aerofoil with a morphing part starting (
![]() $x_{s}/c$
) at 0.8 chord length, a deflection (
$x_{s}/c$
) at 0.8 chord length, a deflection (
![]() $w_{te}/c$
) equal to 1% of the chord length at zero degrees is the most efficient configuration, as it achieves the highest
$w_{te}/c$
) equal to 1% of the chord length at zero degrees is the most efficient configuration, as it achieves the highest
![]() $C_{ l}/C_{d}$
and ensures the integrity of the morphing structure.
$C_{ l}/C_{d}$
and ensures the integrity of the morphing structure.
4.0 Conclusion
The current research extends the morphing aerofoil study from subsonic to transonic regime, which is the cruise condition for commercial aircraft. The goal of this research is to analyse the aerodynamic performance of various morphing aerofoil configurations and determine the most favourable shape. Critical validation for the cases was carried out with a GCI on three grids that proved the near grid independence result for the finer mesh. Experimental data from Harris [Reference Harris41] on the NACA0012 aerofoil at Mach = 0.8 and Re =
![]() $3 \times 10^6$
was used to validate the results. After considering the wall correction, the numerical results have good agreement with the experimental data. For the four angles of attack being validated, the largest error is
$3 \times 10^6$
was used to validate the results. After considering the wall correction, the numerical results have good agreement with the experimental data. For the four angles of attack being validated, the largest error is
![]() $5.4 \%$
for
$5.4 \%$
for
![]() $C_l$
, and
$C_l$
, and
![]() $12.3 \%$
for
$12.3 \%$
for
![]() $C_d$
.
$C_d$
.
To determine the optimal deflection and start position of the morphing part, the aerodynamic performance of 32 morphing configurations are analysed at four angles of attack. The optimal deflection
![]() $w_{te}$
of the morphing part is raging between
$w_{te}$
of the morphing part is raging between
![]() $1 \% $
and
$1 \% $
and
![]() $ 2.5 \%$
of the chord length. In fact, the impact of the deflection on
$ 2.5 \%$
of the chord length. In fact, the impact of the deflection on
![]() $C_l/C_d$
follow the same trend for the different starts of the morphing location considered.
$C_l/C_d$
follow the same trend for the different starts of the morphing location considered.
![]() $C_l/C_d$
will gradually increase with the deflection until an optimal value, and will then steadily decrease. The angle-of-attack impacts the efficiency the opposite way meaning that when it increases,
$C_l/C_d$
will gradually increase with the deflection until an optimal value, and will then steadily decrease. The angle-of-attack impacts the efficiency the opposite way meaning that when it increases,
![]() $C_l/C_d$
tends to decrease. Among these optimal deflections, the morphing aerofoil starting at
$C_l/C_d$
tends to decrease. Among these optimal deflections, the morphing aerofoil starting at
![]() $x_s/c=0.80$
is the most efficient. It is found that at this morphing configuration, the aerofoil is able to generate the highest
$x_s/c=0.80$
is the most efficient. It is found that at this morphing configuration, the aerofoil is able to generate the highest
![]() $C_l/C_d$
ratio. Furthermore, the shock wave location at this configuration is much further from the morphing part. It can be found at a minimum of 0.13 chord length away from the morphing part, ensuring that the zero Poisson’s ratio skin will be able to bear the flight conditions. From the study of
$C_l/C_d$
ratio. Furthermore, the shock wave location at this configuration is much further from the morphing part. It can be found at a minimum of 0.13 chord length away from the morphing part, ensuring that the zero Poisson’s ratio skin will be able to bear the flight conditions. From the study of
![]() $C_p$
and Mach contours for various deflection, it can be found that the shock wave formation is closely related to the angle-of-attack and deflection. It is found that the pressure gradient at the leading edge increases with the deflection of the aerofoil, and the position of the shock wave moves further downstream due to the decelerating effect caused by the morphing part. A positive pressure gradient can be found at the trailing edge as the deflection increases which contributes to the lift generation. Finally, the boundary layer detachment becomes more significant, when the angle-of-attack and the deflection increase.
$C_p$
and Mach contours for various deflection, it can be found that the shock wave formation is closely related to the angle-of-attack and deflection. It is found that the pressure gradient at the leading edge increases with the deflection of the aerofoil, and the position of the shock wave moves further downstream due to the decelerating effect caused by the morphing part. A positive pressure gradient can be found at the trailing edge as the deflection increases which contributes to the lift generation. Finally, the boundary layer detachment becomes more significant, when the angle-of-attack and the deflection increase.