No CrossRef data available.
Article contents
Accuracy of Küchemann’s prediction for the locus of aerodynamic centres on swept wings compared to an inviscid panel method
Published online by Cambridge University Press: 21 April 2022
Abstract
The locus of aerodynamic centres of a finite wing is the collection of all spanwise section aerodynamic centres, and depends on aspect ratio, wing sweep and planform shape. This locus is of great importance in the positioning of vortex elements in lifting-line theory. Traditionally, these vortex elements are placed along the quarter-chord of a wing, leading to inaccurate predictions of aerodynamic coefficients for swept wings due to the discontinuity in the line of vorticity at the wing root. An analytical solution was presented by Küchemann in 1956 to determine the locus of aerodynamic centres as a function of sweep. While experimental studies have been performed to visualise this locus, no large amount of data is available to fully evaluate the accuracy of Küchemann’s analytical solution. In the present study, a numerical approach is taken using a high-order panel method for inviscid, incompressible flow to calculate the locus of aerodynamic centres for elliptic wings over a wide range of sweep angles, aspect ratios and profile thicknesses. An inviscid panel method is chosen over full CFD solutions because of their ability to isolate the inviscid phenomena. Küchemann’s prediction is compared to this numerical data. The root mean square error is calculated for each wing in a broad design space to determine the accuracy of Küchemann’s theory. It is shown to be remarkably accurate over the range of cases studied, with the root mean square error staying below 4% for all wings with aft sweep and aspect ratios higher than
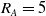$R_A=5$
. The actual difference between Küchemann’s prediction and numerical data is lower than that for the majority of the span for many of the wing designs considered, with the RMS error being skewed by the results at the tip. Results demonstrate that Küchemann’s analytical equations can be used as an accurate approximation for the locus of aerodynamic centres and could be used in modern numerical lifting-line algorithms*.
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Royal Aeronautical Society
Footnotes
*
This manuscript was previously published and presented by Moorthamers [1] at AIAA SciTech 2020 Forum in Orlando, Florida. Some statements have been slightly reworded.
References
Moorthamers, B. and Hunsaker, D.F. “Accuracy of Küchemann’s prediction for the locus of aerodynamic centres on swept wings,” AIAA SciTech 2020 Forum, Orlando, Florida, 2020.Google Scholar
Phillips, W. and Snyder, D. “Modern adaptation of Prandtl’s classic lifting-line theory,” J Aircr, 2000, 37, (4), pp 662–670.CrossRefGoogle Scholar
Prandtl, L. “Tragflügel Theorie,” Nachrichten von der Gesellschaft der Wisseschaften zu Göttingen, 1918, pp 451–477.Google Scholar
Marks, C.R., Zientarski, L., Culler, A.J., Hagen, B., Smyers, B.M. and Joo, J.J. “Variable camber compliant wing - Wind tunnel testing,” 23rd AIAA/AHS Adaptive Structures Conference, 2015, p 1051.Google Scholar
Joo, J.J., Marks, C.R., Zientarski, L. and Culler, A.J. “Variable camber compliant wing - Design,” 23rd AIAA/AHS Adaptive Structures Conference, Kissimmee, Florida, 2015 a, p 1050.Google Scholar
Miller, S.C., Rumpfkeil, M.P. and Joo, J.J. “Fluid-structure interaction of a variable camber compliant wing,” 53rd AIAA Aerospace Sciences Meeting, Kissimmee, Florida, 2015, p 1235.Google Scholar
Joo, J.J., Marks, C.R. and Zientarski, L. “Active wing shape reconfiguration using a variable camber compliant wing system,” 20th International Conference on Composite Materials, Copenhagen, 2015 b, p 12.Google Scholar
Marks, C.R., Zientarski, L. and Joo, J.J. “Investigation into the effect of shape deviation on variable camber compliant wing performance,” 24th AIAA/AHS Adaptive Structures Conference, 2016, p 1313.Google Scholar
Kudva, J., Appa, K., Martin, C., Jardine, A., Sendeckyj, G., Harris, T., et al., “Design, fabrication, and testing of the DARPA/Wright lab ‘Smart wing’ wind tunnel model,” 38th Structures, Structural Dynamics, and Materials Conference, 1997, p 1198.Google Scholar
Hetrick, J., Osborn, R., Kota, S., Flick, P. and Paul, D. “Flight testing of mission adaptive compliant wing,” 48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, 2007, p 1709.CrossRefGoogle Scholar
Vos, R., Gurdal, Z. and Abdalla, M. “Mechanism for warp-controlled twist of a morphing wing,” J Aircr., 2010, 47, (2), pp 450–457.CrossRefGoogle Scholar
Kuchemann, D. “A simple method for calculating the span and chordwise loading on straight and swept wings of any given aspect ratio at subsonic speed.” Tech. rep., Aeronautical Research Council London, 1956.Google Scholar
Boltz, F.W. and Kolbe, C.D. “The forces and pressure distribution at subsonic speeds on a cambered and twisted wing having 45 of sweepback, an aspect ratio of 3, and a taper ratio of 0.5,” NACA RMA52D22, 1952.Google Scholar
Hall, I. and Rogers, E. “Experiments with a tapered sweptback wing of warren 12 planform at mach numbers between 0.6 and 1.6,” RM-3271, Aeronautical Research Council, London, 1962.Google Scholar
Graham, R.R. “Low-speed characteristics of a 45 sweptback wing of aspect ratio 8 from pressure distributions and force tests at Reynolds numbers from 1,500,000 to 4,800,000,” NACA RM-L51H13, 1951.Google Scholar
Weber, J. and Brebner, G. “Low speed tests on a 45-deg swept Back wings, Part-I: Pressure measurements on wings of aspect ratio 5,” RM-2882, Aeronautical Research Council, London, 1958.Google Scholar
Phillips, W., Hunsaker, D.F. and Niewoehner, R. “Estimating the subsonic aerodynamic centre and moment components for swept wings,” J Aircr., 2008, 45, (3) a, pp 1033–1043.CrossRefGoogle Scholar
Magnus, A.E. and Epton, M.A. “PAN AIR: A computer program for predicting subsonic or supersonic linear potential flows about arbitrary configurations using a higher order panel method. Volume 1: Theory document (version 1.1),” 1981.Google Scholar
Hahn, M. and Drikakis, D. “Implicit large-eddy simulation of swept-wing flow using high-resolution methods,” AIAA J, 2009, 47, (3), pp 618–630.CrossRefGoogle Scholar
Takeuchi, K., Matsushima, K., Kanazaki, M. and Kusunose, K. “CFD analysis on sweep angles of the leading and trailing edges of a wing in a supersonic flow,” Trans JSME (in Japanese), 2015, 81, (827), pp 15–00037.CrossRefGoogle Scholar
Thomas, J. and Miller, D. “Numerical comparisons of panel methods at subsonic and supersonic speeds,” 17th Aerospace Sciences Meeting, 1979, p 404.Google Scholar
Sytsma, H., Hewitt, B.L. and Rubbert, P. “A Comparison of panel methods for subsonic flow computation,” Tech. Rep. AGARD-AG-241, Advisory Group for Aerospace Research and Development Neilly-sur-Seine, 1979.Google Scholar
Thomas, J., Luckring, J. and Sellers, III, W. “Evaluation of factors determining the accuracy of linearized subsonic panel methods,” Applied Aerodynamics Conference, 1983, p 1826.Google Scholar
Moorthamers, B. and Hunsaker, D.F. “Aerodynamic centre at the root of swept, elliptic wings in inviscid flow,” AIAA Scitech 2019 Forum, American Institute of Aeronautics and Astronautics, San Diego, California, 2019.Google Scholar
Phillips, W., Alley, N. and Niewoehner, R. “Effects of nonlinearities on subsonic aerodynamic centre,” J Aircr., 2008, 45, (4) b, pp 1244–1255.Google Scholar
Kuchemann, D. “The distribution of lift over the surface of swept wings,” Aeronaut Q, 1953, IV, pp 437–444.Google Scholar
Torenbeek, E. Advanced Aircraft Design: Conceptual Design, Analysis and Optimization of Subsonic Civil Airplanes. John Wiley & Sons, 2013.Google Scholar