Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-08T07:47:13.659Z Has data issue: false hasContentIssue false
  • English
  • Français

Theoretical lower limits of forebody drag

Published online by Cambridge University Press:  04 July 2016

Thomas Morel
Thomas Morel*
Affiliation:
Fluid Dynamics Research Department, General Motors Research Laboratories, Warren, Michigan
Get access Rights & Permissions [Opens in a new window]

Extract

One of the more important objectives of research in aerodynamics is drag reduction. In this paper we consider one part of the drag problem, the forebody pressure drag, and enquire about the lower limit to which it may theoretically be reduced by elimination of flow separation. It is customary to decompose the total drag force into two parts: pressure drag and friction drag, represented by force coefficients CD and CF, respectively. The ratio of these two forces may be taken as a convenient criterion to decide whether a body is ‘streamlined’ or ‘bluff’:

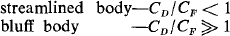
At high enough Reynolds numbers many bodies of interest are (according to this definition) bluff bodies, i.e. their pressure drag is much larger than the friction drag. This analysis is most relevant for bluff bodies where one needs to be concerned only with the pressure drag.

Type
Technical Notes
Information
The Aeronautical Journal , Volume 83 , Issue 817 , January 1979 , pp. 23 - 27
Copyright
Copyright © Royal Aeronautical Society 1979 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Arie, M. and Rouse, H. Experiments on two-dimensional flow over a normal wall. Journal of Fluid Mechanics, Vol 1, pp 129–141, 1956.10.1017/S0022112056000093Google Scholar
2. Prandtl, L. and Tietjens, O. Applied Hydro and Aeromechanics. Dover, pp 118–121, 1934.Google Scholar
3. Fail, R., Lawford, J. A. and Eyre, R. C. W. Low speed experiments on the wake characteristics of flat plates normal to an air stream. ARC R & M No 3120, June 1957.Google Scholar
4. Fage, A. Experiments on a sphere at critical Reynolds numbers. ARC R & M No 1766, 1936.Google Scholar
5. Batchelor, G. K. An Introduction to Fluid Dynamics. Cambridge University Press, p 340, 1967.Google Scholar