Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-23T11:42:14.211Z Has data issue: false hasContentIssue false
  • English
  • Français

A Multi-Line Standardless Method for X-Ray Powder Diffraction Phase Analysis

Published online by Cambridge University Press:  06 March 2019

D.Y. Li  and
B.H. O'Connor
D.Y. Li
Affiliation:
Department of Applied Physics Curtin University of Technology Perth, WA, Australia
B.H. O'Connor
Affiliation:
Department of Applied Physics Curtin University of Technology Perth, WA, Australia
Get access

Abstract

Quantitative phase analysis (QPA) methods which employ only one diffraction line for each phase arc generally unreliable due to the influence of systematic errors such as preferred orientation and extinction. Gazzara and Messier (1977) proposed a multi-line QPA method using normalised line intensities for line j of phase i,

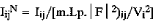
where Iij = measured Bragg intensity, m = multiplicity, Lp = Lorentz-polarisation factor, |F| = structure amplitude and Vi = cell volume. The method proposed here is a refinement of the Gazzara-Messier procedure. Phase compositions are calculated directly from the mean normalised Intensity 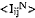for resolved lines which span the 2θ range of the instrument. The method makes use of the variance in 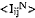to estimate standard deviations for the phase compositions. Test results are given for binaries of corundum-quartz and corundum-ceria.

Type
II. Quantitative Phase Analysis by X-Ray Diffraction (XRD)
Information
Advances in X-Ray Analysis , Volume 35 , Issue A: First Pacific-International Congress on X-ray Analytical Methods (PICXAM). Fortieth Annual Conference on Applications of X-ray Analysis, August 7-16, 1991 , 1991 , pp. 105 - 110
Copyright
Copyright © International Centre for Diffraction Data 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Klug, H.P. and Alexander, L. E. “X-ray Diffraction Procedures for Polycrystalline and Amorphous Materials” 2nd ed. Wiley-Interscience, p5 104, 367,541.Google Scholar
2. Hubbard, C.R., Evans, E.H. and Smith, D.K., 1976. J. Appl. Cryst. 9: 169.Google Scholar
3. Gazzara, C.P. and Messier, D.R., 1977. Ceramic Bulletin 56: 777.Google Scholar
4. O'Connor, B.H., and Chang, W.J, 1986. X-ray Spect. 15: 267.Google Scholar
5. Hill, R.J. and Howard, C.J., 1986. “A Computer Program for Rietveld Analysis of Fixed Wavelength X-ray and Neutron Powder Diffraction Patterns”. Australian Atomic Energy Commission.Google Scholar
6. Lewis, J., Swarzenbach, D. and Flach, H.D., 1982. Acta Cryst. A38 : 733.Google Scholar
7. Page, Y.L. and Donnay, G., 1976. Acta Cryst. B32: 2456.Google Scholar
8. Megaw, H.D. (1973). “Crystal Structures : A Working Approach”. W.R. Saunders and Co. : Philadelphia.Google Scholar
9. B.H., O'Connor and Raven, M.D., 1988. Powder Diffraction 3: 2.Google Scholar
10. Smith, D.K., Johnson, G.G. Jr., Scheible, A., Wims, A.M., Johnson, J.L., and Ullman, G., 1987. Powder Diffraction 2: 73.Google Scholar