Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-23T11:54:25.492Z Has data issue: false hasContentIssue false
  • English
  • Français

A Mathematical Comparison of the Lachance - Traill Matrix Correction Procedure with Statistical Multiple Linear Regression Analysis in XRF Applications

Published online by Cambridge University Press:  06 March 2019

Anthony J. Klimasara
Anthony J. Klimasara*
Affiliation:
GTE Electrical Products, Technical Assistance Laboratory, Danvers, MA 01923
Get access

Abstract

It will be shown that the Lachance-Traill XRF matrix correction equations can be derived from the statistical multiple linear regression model. By selecting and properly transforming the independent variables and then applying the statistical multiple linear regression model, the following form of the matrix correction equation is obtained:

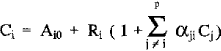
Furthermore, it will be shown that the Lachance-Traill influence coefficients have a deeper mathematical meaning. They can be related to the multiple regression coefficients of the transformed system:

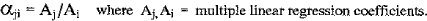
Finally, it will be proposed that the Lachance-Traill model is equivalent to the statistical multiple linear regression model with the transformed independent variables. Knowing these facts will simplify correction subroutines in Quantitative/Empirical XRF Analysis programs. These mathematical facts have already been implemented and presented in a paper: “Automated Quantitative XRF Analysis Software in Quality Control Applications” (Pacific-International Congress on X-ray Analytical Methods, Hawaii, 1991).

This demonstrates that the Lachance-Traill model has a strong mathematical foundation and is naturally justified mathematically.

Type
I. Mathematical Techniques in X-Ray Spectrometry
Information
Advances in X-Ray Analysis , Volume 36: Forty-First Annual Conference on Applications of X-ray Analysis, August 3-7, 1992 , 1992 , pp. 1 - 10
Copyright
Copyright © International Centre for Diffraction Data 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Lachance, G.R., “Introduction to Alpha Coefficients”, Corporation Scientifique Claisse, Inc., Sainte-Foy, Quebec, 1986.Google Scholar
2. Tertian, R., Claisse, F., “Principles of Quantitative X-ray Fluorescence Analysis”, Heyden & Son Ltd., 1982.Google Scholar
3. Klimasara, A.J. “Automated Quantitative XRF Analysis Software in Quality Control Applications”, Vol. 35, Advances in X-ray Analysis, Plenum Publ. Corp., NY, 1992.Google Scholar
4. Chatterjee, S., Price, B., “Regression Analysis by Example”, John Wiley & Sons, NY, 1977.Google Scholar
5. Hintze, J.L., “Number Cruncher Statistical System “-version 5.01, Published by Dr. Jerry L. Hintze, Kaysville, Utah, October 1987.Google Scholar
6. Davies, O.L., Goldsmith, P. L., “Statistical Methods in Research and Production”, Longman, London & New York, 1984.Google Scholar
7. Dillon, W. R., Goldstein, M., “Multivariate Analysis - Methods and Applications”, John Wiley & Sons, NY, 1984.Google Scholar
8. Dowdy, S., Wearden, S., “Statistics for Research”, John Wiley & Sons, NY, 1983.Google Scholar
9. Daniel, C., Wood, F. S., “ Fitting Equations to Data” - Computer Analysis of Multifactor Data, John Wiley & Sons, NY, 1980.Google Scholar
10. Green, W.R. “Computer-Aided Data Analysis”, John Wiley & Sons, NY, 1985.Google Scholar
11. McKeown, G.P., V.J., Rayward-Smith, “Mathematics for Computing”, John Wiley & Sons, NY, 1977.Google Scholar
12. Maindonald, J.H., “Statistical Computations”, John Wiley & Sons, NY, 1984.Google Scholar
13. Jennings, A., “Matrix Computation for Engineers and Scientists”, John Wiley & Sons, NY, 1980.Google Scholar
14. Parks, R.G., “Quattro Pro for Scientific and Engineering Spreadsheets”, Springer-Verlag, NY, 1992.Google Scholar
15. Orvis, W.J., “1-2-3 for Scientists and Engineers”, SYBEX, 1987.Google Scholar
16. Mezei, L.M., “Practical Spreadsheet Statistics and Curve Fitting for Scientists and Engineers”, Prentice Hall, Englewood Clifs, NJ, 1990.Google Scholar
17. Kral, I.H., “The EXCEL Spreadsheet for Engineers and Scientists”, Prentice Hall, Englewood Clifs, NJ, 1992.Google Scholar