Published online by Cambridge University Press: 06 March 2019
X-ray, neutron or electron diffraction patterns of alloys with structural disorder (micro-crystalline, amorphous or liquid alloys) consist of few diffuserings or halos. The ratio Ia(K)/<f> 2, where Ia(K) is the elastically scattered intensity per atom, K = 4πsinθ/λ, and <f> is average scattering factor of the alloy, is the sum of the Laue monotonic scattering (<f2> - <f2>)/<f2>, the small angle scattering Is(K) and interference function I(K). For isotropic distribution of the atoms in the alloy, one can write:

and
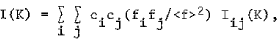
where
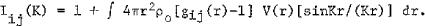
ρ0 is the average atomic density, V(r) is the size factor , ci and fi are the atomic concentration and atomic scattering factor of element i, respectively. Iij(K) is called the partial interference function which is related to the number ρij(r) = cjρ0gij(r) of j-type atoms per unit volume at the distancer from an i-type atom.
By varying the scattering factors of the elements through application of different radiations (x-rays, neutrons and electrons) and/or isotope enrichment, one can measure several I(K) which allow the evaluation of Iij(K) for a particular alloy. Assuming that gij(r) is independent of the relative abundance of the elements in the alloy , Iij(K) can also be obtained from several I(K) of the alloys with different concentratiora measured with a single radiation. This procedure has been applied to liquid Ag-Sn, Au-Sn and Cu-Sn alloys. The interference functions I(K), and their Fourier transforms, of vapor-quenched Ag-Ge and Ag-Cu films indicate that these alloys are micro polycrystalline with particle sizes of 15A in the Ag-52 at.% Cu alloy, 20A in the Ag-83 at.% Ge alloy and 24A in the Ag-64 at.% Ge alloy.