No CrossRef data available.
Article contents
A Simplified Method of Quantitating Preferred Orientation
Published online by Cambridge University Press: 06 March 2019
Abstract
Qualitative evaluation of preferred orientation in 10-rml Hastelloy N seamless tubing was carried out by obtaining conventional pole figures for several samples with the modified Schulz reflection technique. This established the texture as a (110)[112]. Quantitative determination of this texture was achieved for a large number of samples by a radial traverse of an azimuthally averaged (110) stereographic projection. This was accomplished with a Schulz goniometer by rotating the sample rapidly in its own plane while slowly varying the tilt angle ϕ. The first minimum observed in the resultant pattern approximates the pole density of the randomly oriented component of the sample. A scan obtained from a randomly oriented sample and suitably scaled to match pole density at these minima serves to distinguish the random from the oriented component of the sample. A ratio of the oriented to the random component as a function of the tilt angle ϕ is independent of the instrumental effects of defocusing and absorption. This ratio is proportional to the pole density of the oriented component since the pole density of the random component is a constant by definition. The same constant of proportionality yields a pole density of unity for the random component. Integrating the pole density for die random component over the surface of a reference sphere of unit radius gives the value 4π for the number of randomly oriented poles NR. The number of poles corresponding to the oriented component is obtained by evaluating the integral
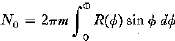
In this equation, R(ϕ) is the ratio of the oriented to the random component, Φ is the tilt angle corresponding to the first minimum in the sample scan, and m is a multiplicity factor which compensates for integration over just one 110 face of each grain. Evaluation of this integral may be made by plotting it with the aid of a family of sine curves and measuring the area under the curve.
The per cent of volume of the oriented component is then calculated by the relationship
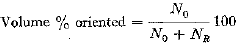
This method entails about 30min of an analyst's time and 40 to 120 min of machine time, depending on the grain size of the sample. Further information on the angular breadth of the texture may be obtained from the plot of the integrand. This technique is subject to the limitations that the material have a single texture and it must be possible tc prepare the specimens so that a suitably chosen pole figure contains a central concentration of poles which are delineated from other regions of pole concentration by a surrounding minimum in pole density. This is generally not too difficult in the case of sheet textures but requires that the specimen normal be parallel to ths fiber axis for a fiber texture.
- Type
- Research Article
- Information
- Copyright
- Copyright © International Centre for Diffraction Data 1967


