Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T02:42:44.296Z Has data issue: false hasContentIssue false
  • English
  • Français

Diffraction Analysis of Liquid and Amorphous Alloys

Published online by Cambridge University Press:  06 March 2019

C. N. J. Wagner
C. N. J. Wagner*
Affiliation:
Hammond Laboratory, Yale University New Haven, Connecticut 06520
Get access

Abstract

X-ray, neutron or electron diffraction patterns of alloys with structural disorder (micro-crystalline, amorphous or liquid alloys) consist of few diffuserings or halos. The ratio Ia(K)/<f> 2, where Ia(K) is the elastically scattered intensity per atom, K = 4πsinθ/λ, and <f> is average scattering factor of the alloy, is the sum of the Laue monotonic scattering (<f2> - <f2>)/<f2>, the small angle scattering Is(K) and interference function I(K). For isotropic distribution of the atoms in the alloy, one can write:

and

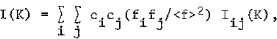
where

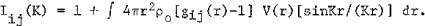
ρ0 is the average atomic density, V(r) is the size factor , ci and fi are the atomic concentration and atomic scattering factor of element i, respectively. Iij(K) is called the partial interference function which is related to the number ρij(r) = cjρ0gij(r) of j-type atoms per unit volume at the distancer from an i-type atom.

By varying the scattering factors of the elements through application of different radiations (x-rays, neutrons and electrons) and/or isotope enrichment, one can measure several I(K) which allow the evaluation of Iij(K) for a particular alloy. Assuming that gij(r) is independent of the relative abundance of the elements in the alloy , Iij(K) can also be obtained from several I(K) of the alloys with different concentratiora measured with a single radiation. This procedure has been applied to liquid Ag-Sn, Au-Sn and Cu-Sn alloys. The interference functions I(K), and their Fourier transforms, of vapor-quenched Ag-Ge and Ag-Cu films indicate that these alloys are micro polycrystalline with particle sizes of 15A in the Ag-52 at.% Cu alloy, 20A in the Ag-83 at.% Ge alloy and 24A in the Ag-64 at.% Ge alloy.

Type
Research Article
Information
Advances in X-Ray Analysis , Volume 12: Seventeenth Annual Conference on Applications of X-ray Analysis, August 21-23, 1968 , 1968 , pp. 50 - 71
Copyright
Copyright © International Centre for Diffraction Data 1968

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Mader, S., “Metastable Alloy Films”, J. Vac. Sci. Techn., 2, 35–41, 1965.Google Scholar
2. Kagner, C. N. J., Light, T. B., Haider, N. C., and Lukens, W. E., “Structure of a Vapor-Quenched AgCu Film”, J. Appl. Phys. (in press).Google Scholar
3. Duwez, P. and Willens, R. H., “Rapid Quenching of Liquid Alloys”, Trans. Met. Soc. AIME, 227, 362–365, 1963.Google Scholar
4. Fournet, G., “Etude de la Structure des Fluides et des Substances Amorphes au moyen de la Diffusion des Rayons X”, in S. Flügge, Editor, Encyclopedia of Physics, Vol. 32, Springer Verlag, Berlin, 1957, p. 238–320.Google Scholar
5. Kaplow, R., Strong, S. L. and Averhach, B. L., “Local Order in Liquid Alloys”, in J. B. Cohen and J. E. Hilliard, Editors, Local Atomic Arrangements Studied by X-Ray Diffraction, Gordon and Breach, Science Publishers, New York, 1966, p. 159–177.Google Scholar
6. Kagner, C. N. J. and Haider, N. C., “Atomic Distribution and Electronic Transport Properties in Liquid Alloys Studied by X-Ray Diffraction”, Adv. Physics, 16, 241–261, 1967.Google Scholar
7. Warren, B. E., “X-Ray Studies of Deformed Metals”, in B. Chalmers, Editor, Progress in Metal Physics, Vol. 8, Pergamon Press, London, 1959, p. 147–202.Google Scholar
8. Wagner, C. N. J., “Analysis of the Broadening and Changes in Position of Peaks in an X-Ray Powder Pattern”, in J. B. Cohen and J. E. Hilliard, Editors, Local Atomic Arrangements Studied by X-Ray Diffraction, Gordon and Breach, Science Publishers, New York, 1966, p. 219–269.Google Scholar
9. Joshi, M. L. and Wagner, C. N. J., “Atomic Distribution in Molten Silver-Tin Alloys”, Z. Naturf., 20a. 564–571, 1965.Google Scholar
10. North, D. M. and Wagner, C. N. J., “ Partial Interference Functions of Liquid Cu-Sn Alloys”, (to be published).Google Scholar
11. Orton, B. R., “An X-Ray Diffraction Study of Certain Pure Liquid Metals and Alloys for Evidence of the Covalent Bond”, Ph.D. Thesis, University of London, 1964.Google Scholar
12. Light, T. B. and Wagner, C. N. J., “The Structures of Vapor-Quenched Ag-Ge Films”, J. Appl. Cryst. (in press).Google Scholar
13. Guinier, A., “X-Ray Diffraction”, W. H. Freeman and Company, San Francisco, 1963.Google Scholar
14. Hosemann, R. and Bagchi, S. N., “Direct Analysis of Diffraction by Matter”, North Holland Publishing Company, Amsterdam, 1962.Google Scholar
15. Faber, T. E. and Ziman, J. M., “A Theory of the Electrical Properties of Liquid Metals. III. The Resistivity of Binary Alloys”, Phil. Mag., 11, 153–173, 1965.Google Scholar
16. Pings, C. J. and Waser, J., “Analysis of Scattering Data for Mixtures of Amorphous Solids or Liquids”, J. Chem. Phys., 48, 3016–3018, 1968.Google Scholar
17. Warren, B. E., Krutter, H. and Morningstar, O., “Fourier Analysis of X-Ray Patterns of Vitreous SiO2 and B2O3”, J. Am. Ceram. Soc, 19, 202–206, 1936.Google Scholar
18. Keating, D. T., “ Interpretation of the Neutron or X-Ray Scattering from a Liquid-Like Binary”, J. Appl. Phys., 34, 923–925, 1963.Google Scholar
19. Enderby, J. E., North, D. M. and Egelstaff, P. A., “The Partial Structure Factors in Liquid Cu-Sn”, Phil. Mag., 14, 961–970, 1966.Google Scholar
20. Kaplow, R. and Averbach, B. L., “X-Ray Diffractometer for the Study of Liquid Structures”, Rev. Sci. Instr., 34, 579–581, 1963.Google Scholar
21. Wagner, C. N. J., Ocken, H. and Joshi, M. L., “interference and Radial Distribution Functions of Liquid Copper, Silver, Tin and Mercury”, Z. Naturf., 20a, 325–335, 1965.Google Scholar
22. Levy, H. A., Danford, M. D. and Narten, A. H., “Data Collection and Evaluation with an X-Ray Diffractometer designed for the Study of Liquid Structure”, ORNL Report No. 3960. (Chemistry)Google Scholar
23. Joshi, M. L., “High Temperature Furnace for X-Ray Diffraction of Liquid Metals”, Rev. Sci. Instr., 36, 678–681, 1965.Google Scholar
24. Cromer, D. I. and Mann, J. B., “Compton Scattering Factors for Spherically Symmetric Free Atoms”, J. Chem. Phys., 47, 1892–1893, 1967.Google Scholar
25. Haider, N. C., Metzger, R. J. and Wagner, C. H. J., “Atomic Distribution and Electrical Properties of Liquid Mercury-Thallium Alloys”, J. Chem. Phys., 45, 1259–1268, 1966.Google Scholar
26. Cromer, D. T. and Waber, J. T., “Scattering Factors Computed from Relativistic Dirac-Slater Wave Functions”, Acta Cryst., 18, 104–109, 1965.Google Scholar
27. Hanson, H. P., Herman, F., Lea, J. D., and Skilman, S., “HFS Atomic Scattering Factors”, Acta Cryst., 17, 1040–1044, 1964.Google Scholar
28. Cromer, D. T., “Anomalous Dispersion Corrections Computed from Self-Consistent Field Relativistic Dirac-Slater Wave Functions”, Acta Cryst., 18, 17–23, 1965.Google Scholar
29. Vineyard, G. H., “The Theory and Structure of Liquids”, in Liquid Metals and Solidification, American Society for Metals, Cleveland, Ohio, 1958, p. 1-48.Google Scholar
30. Haider, N. C. and Wagner, C. N. J., “ Partial Interference and Atomic Distribution Functions of Liquid Silver-Tin Alloys”, J. Chem. Phys., 47, 4385–4391, 1967.Google Scholar
31. Wagner, C. N. J., Haider, N. C. and North, D. M., “ Partial Interference Functions of Liquid Gold-Tin Alloys”, Phys. Let., 25A, 663–664, 1967.Google Scholar
32. Ashcroft, N. W. and Langreth, D. C., “Structure of Binary Liquid Mixtures I”, Phys. Rev., 156, 685–692, 1967.Google Scholar
33. Enderby, J. E. and North, D. M., “Percus-Yevick Structure Factors for Liquid Alloys”, Phys. Chem. Liquids, 1, 1–11, 1968.Google Scholar
34. Piggott, M. R., “Resolution of Diffraction Rings by X-Rays and Electrons”, J. Appl. Physics, 37, 2927, 1966.Google Scholar
35. Germer, L. H. and White, A. H., “Electron Diffraction Studies of Thin Filits. II. Anomalous Powder Patterns Produced by Small Crystals”, Phys. Rev., 60, 447–454, 1941.Google Scholar
36. Grigson, C. W. B. and Barton, E., “The Development of the Face Centered Cubic Interference Functions as Crystals Grow”, Brit. J. Appl. Phys., 18, 175–183, 1967.Google Scholar
37. Ruppersberg, H., “Über die Atomverteilungskurven von einatomigen echten Metallen im festen und geschraolzenen Zustand”, Dr. rer. nat. habil. thesis, University of the Saar, Saarbrucken, Germany, 1967.Google Scholar