Published online by Cambridge University Press: 01 July 2016
Let Xn,…,X1 be independent, identically distributed (i.i.d.) random variables with distribution function F. A statistician, knowing F, observes the X values sequentially and is given two chances to choose Xs using stopping rules. The statistician's goal is to stop at a value of X as small as possible. Let 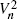 equal the expectation of the smaller of the two values chosen by the statistician when proceeding optimally. We obtain the asymptotic behaviour of the sequence
equal the expectation of the smaller of the two values chosen by the statistician when proceeding optimally. We obtain the asymptotic behaviour of the sequence 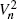 for a large class of Fs belonging to the domain of attraction (for the minimum) 𝒟(Gα), where Gα(x) = [1 - exp(-xα)]1(x ≥ 0) (with 1(·) the indicator function). The results are compared with those for the asymptotic behaviour of the classical one-choice value sequence
for a large class of Fs belonging to the domain of attraction (for the minimum) 𝒟(Gα), where Gα(x) = [1 - exp(-xα)]1(x ≥ 0) (with 1(·) the indicator function). The results are compared with those for the asymptotic behaviour of the classical one-choice value sequence 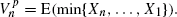 , as well as with the ‘prophet value’ sequence
, as well as with the ‘prophet value’ sequence 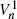
Supported by the Israel Science Foundation (grant number 879/01).