Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-03T04:11:53.949Z Has data issue: false hasContentIssue false
  • English
  • Français

Trace inequalities for mixtures of Markov chains

Published online by Cambridge University Press:  01 July 2016

Burton Singer  and
Seymour Spilerman
Burton Singer
Affiliation:
Columbia University, New York
Seymour Spilerman
Affiliation:
Russell Sage Foundation, New York
Get access Rights & Permissions [Opens in a new window]

Abstract

In a wide variety of multi-wave panel studies in economics and sociology, comparisons between the observed transition matrices and predictions of them based on time-homogeneous Markov chains have revealed a special kind of discrepancy: the trace of the observed matrices tends to be larger than the trace of the predicted matrices. A common explanation for this discrepancy has been via mixtures of Markov chains.

Specializing to mixtures of Markov semi-groups of the form

we exhibit classes of stochastic matrices M, probability measures µ and time intervals Δ such that 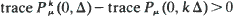for k = 2, 3 and 4. These examples contradict the substantial literature which suggests — implicitly — that the above inequality should be reversed for general mixtures of Markov semi-groups.

Keywords

MIXTUREMARKOV CHAINTRACE INEQUALITIESSOCIOLOGYPANEL STUDY
Type
Research Article
Information
Advances in Applied Probability , Volume 9 , Issue 4 , December 1977 , pp. 747 - 764
Copyright
Copyright © Applied Probability Trust 1977 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Bartholomew, D. J. (1973) Stochastic Models for Social Processes, 2nd edn. Wiley, New York.Google Scholar
[2] Blumen, I., Kogan, M. and McCarthy, P. J. (1955) The Industrial Mobility of Labor as a Probability Process. Cornell University Press, Ithaca, N.Y. Google Scholar
[3] Boudon, R. (1973) Mathematical Structures of Social Mobility. American Elsevier, New York.Google Scholar
[4] Coleman, J. S. (1964) Models of Change and Response Uncertainty. Prentice-Hall, Englewood Cliffs, N.J. Google Scholar
[5] Frank, R. (1962) Brand choice as a probability process. J. Business 35, 43–56.CrossRefGoogle Scholar
[6] Karpelewitsch, F. I. (1951) On the characteristic roots of a matrix with non-negative elements (in Russian). Izv. Akad. Nauk SSSR Ser. Mat. 15, 361–383.Google Scholar
[7] Mahoney, T. A. and Milkovich, G. T. (1971) The internal labor market as a stochastic process. In Manpower and Management Science, ed. Bartholomew, D. J. and Smith, A. R., Heath, D. C., Lexington, Mass., 75–92.Google Scholar
[8] McCall, J. J. (1973) Income Mobility, Racial Discrimination, and Economic Growth. D. C. Heath, Lexington, Mass.Google Scholar
[9] Mirsky, L. (1963) Results and problems in the theory of doubly-stochastic matrices. Z. Wahrscheinlichkeitsth. 1, 319–334.Google Scholar
[10] Morgan, J. N. and Smith, J. D. (1969) A Panel Study of Income Dynamics. Institute for Social Research, Ann Arbor, Mich. Google Scholar
[11] Parnes, H. S. (1975) Sources and uses of panels of microdata — the national longitudinal surveys: new vistas for labor market research. Amer. Econom. Rev. 65, 244–249.Google Scholar
[12] Perfect, H. (1952) On positive stochastic matrices with real characteristic roots. Proc. Camb. Phil. Soc. 48, 271–276.Google Scholar
[13] Perfect, H. (1953) Methods of constructing certain stochastic matrices, I. Duke Math. J. 20, 395–404.CrossRefGoogle Scholar
[14] Perfect, H. (1955) Methods of constructing certain stochastic matrices, II. Duke Math. J. 22, 305–311.Google Scholar
[15] Runnenberg, J. Th. (1962) On Elfving's problem of imbedding a time-discrete Markov chain in a continuous time one for finitely many states. Proc. Kon. Ned. Akad. Wetensch. A65, 536–541.CrossRefGoogle Scholar
[16] Scheffer, C. L. (1962) On Elfving's problem of embedding a time-discrete Markov chain in a time-continuous one for finitely many states, II. Proc. Kon. Ned. Akad. Wetensch. A65, 542–548.Google Scholar
[17] Singer, B. and Spilerman, S. (1974) Social mobility models for heterogeneous populations. In Sociological Methodology 1973–1974, ed. Costner, Herbert, Jossey-Bass, San Francisco, 356–401.Google Scholar
[18] Singer, B. and Spilerman, S. (1975) Identifying structural parameters of social processes using fragmentary data. Proceedings of the 40th Session of the ISI, Warsaw, Invited Papers 2, 681–697.Google Scholar
[19] Singer, B. and Spilerman, S. (1976) The representation of social processes by Markov models. Amer. J. Sociology 82, 1–54.CrossRefGoogle Scholar
[20] Singer, B. and Spilerman, S. (1976) Some methodological issues in the analysis of longitudinal surveys. Ann. Econom. Social Measurement 5, 447–474.Google Scholar
[21] Social Security Administration (1972) Basic statistical data files available to outside researchers. U. S. Department of Health, Education, and Welfare, (mimeo) Google Scholar
[22] Spilerman, S. (1972) Extensions of the mover-stayer model. Amer. J. Sociology 78, 599–627.Google Scholar
[23] Spilerman, S. (1972) The analysis of mobility processes by the introduction of independent variables into a Markov chain. Amer. Sociol. Rev. 37, 277–294.CrossRefGoogle Scholar
[24] Suleimanova, H. R. (1949) Stochastic matrices with real characteristic numbers. Dokl. Akad. Nauk SSSR 66, 343–345.Google Scholar