No CrossRef data available.
Published online by Cambridge University Press: 02 April 2024
In this paper we extend results on reconstruction of probabilistic supports of independent and identically distributed random variables to supports of dependent stationary 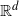 ${\mathbb R}^d$-valued random variables. All supports are assumed to be compact of positive reach in Euclidean space. Our main results involve the study of the convergence in the Hausdorff sense of a cloud of stationary dependent random vectors to their common support. A novel topological reconstruction result is stated, and a number of illustrative examples are presented. The example of the Möbius Markov chain on the circle is treated at the end with simulations.
${\mathbb R}^d$-valued random variables. All supports are assumed to be compact of positive reach in Euclidean space. Our main results involve the study of the convergence in the Hausdorff sense of a cloud of stationary dependent random vectors to their common support. A novel topological reconstruction result is stated, and a number of illustrative examples are presented. The example of the Möbius Markov chain on the circle is treated at the end with simulations.