Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-24T02:41:59.216Z Has data issue: false hasContentIssue false
  • English
  • Français

Sur Une Équation Fonctionnelle Et SES Applications: Une Extension Du Théorème De Kesten-Stigum Concernant Des Processus De Branchement

Part of: Special processes Markov processes

Published online by Cambridge University Press:  01 July 2016

Quansheng Liu
Quansheng Liu*
Affiliation:
Universit de Rennes 1
*
∗ Postal address: Institut Mathematique de Rennes, Universite de Rennes 1, Campus de Beaulieu, 35042 Rennes Cedex, France. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

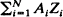Given a random integer N ≧ 0 and a sequence of random variables Ai ≧ 0, we define a transformation T on the class of probability measures on [0, ∞) by letting Tμ be the distribution of , where {Zi} are independent random variables with distribution μ, which are independent of N and of {Ai} as well. We obtain the optimal conditions for the functional equation μ = Tμ to have a non-trivial solution of finite mean, and we study the existence of moments of the solutions. The work unifies the corresponding theorems of Kesten-Stigum concerning the Galton-Watson process, of Biggins for branching random walks, of Kahane-Peyrière for a model of turbulence of Yaglom made precise by Mandelbrot, and of Durrett-Liggett for the study of invariant measures for certain infinite particle systems.

Keywords

BRANCHING PROCESSESBRANCHING RANDOM WALKSFUNCTIONAL EQUATIONMANDELBROT'S MARTINGALE

MSC classification

Primary: 60J80: Branching processes (Galton-Watson, birth-and-death, etc.)
Secondary: 60K35: Interacting random processes; statistical mechanics type models; percolation theory
Type
General Applied Probability
Information
Advances in Applied Probability , Volume 29 , Issue 2 , June 1997 , pp. 353 - 373
Copyright
Copyright © Applied Probability Trust 1997 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bibliographie

Asmussen, S. Et Hering, H. (1983) Branching Processes. Birkhäuser, Basel.CrossRefGoogle Scholar
Athreya, K. B. (1970) A simple proof of a result of Kesten and Stigum on supercritical multitype Galton-Watson branching processes. Ann. Math. Statist. 41, 195–202.CrossRefGoogle Scholar
Athreya, K. B. (1971) A note on a functional equation arising in Galton-Watson branching processes. J. Appl. Prob. 8, 589–598.CrossRefGoogle Scholar
Athreya, K. B. Et Ney, P. E. (1972) Branching Processes. Springer, Berlin.CrossRefGoogle Scholar
Athreya, K. B. Et Kaplan, N. (1976) Convergence of the age distribution in the one-dimensional supercritical age-independent branching processes. Ann. Prob. 4, 38–50.CrossRefGoogle Scholar
Ben Nasr, F. (1987) Mesures aléatoires de Mandelbrot associées à des substitutions. C.R. Acad. Sci. Paris 304, 255–258.Google Scholar
Biggins, J. D. (1977) Martingale convergence in the branching random walk. J. Appl. Prob. 14, 25–37.CrossRefGoogle Scholar
Biggins, J. D. (1979) Growth rates in the branching random walk. Z. Wahrscheinlichkeitsth. 48, 17–34.CrossRefGoogle Scholar
Biggins, J. D. (1992) Uniform convergence of martingales in the branching random walk. Ann. Prob. 20, 137–151.CrossRefGoogle Scholar
Bingham, N. H. Et Doney, R. A. (1974) Asymptotic properties of supercritical branching processes I: the Galton-Watson process. Adv. Appl. Prob. 6, 711–731.CrossRefGoogle Scholar
Bingham, N. H. Et Doney, R. A. (1975) Asymptotic properties of supercritical branching processes II: Crump-Mode and Jirina processes. Adv. Appl. Prob. 7, 66–82.CrossRefGoogle Scholar
Chauvin, B. Et Rouault, A. (1996) Boltzmann-Gibbs weights in the branching random walk. In Classical and Modern Branching Processes. (IMA Volumes in Mathematics and its Applications 84). ed. Athreya, K. B. and Jagers, P. Springer, New York. pp. 41–50.Google Scholar
Collet, P. Et Koukiou, F. (1992) Large deviations for multiplicative chaos. Commun. Math. Phys. 147, 329–342.CrossRefGoogle Scholar
Crump, K. Et Mode, C. J. (1968) A general age-dependent branching processes (I). J. Math. Anal. Appl. 24, 497–508.CrossRefGoogle Scholar
Crump, K. Et Mode, C. J. (1969) A general age-dependent branching processes (II). J. Math. Anal. Appl. 25, 8–17.CrossRefGoogle Scholar
Doney, R. A. (1972) A limit theorem for a class of supercritical branching processes. J. Appl. Prob. 9, 707–724.CrossRefGoogle Scholar
Doney, R. A. (1973) On a functional equation for general branching processes. J. Appl. Prob. 10, 198–205.CrossRefGoogle Scholar
Durrett, R. Et Liggett, Th. (1983) Fixed points of the smoothing transformation. Z. Wahrscheinlichkeitsth. 64, 275–301.CrossRefGoogle Scholar
Falconer, K. J. (1986) Random fractals. Math. Proc. Camb. Phil. Soc. 100, 559–582.CrossRefGoogle Scholar
Falconer, K. J. (1987) Cut-set sums and tree processes. Math. Proc. Amer. Math. Soc. 101, 337–346.CrossRefGoogle Scholar
Falconer, K. J. (1994) The multifractal spectrum of statistically self-similar measures. J. Theoret. Prob. 7, 681–702.CrossRefGoogle Scholar
Fortet, R. et Mourier, E. (1953) Ann. Scient. Ecole Normale Sup. 70, 266–285.Google Scholar
Franchi, J. (1993) Chaos multiplicatif: Un traitement simple et complet de la fonction de partition. Prépublication 148. Laboratoire de Probabilités de l'Université Paris VI.Google Scholar
Graf, S., Mauldin, R. D. Et Williams, S. C. (1988) The exact Hausdorff dimension in random recursive constructions. Mem. Amer. Math. Soc. 71, 381.Google Scholar
Guivarc'H, Y. (1990) Sur une extension de la notion de loi semi-stable. Ann. Inst. Henri Poincaré 26, 261–285.Google Scholar
Harris, T. E. (1948) Branching processes. Ann. Math. Statist. 19, 474–494.CrossRefGoogle Scholar
Holley, R. and Liggett, Th. (1981) Generalized potlatch and smoothing processes. Z. Wahrscheinlichkeitsth. 55, 165–195.CrossRefGoogle Scholar
Holley, R, and Waymire, E. C. (1992) Multifractal dimensions and scaling exponents for strongly bounded random cascades. Ann. Appl. Prob. 2, 819–845.CrossRefGoogle Scholar
Kahane, J. P. (1987) Multiplications aléatoires et dimensions de Hausdorff. Ann. Inst. Henri Poincaré 23, 289–296.Google Scholar
Kahane, J. P. Et Peyriere, J. (1976) Sur certaines martingales de Benoit Mandelbrot. Adv. Math. 22, 131–345.CrossRefGoogle Scholar
Liu, Q. (1993) Sur quelques problèmes à propos des processus de branchement, des flots dans les réseaux et des mesures de Hausdorff associées. Thèse. Université Paris 6.Google Scholar
Liu, Q. (1998) Fixed points of a generalized smoothing transformation and applications to the branching random walk. Adv. Appl. Prob. 30 to appear.CrossRefGoogle Scholar
Mandelbrot, B. (1974a) Multiplications aléatoires et distributions invariantes par moyenne pondérée aléatoire. C.R. Acad. Sci. Paris 278, 289–292.Google Scholar
Mandelbrot, B. (1974b) Multiplications aléatoires et distributions invariantes par moyenne pondérée aléatoire: quelques extensions. C.R. Acad. Sci. Paris 278, 355–358.Google Scholar
Mauldin, R. D. and Williams, S. C. (1986) Random constructions, asymptotic geometric and topological properties. Trans. Amer. Math. Soc. 295, 325–346.CrossRefGoogle Scholar
Neveu, J. (1972) Martingales à Temps Discret. Masson, Paris.Google Scholar
Peyriere, J. (1977) Calculs de dimensions de Hausdorff. Duke Math. J. 44, 591–601.CrossRefGoogle Scholar
Royer, G. (1984) Distance de Fortet-Mourier et fonctions log-concaves. Ann. Sci. de Clermont-Ferrand 78.Google Scholar
Waymire, E. C. Et Williams, S. C. (1994) A general decomposition theory for random cascades. Bull. Amer. Math. Soc. 31, 216–222.CrossRefGoogle Scholar
Waymire, E. C. Et Williams, S. C. (1995) Multiplicative cascades: dimension spectra and dependence. J. Fourier Anal. Appl. (Special issue in honour of J.-P. Kahane.) pp. 489–609.Google Scholar
Waymire, E. C. Et Williams, S. C. (1996) A cascade decomposition theory with applications to Markov and exchangeable cascades. Trans. Amer. Math. Soc. 348, 585–632.CrossRefGoogle Scholar
Waymire, E. C. Et Williams, S. C. (1996) Markov cascades. In Classical and Modern Branching Processes. (IMA Volumes in Mathematics and its Applications 84). ed. Athreya, K. B. and Jagers, P. Springer, New York. pp. 305–321.Google Scholar