Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T19:42:35.176Z Has data issue: false hasContentIssue false
  • English
  • Français

The supremum distribution of a Lévy process with no negative jumps

Published online by Cambridge University Press:  01 July 2016

J. Michael Harrison
J. Michael Harrison*
Affiliation:
Stanford University
Get access Rights & Permissions [Opens in a new window]

Abstract

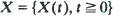Let be a process with stationary, independent increments and no negative jumps. Let 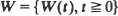be this same process modified by a reflecting barrier at zero (a storage process). Assuming that – 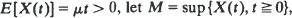and denote by ψ(s) the exponent function of X. A simple formula is derived for the Laplace transform of 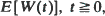as a function of W(0). Using the fact that the distribution of M is the unique stationary distribution of the Markov process W, this yields an elementary proof that the Laplace transform of M is µs/ψ(s). If 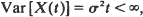it follows that 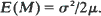These surprisingly simple formulas were originally obtained by Zolotarev using analytical methods.

Keywords

STATIONARY INDEPENDENT INCREMENTSSTORAGE PROCESSESMARKOV PROCESSESREFLECTING BARRIERSLÉVY PROCESSES
Type
Research Article
Information
Advances in Applied Probability , Volume 9 , Issue 2 , June 1977 , pp. 417 - 422
Copyright
Copyright © Applied Probability Trust 1977 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bingham, N. H. (1975) Fluctuation theory in continuous time. Adv. Appl. Prob. 7, 705–766.Google Scholar
Breiman, L. (1968) Probability. Addison–Wesley, Reading, Mass.Google Scholar
Gani, J. and Prabhu, N. U. (1960) The content of a dam as the supremum of an infinitely divisible process. J. Math. Mech. 9, 639–651.Google Scholar
Pecherskii, E. A. and Rogozin, B. A. (1969) On joint distributions of random variables associated with fluctuations of a process with independent increments. Theory Prob. Appl. 14, 410–423.CrossRefGoogle Scholar
Takács, L. (1967) Combinatorial Methods in the Theory of Stochastic Processes. Wiley, New York.Google Scholar
Zolotarev, V. M. (1964) The first passage time of a level and the behavior at infinity for a class of processes with independent increments. Theory Prob. Appl. 9, 653–662.Google Scholar