No CrossRef data available.
Published online by Cambridge University Press: 01 September 2023
We consider an SIR (susceptible 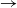 $\to$ infective
$\to$ infective 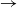 $\to$ recovered) epidemic in a closed population of size n, in which infection spreads via mixing events, comprising individuals chosen uniformly at random from the population, which occur at the points of a Poisson process. This contrasts sharply with most epidemic models, in which infection is spread purely by pairwise interaction. A sequence of epidemic processes, indexed by n, and an approximating branching process are constructed on a common probability space via embedded random walks. We show that under suitable conditions the process of infectives in the epidemic process converges almost surely to the branching process. This leads to a threshold theorem for the epidemic process, where a major outbreak is defined as one that infects at least
$\to$ recovered) epidemic in a closed population of size n, in which infection spreads via mixing events, comprising individuals chosen uniformly at random from the population, which occur at the points of a Poisson process. This contrasts sharply with most epidemic models, in which infection is spread purely by pairwise interaction. A sequence of epidemic processes, indexed by n, and an approximating branching process are constructed on a common probability space via embedded random walks. We show that under suitable conditions the process of infectives in the epidemic process converges almost surely to the branching process. This leads to a threshold theorem for the epidemic process, where a major outbreak is defined as one that infects at least 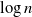 $\log n$ individuals. We show further that there exists
$\log n$ individuals. We show further that there exists 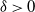 $\delta \gt 0$, depending on the model parameters, such that the probability that a major outbreak has size at least
$\delta \gt 0$, depending on the model parameters, such that the probability that a major outbreak has size at least 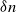 $\delta n$ tends to one as
$\delta n$ tends to one as 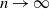 $n \to \infty$.
$n \to \infty$.