Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-22T22:48:21.807Z Has data issue: false hasContentIssue false
  • English
  • Français

Storage processes with general release rule and additive inputs

Published online by Cambridge University Press:  01 July 2016

P. J. Brockwell ,
S. I. Resnick  and
R. L. Tweedie
P. J. Brockwell*
Affiliation:
Colorado State University
S. I. Resnick*
Affiliation:
Colorado State University
R. L. Tweedie
Affiliation:
CSIRO Division of Mathematics and Statistics, Melbourne
*
∗Postal address: Department of Statistics, Colorado State University, Fort Collins, CO 80523, U.S.A.
∗Postal address: Department of Statistics, Colorado State University, Fort Collins, CO 80523, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Abstract

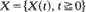A construction is given of a process in which X(t) represents the content at time t of a dam whose cumulative input process 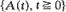is a Lévy process with measure v and whose release rate at time t is r(X(t)). It is assumed only that r(0) = 0 and that r is strictly positive and left-continuous with strictly positive finite right limits on (0,∞). The sample-paths of X are shown to satisfy the storage equation

The process X is analyzed using renewal theory and stochastic comparison techniques, and necessary and sufficient conditions are found in terms of v and r for X to have a stationary distributionπ. These generalize previous results which were obtained under the assumption that v is finite. Conditions for Πto have an atom at 0 are considered in some detail, and related results on the positivity of the expected occupation time of level 0 are given.

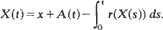
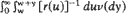Necessary and sufficient conditions for the existence of Πare expressed in terms of the existence of non-negative integrable solutions of certain integral equations and conditions are given under which such solutions are necessarily stationary densities for X. A simple sufficient condition for X to have a stationary distribution is found in terms of and in the case when r is non-decreasing the condition is shown to be also necessary. Finally some examples are considered; these show that the results described above unify various known conditions in special cases, and confirm several conjectures in the related literature.

Keywords

DAM THEORYSTORAGE EQUATIONSTATIONARY DISTRIBUTIONLÉVY PROCESSGENERAL RELEASE RULEMARKOV PROCESS
Type
Research Article
Information
Advances in Applied Probability , Volume 14 , Issue 2 , June 1982 , pp. 392 - 433
Copyright
Copyright © Applied Probability Trust 1982 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research supported by NSF Grant MCS 78-00915-01.

a

Present address: SIROMATH Pty Ltd, 1 York St., Sydney, NSW 2000, Australia.

References

Athreya, K. B. and Ney, P. E. (1972) Branching Processes. Springer-Verlag, Berlin.Google Scholar
Arjas, E., Nummelin, E. and Tweedie, R. L. (1978) Uniform limit theorems for non-singular renewal and Markov renewal processes. J. Appl. Prob. 15, 112–125.Google Scholar
Billingsley, P. (1968) Convergence of Probability Measures. Wiley, New York.Google Scholar
Breiman, L. (1968) Probability. Addison-Wesley, Reading, MA.Google Scholar
Brockwell, P. J. (1977) Stationary distributions for dams with additive input and content-dependent release rate. Adv. Appl. Prob. 9, 645–663.Google Scholar
Brockwell, P. J. and Chung, K. L. (1975) Emptiness times of a dam with stable input and general release rule. J. Appl. Prob. 12, 212–217.Google Scholar
ÇInlar, E. (1975a) A local time for a storage process. Ann. Prob. 3, 930–951.CrossRefGoogle Scholar
ÇInlar, E. (1975b) Introduction to Stochastic Processes. Prentice-Hall, Englewood Cliffs, NJ.Google Scholar
ÇInlar, E. and Pinsky, M. (1971) A stochastic integral in storage theory. Z. Wahrscheinlichkeitsth. 2, 180–224.Google Scholar
ÇInlar, E. and Pinsky, M. (1972) On dams with additive inputs and a general release rule. J. Appl. Prob. 9, 422–429.CrossRefGoogle Scholar
Harrison, J. M. and Resnick, S. I. (1976) The stationary distribution and first exit probabilities of a storage process with general release rule. Math. Operat. Res. 1, 347–358.CrossRefGoogle Scholar
Harrison, J. M. and Resnick, S. I. (1978) The recurrence classification of risk and storage processes. Math. Operat. Res. 3, 57–66.CrossRefGoogle Scholar
Ito, K. (1969) Stochastic Processes. Lecture Notes Series No. 16, Matematisk Institut, Aarhus University.Google Scholar
Kingman, J. F. C. (1963) On continuous time models in the theory of dams. J. Austral. Math. Soc. 3, 480–487.CrossRefGoogle Scholar
Miller, D. R. (1972) Existence of limits in regenerative processes. Ann. Math. Statist. 43, 1275–1282.CrossRefGoogle Scholar
Petrovski, I. G. (1966) Ordinary Differential Equations. Prentice-Hall, Englewood Cliffs, NJ.Google Scholar
Pratt, J. (1960) On interchanging limits and integrals. Ann. Math. Statist. 31, 74–77.Google Scholar
Rubinovitch, M. and Cohen, J. W. (1980) Level crossings and stationary distributions for general dams. J. Appl. Prob. 17, 218–226.CrossRefGoogle Scholar
Shtatland, E. S. (1965) On local properties of processes with independent increments. Theory Prob. Appl. 10, 317–322.Google Scholar
Tuominen, P. and Tweedie, R. L. (1979) Exponential ergodicity in Markovian queueing and dam models. J. Appl. Prob. 16, 867–880.Google Scholar
Yeo, G. F. (1976) A dam with general release rule. J. Austral. Math. Soc., B19, 469–477.Google Scholar