Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-27T00:17:13.406Z Has data issue: false hasContentIssue false
  • English
  • Français

Stationary representation of queues. I

Published online by Cambridge University Press:  01 July 2016

Władysław Szczotka
Władysław Szczotka*
Affiliation:
Wrocław University
*
∗Postal address: Mathematical Institute, Wrodaw University, PI. Grunwaldzki 2/4, 50-384 Wrodaw, Poland
Get access Rights & Permissions [Opens in a new window]

Abstract

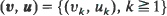The paper deals with the asymptotic behaviour of queues for which the generic sequence is not necessarily stationary but is asymptotically stationary in some sense. The latter property is defined by an appropriate type of convergence of probability distributions 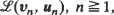of the sequences 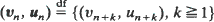to the distribution 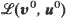of a stationary sequence 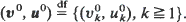We consider six types of convergence of 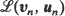to

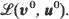
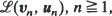The main result is as follows: if the sequence of the distributions converges in one of six ways then the sequence of distributions 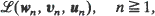of the sequences 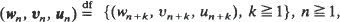converges in the same way, independently of initial conditions. Furthermore the limiting distribution is the same as the limiting distribution obtained by the weak convergence of the distributions 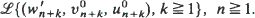Here wk and w∗k denote the waiting time of the kth unit in the queue generated by (v, u) and (v0, u0) respectively.

Keywords

FIFO SINGLE-SERVER QUEUEWAITING TIMEQUEUE SIZEASYMPTOTIC STATIONARITY
Type
Research Article
Information
Advances in Applied Probability , Volume 18 , Issue 3 , September 1986 , pp. 815 - 848
Copyright
Copyright © Applied Probability Trust 1986 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Billingsley, P. (1968) Convergence of Probability Measures. Wiley, New York.Google Scholar
2. Borovkov, A. A. (1972) Stochastic Processes in Queueing Theory (in Russian). Nauka, Moscow.Google Scholar
3. Lindvall, T. (1973) Weak convergence of probability measures and random functions in function space D[0, 8). J. Appl. Prob. 10, 109–121.CrossRefGoogle Scholar
4. Loynes, R. M. (1962) The stability of a queue with non-independent inter-arrival and service times. Proc. Camb. Phil. Soc. 58, 497–520.Google Scholar
5. Rolski, T. (1981) Queue with non-stationary input stream: Ross&s conjecture. Adv. Appl. Prob. 13, 603–618.Google Scholar
6. Szczotka, W. (1979) Factorization of the distribution of waiting time. Zast. Mat. XVI, 395–403.Google Scholar
7. Szczotka, W. (1986) Joint distribution of waiting time and queue size for single server queue. Dissertationes Math. 248.Google Scholar
8. Szczotka, W. (1986) Stationary representation of queue II. Adv. Appl. Prob. 18, 849–859.Google Scholar