We study a model for the destruction of a random network by fire. Suppose that we are given a multigraph of minimum degree at least 2 having real-valued edge lengths. We pick a uniform point from along the length and set it alight; the edges of the multigraph burn at speed 1. If the fire reaches a vertex of degree 2, the fire gets directly passed on to the neighbouring edge; a vertex of degree at least 3, however, passes the fire either to all of its neighbours or none, each with probability 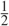${\textstyle{1 \over 2}}$. If the fire goes out before the whole network is burnt, we again set fire to a uniform point. We are interested in the number of fires which must be set in order to burn the whole network, and the number of points which are burnt from two different directions. We analyse these quantities for a random multigraph having n vertices of degree 3 and α(n) vertices of degree 4, where α(n)/n → 0 as n → ∞, with independent and identically distributed standard exponential edge lengths. Depending on whether 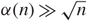$\alpha(n) \gg \sqrt{n}$ or 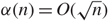$\alpha(n)=O(\sqrt{n})$, we prove that, as n → ∞, these quantities converge jointly in distribution when suitably rescaled to either a pair of constants or to (complicated) functionals of Brownian motion. We use our analysis of this model to make progress towards a conjecture of Aronson, Frieze and Pittel (1998) concerning the number of vertices which remain unmatched when we use the Karp–Sipser algorithm to find a matching on the Erdős–Rényi random graph.