Published online by Cambridge University Press: 01 July 2016
For point processes, such that the interarrival times of points are independently and identically distributed, let T(L, m) denote the time until at least 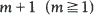 points cluster within an interval of length at most L. Let τ (L, m) + 1 be the total number of points observed until the above happens. Simple approximations of Eτ (L, m) and ET(L, m) are derived, as well as lower and upper bounds for their value. Approximations to the variances are also given. In particular the Poisson, Bernoulli and compound Poisson processes are discussed in detail. Some numerical tables are included.
points cluster within an interval of length at most L. Let τ (L, m) + 1 be the total number of points observed until the above happens. Simple approximations of Eτ (L, m) and ET(L, m) are derived, as well as lower and upper bounds for their value. Approximations to the variances are also given. In particular the Poisson, Bernoulli and compound Poisson processes are discussed in detail. Some numerical tables are included.
This research was done while the author spent a sabbatical year at Columbia and Rutgers Universities.