Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T14:39:36.251Z Has data issue: false hasContentIssue false
  • English
  • Français

Set Reconstruction by Voronoi Cells

Part of: Combinatorial probability Geometric probability and stochastic geometry Stochastic processes General convexity

Published online by Cambridge University Press:  04 January 2016

M. Reitzner ,
E. Spodarev  and
D. Zaporozhets
M. Reitzner*
Affiliation:
Universität Osnabrück
E. Spodarev*
Affiliation:
Universität Ulm
D. Zaporozhets*
Affiliation:
V. A. Steklov Mathematical Institute
*
∗ Postal address: Institut für Mathematik, Universität Osnabrück, 49069 Osnabrück, Germany. Email address: [email protected]
∗∗ Postal address: Institut für Stochastik, Universität Ulm, 89069 Ulm, Germany. Email address: [email protected]
∗∗∗ Postal address: St. Petersburg Department, V. A. Steklov Mathematical Institute, Fontanka 27, 191023 St. Petersburg, Russia. Email address: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a Borel set A and a homogeneous Poisson point process η in 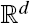of intensity λ>0, define the Poisson–Voronoi approximation Aη of A as a union of all Voronoi cells with nuclei from η lying in A. If A has a finite volume and perimeter, we find an exact asymptotic of E Vol(AΔ Aη) as λ→∞, where Vol is the Lebesgue measure. Estimates for all moments of Vol(Aη) and Vol(AΔ Aη) together with their asymptotics for large λ are obtained as well.

Keywords

Poisson point processPoisson–Voronoi cellPoisson–Voronoi tessellationperimeter

MSC classification

Primary: 60D05: Geometric probability and stochastic geometry
Secondary: 60G55: Point processes 52A22: Random convex sets and integral geometry 60C05: Combinatorial probability
Type
Stochastic Geometry and Statistical Applications
Information
Advances in Applied Probability , Volume 44 , Issue 4 , December 2012 , pp. 938 - 953
Copyright
© Applied Probability Trust 

Footnotes

Partially supported by RFBR (10-01-00242), NSh-4472.2010.1, RFBR-DFG (09-0191331), and DFG (436 RUS 113/962/0-1 R) grants.

References

Ambrosio, L., Colesanti, A. and Villa, E. (2008). Outer Minkowski content for some classes of closed sets. Math. Ann. 342, 727–748.CrossRefGoogle Scholar
Ambrosio, L., Fusco, N. and Pallara, D. (2000). Functions of Bounded Variation and Free Discontinuity Problems. Oxford University Press, New York.Google Scholar
Averkov, G. and Bianchi, G. (2009). Confirmation of Matheron's conjecture on the covariogram of a planar convex body. J. Europ. Math. Soc. 11, 1187–1202.CrossRefGoogle Scholar
Billingsley, P. (1979). Probability and Measure. John Wiley, New York.Google Scholar
Einmahl, J. H. J. and Khmaladze, E. V. (2001). The two-sample problem in R m and measure-valued martingales. In State of the Art in Probability and Statistics (Leiden, 1999; IMS Lecture Notes Monogr. Ser. 36), Institute of Mathematical Statistics, Beachwood, OH, pp. 434–463.CrossRefGoogle Scholar
Galerne, B. (2011). Computation of the perimeter of measurable sets via their covariogram. Applications to random sets. Image Anal. Stereol. 30, 39–51.Google Scholar
Heveling, M. and Reitzner, M. (2009). Poisson–Voronoi approximation. Ann. Appl. Prob. 19, 719–736.Google Scholar
Khmaladze, E. and Toronjadze, N. (2001). On the almost sure coverage property of Voronoi tessellation: the R1 case. Adv. Appl. Prob. 33, 756–764.CrossRefGoogle Scholar
Last, G. and Penrose, M. D. (2011). Poisson process Fock space representation, chaos expansion and covariance inequalities. Prob. Theory Relat. Fields 150, 663–690.Google Scholar
Møller, J. (1994). Lectures on Random Voronoı˘ Tessellations (Lecture Notes Statist. 87). Springer, New York.CrossRefGoogle Scholar
Penrose, M. D. (2007). Laws of large numbers in stochastic geometry with statistical applications. Bernoulli 13, 1124–1150.Google Scholar
Schneider, R., and Weil, W. (2008). Stochastic and Integral Geometry. Springer, Berlin.Google Scholar
Schulte, M. (2012). A central limit theorem for the Poisson–Voronoi approximation. Adv. Appl. Math. 49, 285–306.CrossRefGoogle Scholar
Stoyan, D., Kendall, W. S. and Mecke, J. (1995). Stochastic Geometry and Its Applications, 2nd edn. John Wiley, Chichester.Google Scholar
Wu, L. (2000). A new modified logarithmic Sobolev inequality for Poisson point processes and several applications. Prob. Theory Relat. Fields 118, 427–438.CrossRefGoogle Scholar