Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-23T18:44:48.904Z Has data issue: false hasContentIssue false
  • English
  • Français

A Self-Normalized Central Limit Theorem for Markov Random Walks

Part of: Markov processes Limit theorems

Published online by Cambridge University Press:  04 January 2016

Cheng-Der Fuh  and
Tian-Xiao Pang
Cheng-Der Fuh*
Affiliation:
National Central University
Tian-Xiao Pang*
Affiliation:
Zhejiang University
*
∗ Postal address: Graduate Institute of Statistics, National Central University, Jhongli, Taiwan. Email address: [email protected]
∗∗ Postal address: Department of Mathematics, Zhejiang University, Hangzhou 310027, P. R. China. Email address: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Motivated by the study of the asymptotic normality of the least-squares estimator in the (autoregressive) AR(1) model under possibly infinite variance, in this paper we investigate a self-normalized central limit theorem for Markov random walks. That is, let {Xn, n ≥ 0} be a Markov chain on a general state space X with transition probability P and invariant measure π. Suppose that an additive component Sn takes values on the real line 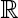, and is adjoined to the chain such that {Sn, n ≥ 1} is a Markov random walk. Assume that Sn = ∑k=1nξk, and that {ξn, n ≥ 1} is a nondegenerate and stationary sequence under π that belongs to the domain of attraction of the normal law with zero mean and possibly infinite variance. By making use of an asymptotic variance formula of Sn / √n, we prove a self-normalized central limit theorem for Sn under some regularity conditions. An essential idea in our proof is to bound the covariance of the Markov random walk via a sequence of weight functions, which plays a crucial role in determining the moment condition and dependence structure of the Markov random walk. As illustrations, we apply our results to the finite-state Markov chain, the AR(1) model, and the linear state space model.

Keywords

Self-normalizedcentral limit theoremMarkov random walkPoisson equationdomain of attraction of the normal law

MSC classification

Primary: 60F05: Central limit and other weak theorems
Secondary: 60J25: Continuous-time Markov processes on general state spaces
Type
General Applied Probability
Information
Advances in Applied Probability , Volume 44 , Issue 2 , June 2012 , pp. 452 - 478
Copyright
© Applied Probability Trust 

References

Anderson, T. W. (1959). On asymptotic distributions of estimates of parameters of stochastic difference equations. Ann. Math. Statist. 30, 676–687.Google Scholar
Basawa, I. V. and Prakasa Rao, B. L. S. (1980). Statistical Inference for Stochastic Processes. Academic Press, London.Google Scholar
Bentkus, V. and Götze, F. (1996). The Berry-Esseen bound for Student's statistic. Ann. Prob. 24, 491–503.Google Scholar
Bertail, P. and Clémençon, S. (2006). Regeneration-based statistics for Harris recurrent Markov chains. In Dependence in Probability and Statistics (Lecture Notes Statist. 187), Springer, New York, pp. 3–54.Google Scholar
Billingsley, P. (1999). Convergence of Probability Measures, 2nd edn. John Wiley, New York.CrossRefGoogle Scholar
Bingham, N. H., Goldie, C. M. and Teugels, J. L. (1989). Regular Variation. Cambridge University Press.Google Scholar
Bolthausen, E. (1982). The Berry-Esseén theorem for strongly mixing Harris recurrent Markov chains. Z. Wahrscheinlichkeitsth. 60, 283–289.Google Scholar
Bradley, R. C. (1988). A central limit theorem for stationary ρ-mixing sequences with infinite variance. Ann. Prob. 16, 313–332.CrossRefGoogle Scholar
Brockwell, P. J. and Davis, R. A. (1991). Time Series: Theory and Methods, 2nd edn. Springer, New York,Google Scholar
Chen, X. (1999). The law of the iterated logarithm for functionals of Harris recurrent Markov chains: self-normalization. J. Theoret. Prob. 12, 421–445.Google Scholar
Chow, Y. S. and Teicher, H. (1998). Probability Theory, Independence, Interchangeability, Martingales. Springer, New York.Google Scholar
Csörgő, M., Lin, Z. Y. and Shao, Q. M. (1994). Studentized increments of partial sums. Sci. China A 37, 265–276.Google Scholar
Csörgő, M., Szyszkowicz, B. and Wang, Q. (2003a). Darling-Erdös theorem for self-normalized sums. Ann. Prob. 31, 676–692.Google Scholar
Csörgő, M., Szyszkowicz, B. and Wang, Q. (2003b). Donsker's theorem for self-normalized partial sums processes. Ann. Prob. 31, 1228–1240.Google Scholar
De la Peña, V. H., Lai, T. L. and Shao, Q.-M. (2009). Self-Normalized Processes. Springer, Berlin.Google Scholar
Diebold, F. X. and Inoue, A. (2001). Long memory and regime switching. J. Econometrics 105, 131–159.Google Scholar
Faure, M. (2002). Self-normalized large deviations for Markov chains. Electron. J. Prob. 7, 31pp.Google Scholar
Fuh, C.-D. (2006). Efficient likelihood estimation in state space models. Ann. Statist. 34, 2026–2068.CrossRefGoogle Scholar
Fuh, C.-D. and Hu, I. (2007). Estimation in hidden Markov models via efficient importance sampling. Bernoulli 13, 492–513.Google Scholar
Fuh, C.-D. and Zhang, C.-H. (2000). Poisson equation, moment inequalities and quick convergence for Markov random walks. Stoch. Process Appl. 87, 53–67.Google Scholar
Giné, E., Götze, F. and Mason, D. M. (1997). When is the Student t-statistic asymptotically standard normal? Ann. Prob. 25, 1514–1531.Google Scholar
Griffin, P. S. and Kuelbs, J. D. (1989). Self-normalized laws of the iterated logarithm. Ann. Prob. 17, 1571–1601.Google Scholar
Hall, P. and Seneta, E. (1988). Products of independent, normally attracted random variables. Prob. Theory Relat. Fields 78, 135–142.Google Scholar
Jing, B.-Y., Shao, Q.-M. and Wang, Q. (2003). Self-normalized Cramér-type large deviations for independent random variables. Ann. Prob. 31, 2167–2215.Google Scholar
Kulik, R. (2006). Limit theorems for self-normalized linear processes. Statist. Prob. Lett. 76, 1947–1947.Google Scholar
Lai, T. L. and Shao, Q.-M. (2007). Self-normalized limit theorems in probability and statistics. In Asymptotic Theory in Probability and Statistics with Applications, eds Lai, T. L., Qian, L. and Shao, Q.-M.. International Press, Somerville, MA, pp. 3–43.Google Scholar
Lifshits, B. A. (1978). On the central limit theorem for Markov chains. Theory Prob. Appl. 23, 279–296.CrossRefGoogle Scholar
Lin, Z. (1996). A self-normalized Chung-type law of the iterated logarithm. Theory Prob. Appl. 41, 791–798.Google Scholar
Maxwell, M. and Woodroofe, M. (2000). Central limit theorems for additive functionals of Markov chains. Ann. Prob. 28, 713–724.Google Scholar
McElroy, T. and Politis, D. (2007). Self-normalization for heavy-tailed time series with long memory. Statistica Sinica 17, 199–220.Google Scholar
Meyn, S. P. and Tweedie, R. L. (1993). Markov Chains and Stochastic Stability. Springer, London.Google Scholar
Nagaev, S. V. (1957). Some limit theorems for stationary Markov chains. Theory Prob. Appl. 2, 378–406.Google Scholar
Ney, P. and Nummelin, E. (1987). Markov additive processes. I. Eigenvalue properties and limit theorems. Ann. Prob. 15, 561–592.CrossRefGoogle Scholar
Nummelin, E. (1978). A splitting technique for Harris recurrent Markov chains. Z. Wahrscheinlichkeitsch. 43, 309–318.Google Scholar
Peligrad, M. and Shao, Q. M. (1994). Self-normalized central limit theorem for sums of weakly dependent random variables. J. Theoret. Prob. 7, 309–338.Google Scholar
Roussas, G. G. (1969a). Nonparametric estimation in Markov processes. Ann. Inst. Statist. Math. 21, 73–87.CrossRefGoogle Scholar
Roussas, G. G. (1969b). Nonparametric estimation of the transition distribution function of a Markov process. Ann. Math. Statist. 40, 1386–1400.Google Scholar
Shao, Q.-M. (1997). Self-normalized large deviations. Ann. Prob. 25, 285–328.Google Scholar