Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-25T00:59:23.340Z Has data issue: false hasContentIssue false
  • English
  • Français

Selective sweep and the size of the hitchhiking set

Part of: Markov processes Special processes

Published online by Cambridge University Press:  01 July 2016

Stephanie Leocard
Stephanie Leocard*
Affiliation:
Université de Provence
*
∗ Postal address: CMI, Technopôle Château-Gombert, 39 rue Joliot Curie, 13453 Marseille cedex 13, France. Email address: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Just after the fixation of an advantageous allele in the population (this spread is called a selective sweep), the neutral genes close to the site under selection tend to have the same ancestor as the gene under selection. However, some recombinations may occur during the selective sweep and break the link, which reduces the number of hitchhiking alleles. We consider a large selection coefficient α and extend the results of Etheridge, Pfaffelhuber and Wakolbinger (2006) and the work of Pfaffelhuber and Studeny (2007) about genetic hitchhiking, where the recombination rate scales with α/log α. We first describe the genealogy at an arbitrary number of partially linked neutral loci, with an order of accuracy of 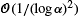in total variation. Then, we use this framework to obtain an approximate distribution for the size of the hitchhiking set at the end of the selective sweep, with the same accuracy.

Keywords

Coalescencerecombinationselective sweephitchhiking allele

MSC classification

Primary: 92D15: Problems related to evolution
Secondary: 60J80: Branching processes (Galton-Watson, birth-and-death, etc.) 60J85: Applications of branching processes 60K37: Processes in random environments 92D10: Genetics
Type
General Applied Probability
Information
Advances in Applied Probability , Volume 41 , Issue 3 , September 2009 , pp. 731 - 764
Copyright
Copyright © Applied Probability Trust 2009 

References

Depaulis, F. and Veuille, M. (1998). Neutrality tests based on the number of haplotypes under an infinite site model. Molec. Biol. Evol. 15, 1788–1790.Google Scholar
Etheridge, A., Pfaffelhuber, P. and Wakolbinger, A. (2006). An approximate sampling formula under genetic hitchhiking. Ann. Appl. Prob. 16, 685–729.Google Scholar
Ethier, S. N. and Kurtz, T. G. (1986). Markov Processes. John Wiley, New York.Google Scholar
Evans, S. N. and O'Connell, N. (1994). Weighted occupation time for branching particle systems and a representation for the supercritical superprocess. Canad. Math. Bull. 37, 187–196.Google Scholar
Griffiths, R. C. (2003). The frequency spectrum of a mutation and its age, in a general diffusion model. Theoret. Pop. Biol. 64, 241–251.CrossRefGoogle Scholar
Hanchard, N. et al. (2006). Screening for recently selected alleles by analysis of human haplotype similarity. Amer. J. Human Genet. 78, 153–159.Google Scholar
Hudson, R. et al. (1994). Evidence for positive selection in the superoxide dismutase (Sod) region of Drosophila melanogaster . Genetics 136, 1329–1340.Google Scholar
Kaj, I. and Krone, S. M. (2003). The coalescent process in a population with stochastically varying size. J. Appl. Prob. 40, 33–48.Google Scholar
Lehnert, A., Pfaffelhuber, P. and Stephan, W. (2008). Linkage disequilibrium under genetic hitchhiking in finite populations. Genetics 179, 527–537.Google Scholar
Maynard-Smith, J. and Haigh, J. (1974). The hitch-hiking effect of a favorable gene. Genet. Res. 23, 23–35.Google Scholar
McVean, G. (2007). The structure of linkage disequilibrium around a selective sweep. Genetics 175, 1395–1406.Google Scholar
O'Connell, N. (1993). Yule process approximation for the skeleton of a branching process. J. Appl. Prob. 30, 725–729.Google Scholar
Pfaffelhuber, P. and Studeny, A. (2007). Approximating genealogies for partially linked neutral loci under a selective sweep. J. Math. Biol. 55, 299–330.Google Scholar
Pfaffelhuber, P., Haubold, B. and Wakolbinger, A. (2006). Approximate genealogies under genetic hitchhiking. Genetics 174, 1995–1995.Google Scholar
Sabeti, P. C. et al. (2002). Detecting recent positive selection in the human genome from haplotype structure. Nature 419, 832–837.Google Scholar
Schweinsberg, J. and Durrett, R. (2005). Random partitions approximating the coalescence of lineages during a selective sweep. Ann. Appl. Prob. 15, 1591–1651.Google Scholar
Stephan, W., Song, Y. S. and Langley, C. H. (2006). The hitchhiking effect on linkage disequilibrium between linked loci. Genetics 172, 2647–2663.Google Scholar
Wang, E., Komada, G., Baldi, P. and Moyzis, R. (2006). Global landscape of recent inferred Darwinian selection for Homo sapiens . Proc. Nat. Acad. Sci. USA 103, 135–140.Google Scholar