Article contents
Second-order approximations for certain stopped sums in extended renewal theory
Published online by Cambridge University Press: 01 July 2016
Abstract
Let (X0, Y0), (X1, Y1), · ·· be a sequence of independent two-dimensional random vectors such that (X1, Y1), (X2, Y2), · ·· are i.i.d. Let {(Sn, Un)}n≧0 be the associated sum process, and define for t ≧ 0
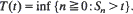 Under suitable conditions on (X0, Y0) and (X1, Y1) we derive expansions up to vanishing terms, as t→∞, for EUT(t), Var UT(t) and Cov (UT(t), T(t)). Corresponding results will be obtained for EUN(t), Var UN(t) and Cov (UN(t), N(t)) when X0, Χ1 are both almost surely non-negative and
Under suitable conditions on (X0, Y0) and (X1, Y1) we derive expansions up to vanishing terms, as t→∞, for EUT(t), Var UT(t) and Cov (UT(t), T(t)). Corresponding results will be obtained for EUN(t), Var UN(t) and Cov (UN(t), N(t)) when X0, Χ1 are both almost surely non-negative and
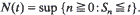
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Applied Probability Trust 1988
References
- 7
- Cited by


