Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-26T08:15:46.781Z Has data issue: false hasContentIssue false
  • English
  • Français

A rendezvous-evasion game on discrete locations with joint randomization

Part of: Operations research and management science

Published online by Cambridge University Press:  01 July 2016

Wei Shi Lim
Wei Shi Lim*
Affiliation:
National University of Singapore
*
*Postal address: Department of Decision Sciences, Faculty of Business Administration, National University of Singapore, 10 Kent Ridge Crescent, Singapore S119260.
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a problem proposed by S. Alpern (European Journal of Operational Research (1997)) of how two players can optimally rendezvous while at the same time evading an enemy searcher. This problem can be modelled as a two-person, zero-sum game between the rendezvous team R (with agents R1, R2) and the searcher S. This paper gives the first solution to such a rendezvous-evasion game by considering a version that is discrete in time and space, as in the pure rendezvous problem of Anderson and Weber (Journal of Applied Probability28, pp. 839–851). R1,R2 and S start at different locations among the n identical locations where there is no common labelling and at each integer time they may rellocate to any one of the n locations. When some location is occupied by more than one player, the game ends. If S is at this location, S (maximizer) wins and the payoff is 1; otherwise R(minimizer) wins and the payoff is 0. The value of the game is the probability that Swins under optimal play. We assume that R1 and R2 can jointly randomize their strategies. When n equals 3, the value of the game is 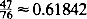. We also prove that the value of the game is bounded above by 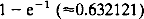asymptotically. If, in addition, the players share a common notion of a directed cycle containing all the nlocations (while still able to move between any two locations), the value of the game is ((1 – 2/n)n–1 + l)/2. Finally, we prove that with this extra information, R can secure a strictly lower value for all n.

Keywords

RENDEZVOUSSEARCHZERO-SUM GAME

MSC classification

Primary: 90B40: Search theory
Type
General Applied Probability
Information
Advances in Applied Probability , Volume 29 , Issue 4 , December 1997 , pp. 1004 - 1017
Copyright
Copyright © Probability Trust 1997 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Alpern, S. (1995) The rendezvous search problem. SIAM J. Control Optim. 33, 673–683.Google Scholar
[2] Alpern, S. and Asic, M. (1985) The search value of a network. Networks 15, 229–238.CrossRefGoogle Scholar
[3] Alpern, S. and Asic, M. (1986) Ambush strategies in search games on graphs. SIAM J. Control Optim. 24, 66–75.CrossRefGoogle Scholar
[4] Alpern, S. and Beck, A. (1997) Rendezvous search on the line with bounded resources. Europ. J. Operat. Res. (in press).Google Scholar
[5] Alpern, S. and Gal, S. (1995) Rendezvous search on the line with distinguishable players. SIAM J. Control Optim. 33, 1270–1276.Google Scholar
[6] Anderson, E. J. and Essegaier, S. (1995) Rendezvous search on the line with indistinguishable players. SIAM J. Control Optim. 33, 1637–1642.CrossRefGoogle Scholar
[7] Anderson, E. J. and Weber, R. R. (1990) The rendezvous problem on discrete locations. J. Appl. Prob. 28, 839–851.Google Scholar
[8] Gal, S. (1960) Search Games. Academic Press, New York.Google Scholar
[9] Gal, S. and Anderson, E. J. (1990) Search in a maze. Prob. Eng. Inf. Sci. 4, 311–318.Google Scholar
[10] Isaacs, R. (1965) Differential Games. Wiley, New York.Google Scholar
[11] Lim, W. S. (1996) Rendezvous-evasion as a multi-stage game with observed actions. LSE CDAM-Research Report Series 96–05.Google Scholar
[12] Lim, W. S., Beck, A. and Alpern, S. (1997) Rendezvous search on the line with more than two players. Operat. Res. 45, 357–364.Google Scholar
[13] Ruckle, W. H. (1983) Pursuit on a cyclic graph. Int. J. Game Theory 10, 91–99.CrossRefGoogle Scholar