Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-23T13:33:39.066Z Has data issue: false hasContentIssue false
  • English
  • Français

A ratio limit theorem for (sub) Markov chains on {1,2, …} with bounded jumps

Part of: Limit theorems Markov processes

Published online by Cambridge University Press:  01 July 2016

Harry Kesten
Harry Kesten*
Affiliation:
Cornell University
*
* Postal address: Department of Mathematics, White Hall, Cornell University, Ithaca, NY 14853–7901, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

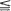We consider positive matrices Q, indexed by {1,2, …}. Assume that there exists a constant 1 L < ∞ and sequences u1< u2< · ·· and d1d2< · ·· such that Q(i, j) = 0 whenever i < ur < ur + L < j or i > dr + L > dr > j for some r. If Q satisfies some additional uniform irreducibility and aperiodicity assumptions, then for s > 0, Q has at most one positive s-harmonic function and at most one s-invariant measure µ. We use this result to show that if Q is also substochastic, then it has the strong ratio limit property, that is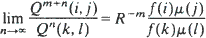

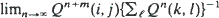for a suitable R and some R–1-harmonic function f and R–1-invariant measure µ. Under additional conditions µ can be taken as a probability measure on {1,2, …} and exists. An example shows that this limit may fail to exist if Q does not satisfy the restrictions imposed above, even though Q may have a minimal normalized quasi-stationary distribution (i.e. a probability measure µ for which R–1µ = µQ).

The results have an immediate interpretation for Markov chains on {0,1,2, …} with 0 as an absorbing state. They give ratio limit theorems for such a chain, conditioned on not yet being absorbed at 0 by time n.

Keywords

ABSORBING MARKOV CHAINUNIQUENESS OF HARMONIC FUNCTIONS AND HARMONIC MEASURESQUASI-STATIONARY DISTRIBUTION

MSC classification

Primary: 60J10: Markov chains (discrete-time Markov processes on discrete state spaces)
Secondary: 60F99: None of the above, but in this section 60J25: Continuous-time Markov processes on general state spaces
Type
General Applied Probability
Information
Advances in Applied Probability , Volume 27 , Issue 3 , September 1995 , pp. 652 - 691
Copyright
Copyright © Applied Probability Trust 1995 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research supported by the NSF through a grant to Cornell University.

References

Billingsley, P. (1986) Probability and Measure, 2nd edn. Wiley, New York.Google Scholar
Feller, W. (1968) An Introduction to Probability Theory and Its Applications, Vol. I, 3rd edn. Wiley, New York.Google Scholar
Ferrari, P. A., Martinez, S. and Picco, P. (1992) Existence of non trivial quasi-stationary distributions in the birth and death chain. Adv. Appl. Prob. 24, 795–813.Google Scholar
Ferrari, P. A., Kesten, H., Martinez, S. and Picco, P. (1995) Existence of quasi-stationary distributions. A renewal dynamical approach. Ann. Prob. 23. To appear.CrossRefGoogle Scholar
Folkman, J. H. and Port, S. C. (1966) On Markov chains with the strong ratio limit property. J. Math. Mech. 15, 113–122.Google Scholar
Freedman, D. (1983) Markov Chains. Springer-Verlag, New York.CrossRefGoogle Scholar
Gantmacher, F. R. (1959) The Theory of Matrices. Chelsea, New York.Google Scholar
Gnedenko, B. V. and Kolmogorov, A. N. (1968) Limit Theorems for Sums of Independent Random Variables, 2nd edn. Addison-Wesley, Reading, MA.Google Scholar
Good, Ph. (1968) The limiting behavior of transient birth and death processes conditioned on survival. J. Austral. Math. Soc. 8, 716–722 (see also Math. Rev. 39 (1970) #2224).CrossRefGoogle Scholar
Jacka, S. D. and Roberts, G. O. (1995) Weak convergence of conditioned processes on a countable state space. J. Appl. Prob. 32.Google Scholar
Karlin, S. and Mcgregor, J. L. (1957) The differential equations of birth and death processes and the Stieltjes moment problem. Trans. Amer. Math. Soc. 85, 489–546.Google Scholar
Karlin, S. and Mcgregor, J. (1959) Random walks. Ill. J. Math. 3, 66–81.Google Scholar
Kersting, G. (1974) Strong ratio limit property and R-recurrence of reversible Markov chains. Z. Wahrscheinlichkeitsth. 30, 343–356.Google Scholar
Kersting, G. (1976) A note on R-recurrence of Markov chains. Z. Wahrscheinlichkeitsth. 35, 355–358.CrossRefGoogle Scholar
Kesten, H. (1963) Ratio theorems for random walks (II). J. d'Anal. Math. 11, 323–379.Google Scholar
Kesten, H. and Spitzer, F. (1963) Ratio theorems for random walks (I). J. d'Anal. Math. 11, 285–322.Google Scholar
Kijima, M. (1992) On the existence of quasi-stationary distributions in denumerable R-transient Markov chains. J. Appl. Prob. 29, 21–36.CrossRefGoogle Scholar
Kijima, M. (1993) Correction to M. Kijima (1992), J. Appl. Prob. 30, 496.Google Scholar
Kingman, J. F. C. and Orey, S. (1964) Ratio limit theorems for Markov chains. Proc. Amer. Math. Soc. 15, 907–910.Google Scholar
Neveu, J. (1972) Martingales a Temps Discret. Masson, Paris.Google Scholar
Orey, S. (1961) Strong ratio limit property. Bull. Amer. Math. Soc. 67, 571–574.Google Scholar
Pakes, A. G. (1978) On the age distribution of a Markov chain. J. Appl. Prob. 15, 65–77.Google Scholar
Pakes, A. G. (1979) The age of a Markov process. Stoch. Proc. Appl. 8, 277–303.Google Scholar
Papangelou, F. (1967) Strong ratio limits, R-recurrence and mixing properties of discrete parameter Markov processes. Z. Wahrscheinlichkeitsth. 8, 259–297.CrossRefGoogle Scholar
Pruitt, W. E. (1965) Strong ratio limit property for R-recurrent Markov chains. Proc. Amer. Math. Soc. 16, 196–200.Google Scholar
Seneta, E. and Vere-Jones, D. (1966) On quasi-stationary distributions in discrete time Markov chains with a denumerable infinity of states. J. Appl. Prob. 3, 403–434.Google Scholar
Spitzer, F. (1956) A combinatorial lemma and its application to probability theory. Trans. Amer. Math. Soc. 82, 323–339.CrossRefGoogle Scholar
Van Doorn, E. A. (1991) Quasi-stationary distributions and convergence to quasi-stationarity of birth-death processes. Adv. Appl. Prob. 23, 683–700.Google Scholar
Van Doorn, E. A. and Schrijner, P. (1993) Random walk polynomials and random walk measures. J. Computational Appl. Math. 49, 289–296.CrossRefGoogle Scholar
Van Doorn, E. A. and Schrijner, P. (1995a) Ratio limits and limiting conditional distributions for discrete time birth-death processes. J. Math. Anal. Appl. 190, 263–284.Google Scholar
Van Doorn, E. A. and Schrijner, P. (1995b) Geometric ergodicity and quasi-stationarity in discrete time birth-death processes. J. Austral. Math. Soc. B 46.Google Scholar
Vere-Jones, D. (1967) Ergodic properties of nonnegative matrices I. Pacific J. Math. 22, 361–386.Google Scholar
Yaglom, A. M. (1947) Certain limit theorems for the theory of branching process. Dokl. Akad. Nauk SSSR 56, 795–798.Google Scholar